a)
 Funktionsgraphen zuordnen
Funktionsgraphen zuordnen
Um festzustellen, welcher Graph die Funktionsschar

für den Parameter

und

zeigt, betrachtest du zuerst die Unterschiede der beiden Graphen.
Eine „normale“

-Funktion verläuft monoton wachsend auf ganz

und besitzt den Ordinatenabschnitt

.
Betrachtest du den Term der Funktion

, lässt sich dieser schreiben als

.
Dies ist eine gebrochenrationale Funktion. Der Nenner, die

-Funktion, wächst dabei, wie du bereits weißt, monoton an. Der Funktionswert wird somit für steigende Argumente

kleiner.
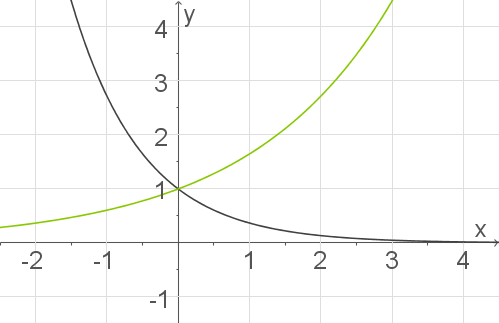
Der grüne Graph zeigt eine

-Funktion mit positivem Exponenten, in diesem Fall mit

. Der andere Graph fällt für steigende

-Werte und zeigt den Graph von

.

 -Koordinate berechnen
-Koordinate berechnen
Du sollst die Stelle bzw.

-Koordinate berechnen, bei welchem die Tangente an den Graphen von

die Steigung

besitzt.
Die Tangentensteigung ist allerdings immer gleich der Steigung der Funktion im Berührpunkt ihres Graphen.
Du berechnest somit die Stelle, an welcher

gilt.
1. Schritt: Funktion aufstellen und Ableitung berechnen
Um diese Gleichung zu lösen, benötigst du die Ableitung

. Die Funktion

lautet dabei:
![\(\begin{array}[t]{rll}
f_4(x)&=& \mathrm e^{4\cdot x} &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d6f019195afc88f199a1f1e278e091fb70b2e279e66723f15d3a9e21a1839cef_light.svg)
Die Ableitung bestimmst du mit der Kettenregel:
Dabei gilt

und

. Du erhälst die Funktionsgleichung der Ableitung:
![\(\begin{array}[t]{rll}
f_4‘(x)&=& 4\cdot\mathrm e^{4\cdot x} &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0a9766675e4e383b1225c5cbd58d2147c795437cd8d7775dfed53ec85eb88ca2_light.svg) 2. Schritt: Gleichung lösen
2. Schritt: Gleichung lösen
Mit dieser Funktionsgleichung löst du die Gleichung

, um die

-Koordinate zu bestimmen:
Die Tangente an den Graphen von

hat an der Stelle

die Steigung

.
 Orthogonalität nachweisen
Orthogonalität nachweisen
Gegeben sind die Tangenten

, welche den Graphen

im Punkt

berühren.
Du sollst nachweisen, dass es einen Parameter

gibt, sodass die zugehörige Tangente

, welche den Graphen im Punkt

berührt, die Tangente

senkrecht schneidet.
Aus der Aufgabenstellung weißt du, dass für zwei sich senkrecht schneidende Geraden und Tangenten mit den Steigungen

und

gilt:
1. Schritt: Steigung berechnen
Für die Steigungen der Tangenten benötigst du den Term der Ableitung, welchen du erneut mit der Kettenregel erhälst:
![\(\begin{array}[t]{rll}
f_k(x)&=& \mathrm e^{k\cdot x} &\\[5pt]
f_k‘(x)&=& k\cdot\mathrm e^{k\cdot x}
\end{array}\)](https://www.schullv.de/resources/formulas/2e2948a86e5cb520e47b36bfb1169155e92dc450631a3915a36cd79e971afa55_light.svg)
Im Punkt

, beziehungsweise an der Stelle

hat der Graph von

die Steigung:
![\(\begin{array}[t]{rll}
f_k‘(0)&=& k\cdot\mathrm e^{k\cdot 0} &\\[5pt]
&=& k\cdot 1 \\[5pt]
&=& k
\end{array}\)](https://www.schullv.de/resources/formulas/121d8e6d8dba4555c1c2149e8c8c600d7afe04b2abc986f1cec6b535b2b9f577_light.svg)
Die Tangente

besitzt im Punkt

somit die Steigung

.
2. Schritt: Parameter  bestimmen
bestimmen
Um den Parameter

zu bestimmen, sodass

und

sich senkrecht schneiden, wendest du die Bedingung aus der Aufgabenstellung an, und löst die Gleichung nach

auf:
![\(\begin{array}[t]{rll}
k_1\cdot k_2&=& -1 &\quad \scriptsize \mid\; \cdot\dfrac{1}{k_1} \\[5pt]
k_2 &=& -\dfrac{1}{k_1}
\end{array}\)](https://www.schullv.de/resources/formulas/145fcd4c99d60f9528510a33034dce48e58deb5a9fcbfde030aa84812c3699c9_light.svg)
Da

gilt, kannst du für alle

das zugehörige

berechnen. Somit gibt es immer Tangenten, welche sich an der Stelle

senkrecht schneiden.
 Verhältnis der Tangenten und Nullstellen Parameter begründen
Verhältnis der Tangenten und Nullstellen Parameter begründen
Du sollst begründen, warum

doppelt so groß ist wie

, wenn die Nullstelle der Tangente


halb so weit vom Ursprung entfernt ist wie

. Zur Vereinfachung dieses Problems bestimmst du zuerst die Funktionsgleichung der Tangente

und die zugehörige Nullstelle

.
1. Schritt: Funktionsgleichung bestimmen
Alle Tangenten

verlaufen durch den Punkt

und besitzen die Steigung

.
 Lösungsweg A: Allgemeine Tangentengleichung
Lösungsweg A: Allgemeine Tangentengleichung
Alle Tangenten an eine Funktion lassen sich in folgender Form schreiben. Dabei bezeichnet

die Stelle an welcher die Tangente an der Graphen angelegt wird.
Du benötigst die Tangentengleichug an der Stelle

, dort gilt

und

.
![\(\begin{array}[t]{rll}
y&=& f_k‘(0)\cdot (x-0)+f(0)&\\[5pt]
&=& k\cdot x+1
\end{array}\)](https://www.schullv.de/resources/formulas/8cbae8c897ef339c37186f9acbf740f8c9f56562395f3baa8ef1f1a12b89c5f8_light.svg)
Die Tangenten durch

an die Graphen von

haben die Form

.
 Lösungsweg B: Allgemeine Geradengleichung
Lösungsweg B: Allgemeine Geradengleichung
Alle Tangenten sind Geraden und lassen sich somit durch die Form

ausdrücken.
Du benötigst die Steigung

sowie den Ordinatenabschnitt

um die Tangente an den Graphen

durch den Punkt

zu bestimmen.
Die Tangenten durch

an die Graphen von

haben die Form

.
2. Schritt: Nullstelle berechnen
Alle Nullstellen zeichen sich durch den

-Wert

aus. Du setzt die Geradengleichung

und löst sie nach der Nullstelle

auf.
![\(\begin{array}[t]{rll}
0&=& k\cdot x_k+1 &\quad \scriptsize \mid\; -1 \\[5pt]
-1&=& k\cdot x_k &\quad \scriptsize \mid\; \cdot\dfrac{1}{k} \\[5pt]
-\dfrac{1}{k} &=& x_k
\end{array}\)](https://www.schullv.de/resources/formulas/20f026565897bccd6f0ea2f862f8f6909591b9d37827823999d34213d258801d_light.svg)
Die Nullstellen der Tangenten

haben den

-Wert

.
3. Schritt: Aussage begründen
Die Tangenten

und

haben ihre Nullstellen bei

beziehungsweise

.
Der Aufgabenstellung nach, ist zu prüfen wie

und

im Verhältnis stehen wenn

halb so groß ist wie

, also

gilt. Betrachte die Nullstelle

der Tangente

:
Damit ist gezeigt, dass

gilt, wenn

gilt.
b)
 Volumen der Kegel bestimmen
Volumen der Kegel bestimmen
Das Dreieck zwischen den Punkten

,

und

umschließt ein Dreieck. Der Rotationskörper dieses Dreiecks bildet einen Kegel aus. Dessen Volumen du mit

verifizieren sollst.
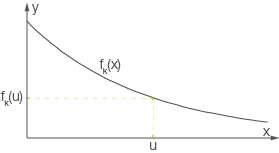 Abb. 1: Skizze des rechtwinkligen Dreiecks
Abb. 1: Skizze des rechtwinkligen Dreiecks
 Lösungsweg A: Rotationsvolumen
Lösungsweg A: Rotationsvolumen
Um das Volumen des Kegels zu berechnen, bestimmst du die Geradengleichung der Hypothenuse des rechtwinkligen Dreiecks, welche die Punkte

und

verbindet und berechnest daraus dann das Rotationsvolumen.
1. Schritt: Geradengleichung bestimmen
Die Gerade verbindet die Punkte

und

. Du benötigst Steigung udn Ordinatenabschnitt.
Die Steigung

bestimmst du mittels eines Steigungsdreiecks:
![\(\begin{array}[t]{rll}
m&=& \dfrac{\Delta y}{\Delta x} &\\[5pt]
&=& \dfrac{f_k(u)-0}{u-0} \\[5pt]
&=& \dfrac{\mathrm e^{k\cdot u}}{u}
\end{array}\)](https://www.schullv.de/resources/formulas/62f514938b5d29d3e5f05828ee6e167f185f574780ecf5352bb4c808dea686f8_light.svg)
Die Steigung der Geraden ist

. Da es sich um eine Ursprungsgerade handelt, gilt für den Ordinatenabschnitt

.
Du erhälst die Geradengleichung:
![\(\begin{array}[t]{rll}
y&=& \dfrac{\mathrm e^{k\cdot u}}{u}\cdot x &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0c25af07baa6fbcae244ab1ffc94bd1cd568371f29af11d33bc2aa7d8f841f4d_light.svg) 2. Schritt: Rotatiosnvolumen bestimmen
2. Schritt: Rotatiosnvolumen bestimmen
Das Rotationsvolumen einer Funktion

ist zwischen den Stellen

und

definiert durch:
Für die Geradengleichung als Funktion und

sowie

als Grenzen ergibt sich das Volumen des Kegels mit:
Der Kegel hat das Volumen

.
 Lösungsweg B: Kegelvolumen
Lösungsweg B: Kegelvolumen
Du kannst den Funktionswert

als Radius der Grundfläche eines liegenden Kegels mit der Höhe

verwenden. Für das Volumen eines Kegels gilt:
Mit dem Radius

und der Höhe

ergibt sich für das Volumen

:
![\(\begin{array}[t]{rll}
V_k(u)&=& \dfrac{1}{3}\cdot\pi\cdot \left(f_k(u)\right)^2\cdot u &\\[5pt]
&=& \dfrac{1}{3}\cdot\pi\cdot\left(\mathrm e^{k\cdot u}\right)^2\cdot u \\[5pt]
&=& \dfrac{\pi}{3}\cdot u\cdot \mathrm e^{2\cdot k\cdot u}
\end{array}\)](https://www.schullv.de/resources/formulas/2d9a581222673d5faeb43f60c48d0e171eacc5b1513b73f5253c73d356f552e6_light.svg)
Der Kegel hat das Volumen

.
 Unabhängigkeit des maximalen Volumens nachweisen
Unabhängigkeit des maximalen Volumens nachweisen
Um zu überprüfen, ob der Grundkreisradius unabhängig vom Parameter

ist, bestimmst du zuerst den Wert für

welcher

maximiert.
Die dafür nötige erste und zweite Ableitung ist in der Aufgabenstellunng gegeben mit:
1. Schritt: Ableitung null setzen
Zur Bestimmung der Extremstellen der Volumenfunktion setzt du deren erste Ableitung

:
An der Stelle

hat die Volumenfunktion einen Extrempunkt.
2. Schritt: Art des Extrempunkts prüfen
Zur Prüfung der Art des Extrempunktes setzt du diesen in die zweite Ableitung ein. Für ein Maximum und Hochpunkt ist die zweite Ableitung negativ.
Da

ist der Term

ebenfalls kleiner als

. An der Stelle

liegt ein Hochpunkt vor. Das Volumen ist an dieser Stelle somit maximal.
3. Schritt: Grundkreisradius berechnen
Mit der Stelle

berechnest du den Grundkreisradius

:
![\(\begin{array}[t]{rll}
r&=& f_k\left(-\dfrac{1}{2\cdot k}\right) &\\[5pt]
&=& \mathrm e^{k\cdot\left(-\dfrac{1}{2\cdot k}\right)} \\[5pt]
&=& \mathrm e^{-\dfrac{1}{2}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/04e4d1bc335bd4a611d7963ca6857e510a911929675ba2105e50bd6d19b48054_light.svg)
Die Kegel mit dem maximalen Volumen haben den Grundkreisradius

, dieser ist unabhängig von

und somit für alle Kegel an allen Funktionen der Schar gleich.
c)
 Stelle, an der Tangenten parallel zueinander sind bestimmen
Stelle, an der Tangenten parallel zueinander sind bestimmen
Du sollst die Stelle bestimmen, an der die Tangenten an

und

parallel zueinander verlaufen, also die gleiche Steigung besitzen. Da die Steigung einer Tangente an der Stelle

der Steigung der Funktion an der Stelle

entspricht, musst du

und

gleichsetzten und nach

auflösen.
![\(\begin{array}[t]{rll}
f_4‘(x)&=&g‘(x) \\[5pt]
4\text{e}^{4x}&=&-16\cdot x\cdot \text{e}^{4x}-4\cdot \text{e}^{4x} &\quad \scriptsize \mid\;+16\cdot x\cdot \text{e}^{4x}+4\cdot \text{e}^{4x} \\[5pt]
4\text{e}^{4x}+16\cdot x\cdot \text{e}^{4x}+4\cdot \text{e}^{4x}&=&0\\[5pt]
8\text{e}^{4x}+16\cdot x\cdot \text{e}^{4x}&=&0 &\quad \scriptsize \mid\;\text{Faktorisieren} \\[5pt]
8\text{e}^{4x}\cdot (1+2x)&=&0
\end{array}\)](https://www.schullv.de/resources/formulas/59d6e1d70da8def429705c8623f697b2956aec9087636b55ce27c0b294ce242c_light.svg)
Nach dem Satz vom Nullprodukt ist die Gleichung genau dann erfüllt, wenn einer der beiden Faktoren Null ist. Die Exponentialfunktion ist für kein

Null. Damit ist die Gleichung nur erfüllt, wenn

gilt.
![\(\begin{array}[t]{rll}
1+2x&=&0 &\quad \scriptsize \mid\;-1 \\[5pt]
2x&=&-1 &\quad \scriptsize \mid\;:2\\[5pt]
x&=&-\dfrac{1}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/8fdb13c77c9bb20a100186499f1f47315f0d3d998d699fdd55b4129bb8e82992_light.svg)
Die beiden Tangenten verlaufen an der Stelle

parallel zueinander.
 Differenz der
Differenz der  Achsen Abschnitte bestimmen
Achsen Abschnitte bestimmen
Die Tangentengleichungen an der Stelle

kannst du mit den folgenden Gleichungen bestimmen:


Die

Achsen Abschnitte sind

und

.
Die Differenz der

Achsen Abschnitte ist:
![\(\begin{array}[t]{rll}
g(-\frac{1}{2})-f_4(-\frac{1}{2})&=& 2\text{e}^{-2}-\text{e}^{-2} \\[5pt]
&=&\text{e}^{-2}\\[5pt]
&\approx& 0,14
\end{array}\)](https://www.schullv.de/resources/formulas/52b5de50a49adf09b0389cfdf0ec94f316a0f848144a6df24078926eb4983077_light.svg)
Die Differenz der

Achsenabschnitte ist

.
 Konzept zu Berechnung des Verhältnises der Flächeninhalte erstellen
Konzept zu Berechnung des Verhältnises der Flächeninhalte erstellen
Um das Verhältnis der Flächeninhalte zu bestimmen musst du die Flächeninhalte zunächst berechnen. Es handelt sich um Flächeninhalte zwischen

und

im Intervall
![\([-0,5;v]\)](https://www.schullv.de/resources/formulas/2f75a2570ef9db20fa64bfbccee823d60f42f7ab1285e9ad87fd0924584900ce_light.svg)
und
![\([v;0]\)](https://www.schullv.de/resources/formulas/5e56cda5d146d1cb0e83ff53749cc77c1304338ec82c98396a7da6ef81a8cb21_light.svg)
. Flächeninhalte zwischen Kurven berechnest du mit dem Integral über den Betrag der Differenz von

und

. Bevor du die Integrale berechnen kannst, musst du

bestimmen.

 bestimmen
bestimmen
Bestimme den Schnittpunkt

der Kurven

und

.
![\(\begin{array}[t]{rll}
f_4(v)&=&g(v)\\[5pt]
\text{e}^{4v}&=&-4x\text{e}^{4v} &\quad \scriptsize \mid\;:\text{e}^{4v}\\[5pt]
1&=&-4v &\quad \scriptsize \mid\;:(-4)\\[5pt]
x&=& -\frac{1}{4}
\end{array}\)](https://www.schullv.de/resources/formulas/58be0d1ca458cf84a47eda433934a9436f5d8183d3a9b39284d53449deab58a2_light.svg)
Der Schnittpunkt und damit die unbekannte Integrationsgrenze ist

 Flächeninhalte zwischen den Kurven bestimmen
Flächeninhalte zwischen den Kurven bestimmen
Berechne zuerst die Fläche zwischen

und

im Intervall
![\([-0,5;-0,25]\)](https://www.schullv.de/resources/formulas/5af2d89d6ce65095de31ef1003c950fa03136503c15fdb9e7d6214268addfe03_light.svg)
und nenne diese Fläche

. In diesem Intervall verläuft

oberhalb von

. Berechne den Wert des Integrals mit deinem Taschenrechner.
![\(\begin{array}[t]{rll}
A_1&=&\int_{-0,5}^{-0,25} |f_4(x)-g(x)| dx \\[5pt]
&=&\int_{-0,5}^{-0,25}g(x)- f_4(x) dx \\[5pt]
&=& 0,024
\end{array}\)](https://www.schullv.de/resources/formulas/15e3d590da62729d1bf4c9126477e37132abecfc3a34c32c0fa23498d6f68886_light.svg)
Berechne als Nächstes die Fläche zwischen

und

im Intervall
![\([-0,25;0]\)](https://www.schullv.de/resources/formulas/a4f719978532fdc8ce08154186b9a3fe634f47e82aca7565656aa36b0000b66d_light.svg)
und nenne diese Fläche

. In diesem Intervall verläuft

oberhalb von

. Berechne den Wert des Integrals mit deinem Taschenrechner.
![\(\begin{array}[t]{rll}
A_2&=&\int_{-0,25}^{0} |f_4(x)-g(x)| dx \\[5pt]
&=&\int_{-0,5}^{-0,25} f_4(x)-g(x) dx \\[5pt]
&=& 0,091
\end{array}\)](https://www.schullv.de/resources/formulas/a3c471cd3796354a7b5bf72425a6ccfe2b9d1a0ccf3682c0aee89afdf1cd4f85_light.svg)
Das Verhältnis der Flächen ist:

.
 Häufigkeit der Steigungswerte analysieren
Häufigkeit der Steigungswerte analysieren
Du sollst untersuchen, welche Steigungswerte der Graph von

genau einmal bzw. genau zweimal annimmt. Untersuche dazu die Funktion

.
Betrachte als erstes den Wert

. Dieser Steigungswert wird von

an allen Stellen angenommen, an denen die Ableitungsfunktion Null ist. Da

für jedes

größer als Null ist, halt

die einzige Nullstelle

. Der Steigungswert

wird also einmal angenommen.
Betrachte als Nächstes die Werte

. Für diese Werte ist

streng monoton fallend. Außerdem ist

. Jede negative reelle Zahl wird genau einmal als Steigungswert angenommen.
Betrachte als Letztes die Werte

. Für diese Werte ist

positiv und hat ein Maximum bei

. Da

für

, nimmt

alle Steigungswerte zwischen

und

genau zwiemal und den Maximalwert

genau einmal an.
d)
 Ungleichung begründen
Ungleichung begründen
Du sollst mit Hilfe der beiden Integrale

und

die Abschätzung

für alle

nachweisen.
Untersuchte dazu die Integranden

und

.
Für

haben beide den gleichen Funktionswert

. Allerdings ist die Steigung der

-Funktion immer größer als die der Gerade, deren Steigung konstant

ist.
Somit gilt für alle

-Werte größer

, dass

größer als

ist.
Bestimmst du den Wert derIntegrale, erhältst du:
![\(\begin{array}[t]{rll}
\int\limits_0^x\mathrm e^t\;\mathrm d t& \gt & \int\limits_0^x (1+t)\;\mathrm d t &\\[5pt]
\mathrm e^x-1& \gt & x+\dfrac{x^2}{2} &\quad\scriptsize\mid \; +1 \\[5pt]
\mathrm e^x & \gt & 1+x+\dfrac{x^2}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/bba8a6e49c7acb1a3b3c60da74a44328a3a001b620ae289158acb1fea49e1505_light.svg)
Damit ist die Ungleichung nachgewiesen.
Bildnachweise [nach oben]
© 2016 - SchulLV.
 für
für  und
und  .
Entscheide, welche der Funktionen zu welchem Graphen gehört.
Berechne die
.
Entscheide, welche der Funktionen zu welchem Graphen gehört.
Berechne die  -Koordinate des Punktes, in dem die Tangente an den Graphen von
-Koordinate des Punktes, in dem die Tangente an den Graphen von  die Steigung
die Steigung  hat.
Für jeden Wert von
hat.
Für jeden Wert von  bezeichnet
bezeichnet  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  .
Zeige, dass es zu jedem Parameter
.
Zeige, dass es zu jedem Parameter  einen davon verschiedenen Parameter
einen davon verschiedenen Parameter  gibt, sodass sich die Tangenten
gibt, sodass sich die Tangenten  und
und  senkrecht schneiden. Ohne Nachweis kannst du verwenden: Wenn für die Steigungen
senkrecht schneiden. Ohne Nachweis kannst du verwenden: Wenn für die Steigungen  und
und  zweier Geraden die Beziehung gilt:
zweier Geraden die Beziehung gilt:  , dann stehen die zugehörigen Geraden senkrecht aufeinander.
Jede Tangente
, dann stehen die zugehörigen Geraden senkrecht aufeinander.
Jede Tangente  hat eine Nullstelle. Die Nullstelle der Tangente
hat eine Nullstelle. Die Nullstelle der Tangente  wird mit
wird mit  bezeichnet und die Nullstelle der Tangente
bezeichnet und die Nullstelle der Tangente  wird mit
wird mit  bezeichnet.
Begründe, dass der Wert von
bezeichnet.
Begründe, dass der Wert von  doppelt so groß ist wie der Wert von
doppelt so groß ist wie der Wert von  , wenn
, wenn  halb so groß ist wie
halb so groß ist wie  .
.
 werden nun mit den folgenden Bedingungen betrachtet:
werden nun mit den folgenden Bedingungen betrachtet:  und
und  .
Für jeden Wert von
.
Für jeden Wert von  wird dem Graphen von
wird dem Graphen von  ein rechtwinkliges Dreieck einbeschrieben. Für eine Stelle
ein rechtwinkliges Dreieck einbeschrieben. Für eine Stelle  sind
sind  ,
, und
und  die Eckpunkte. Bei Rotation dieser Dreiecke um die
die Eckpunkte. Bei Rotation dieser Dreiecke um die  -Achse entstehen Kegel.
Zeige, dass für die Volumen
-Achse entstehen Kegel.
Zeige, dass für die Volumen  der Kegel gilt:
der Kegel gilt:  .
Untersuche, ob die Kegel mit dem maximalen Volumen für jeden Wert des Parameters
.
Untersuche, ob die Kegel mit dem maximalen Volumen für jeden Wert des Parameters  denselben Grundkreisradius haben. Ohne Nachweis kannst du verwenden:
denselben Grundkreisradius haben. Ohne Nachweis kannst du verwenden:
 und
und  .
.
 werden nun die Funktion
werden nun die Funktion  sowie die Funktion
sowie die Funktion  mit der Gleichung
mit der Gleichung  betrachtet.
betrachtet.
 bezeichnet die Tangente an den Graphen von
bezeichnet die Tangente an den Graphen von  an der Stelle
an der Stelle  und
und  bezeichnet die Tangenten an den Graphen von
bezeichnet die Tangenten an den Graphen von  an dieser Stelle
an dieser Stelle  . Es gibt eine Stelle, an der die Tangenten
. Es gibt eine Stelle, an der die Tangenten  und
und  parallel zueinander verlaufen.
Bestimme die Differenz der y-Achsenabschnitte dieser parallelen Tangenten.
Die Graphen von
parallel zueinander verlaufen.
Bestimme die Differenz der y-Achsenabschnitte dieser parallelen Tangenten.
Die Graphen von  und
und  schneiden sich an einer Stelle
schneiden sich an einer Stelle  und begrenzen zwei Flächen: Eine liegt rechts von
und begrenzen zwei Flächen: Eine liegt rechts von  und wird rechts von der
und wird rechts von der  -Achse begrenzt und eine liegt links von
-Achse begrenzt und eine liegt links von  und wird von der Geraden zu
und wird von der Geraden zu  begrenzt.
Bestimme das Verhältnis der Inhalte beider Flächen. Die Funktion
begrenzt.
Bestimme das Verhältnis der Inhalte beider Flächen. Die Funktion  wird nun für alle
wird nun für alle  betrachtet.
Untersuche, welche Steigungswerte der Graph von
betrachtet.
Untersuche, welche Steigungswerte der Graph von  genau einmal und welche Steigungswerte er genau zweimal annimmt.
genau einmal und welche Steigungswerte er genau zweimal annimmt.
 und
und  , dass für
, dass für  gilt:
gilt:
 .
.
 ,
,  und
und  umschließt ein Dreieck. Der Rotationskörper dieses Dreiecks bildet einen Kegel aus. Dessen Volumen du mit
umschließt ein Dreieck. Der Rotationskörper dieses Dreiecks bildet einen Kegel aus. Dessen Volumen du mit  verifizieren sollst.
verifizieren sollst.
 Abb. 1: Skizze des rechtwinkligen Dreiecks
Abb. 1: Skizze des rechtwinkligen Dreiecks