Aufgabe 2B

Im Zusammenhang mit der Veröffentlichung eines neuen Spiels im Internet werden Simulationen durchgeführt, bei denen die vom Anbieter bereitzustellenden Rechnerkapazitäten untersucht werden. Dabei wird auch berücksichtigt, wieviel Zeit ein Benutzer bis zu einer bestimmten Reaktion benötigt.
Diese Zeit wird Reaktionszeit genannt und in Sekunden ( $\text{s}$ ) gemessen.

Für diese bestimmte Reaktion wird eine erste Simulation durchgeführt. Dazu wird die Reaktionszeit als normalverteilte Zufallsgröße $X$ angenommen. Eine Schätzung liefert den Erwartungswert $\mu_{X}=3,2$ und die Standardabweichung $\sigma_{X}=0,6$
Bestimme

den Anteil der Reaktionszeiten, die länger als $4\,\text{s}$ dauern,

den Anteil der Reaktionszeiten, deren Abweichung vom Erwartungswert kleiner als $1 \text{s}$ ist,

die untere Grenze eines Zeitintervalls, in dem $80\,\%$ der Zeiten liegen und dessen obere Grenze $4\,\text{s}$ beträgt.

(9P)

Nach der Veröffentlichung dieses Spiels werden Reaktionszeiten gemessen. Gegeben ist hier ein Auszug von $10$ Messdaten:

Nr.	1	2	3	4	5	6	7	8	9	10
Zeit in s	3,18	3,02	2,95	3,18	4,04	2,80	2,64	2,41	2,64	3,18

Berechne das arithmetische Mittel und die Standardabweichung für diese Daten.

Anhand aller gemessenen Daten soll ein zweites Modell für weitere Simulationen entwickelt werden. Dazu soll die Reaktionszeit als normalverteilte Zufallsgröße $Y$ mit dem Erwartungswert $\mu_{Y}=3,0$ beschrieben werden. Außerdem sollen mindestens $80\,\%$ der Reaktionszeiten unterhalb von $3,5\,\text{s}$ liegen.
Bestimme die größte Standardabweichung auf $0,01\,\text{s}$ genau, für die dies gilt.

(8P)

Unabhängig vom Sachzusammenhang werden im Folgenden normalverteilte Zufallsgrößen $Z_\sigma$ mit dem Erwartungswert $\mu=3$ betrachtet. Die Funktion $W$ gibt für Werte der Standardabweichung $\sigma$ mit $\sigma > 0$ die Wahrscheinlichkeit $P\left(Z_{\sigma} \leq 2\right)$ an.

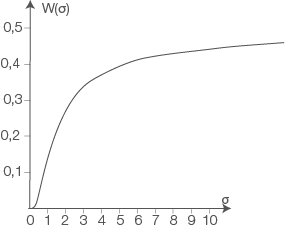
Die Abbildung 1 zeigt den Graphen von $W$ .
Erläutere den Wert $W(1)$ mithilfe einer Skizze des Graphen der zugehörigen Dichtefunktion der Normalverteilung.
Erläutere unter Bezug auf die Graphen der Dichtefunktionen der zugehörigen Normalverteilungen, dass der Graph von $W$ für $\sigma > 1$ monoton steigt, aber unterhalb der Geraden zu $y=0,5$ liegt.

Graph mit der Funktion W(ω) in Bezug auf ω, zeigt einen asymptotischen Verlauf.

Abb. 1: Graph von $W$

(7P)

Bildnachweise [nach oben]

[1]

$\blacktriangleright$ Anteil der Reaktionszeiten über $\boldsymbol{4}\;\text{s}$ berechnen

Um den Anteil der Reaktionszeiten über $4\;\text{s}$ beim Onlinespiel zu bestimmen, betrachtest du die Verteilungsfunktion $\Phi$ .

Die Funktion $\Phi$ gibt an, welcher Anteil der Ereignisse unter einer oberen Grenze $a$ liegt. Dabei ist diese Grenze $a$ lediglich ein Bestandteil des Argumentes der Funktion. Das komplette Argument enthält desweiteren den Erwartungswert $\mu_x$ und die Standardabweichung $\sigma_x$ in der Form $\dfrac{a-\mu_x}{\sigma_x}$ .

Der Anteil der Reaktionszeiten unter $4\;\text{s}$ ist somit gegeben durch $\Phi\left(\dfrac{4-3,2}{0,6}\right)=\Phi\left(\dfrac{4}{3}\right)$ .

Da es sich bei längeren Zeiten um das Gegenereignis handelt berechnest du $P(X\gt 4)$ mit:

$P(X\gt 4)\approx 0,09$

Vollständige Lösung anzeigen

Es sind $0,09=9\%$ der Reaktionszeiten länger als vier Sekunden.

$\blacktriangleright$ Wahrscheinlichkeit für kleine Abweichung vom Erwartungswert

Du sollst berechnen, mit welcher Wahrscheinlichkeit ein Messwert eine Abweichung von weniger als $1\;\text{s}$ vom Erwartungswert $\mu_x=3,2$ hat. Du berechnest somit die Wahrscheinlichkeit, dass ein Messwert innerhalb des Intervalls $\left(2,2\; ; \;4,2\right)$ liegt.

Das Intervall $\left(2,2\; ; \;4,2\right)$ entspricht einem $1,6-\sigma$ -Intervall um den Erwartungswert. In einem $1,6-\sigma$ -Intervall liegen $90\%$ aller Ereignisse.

Die Wahrscheinlichkeit beträgt also: $P(2,2\leq X\leq 4,2)=0,9$ .

$\blacktriangleright$ Intervallgrenze berechnen

Du sollst die untere Intervallgrenze $a$ bestimmen, sodass $P(a\leq X\leq 4)=0,8$ gilt. Betrachte dazu die $\Phi$ -Funktion. Du weißt, diese gibt an, welcher Anteil unterhalb einer bestimmten Grenze liegt. Für die Wahrscheinlichkeit innerhalb eines Intervalls gilt somit:

$\begin{array}[t]{rll} P(a\leq X\leq b)&=& \Phi\left( \dfrac{b-\mu_x}{\sigma_x} \right) &\\[5pt] & & -\Phi\left( \dfrac{a-\mu_x}{\sigma_x} \right) \end{array}$

In diesem Fall untersuchst du die Gleichung:

$c\approx -1,23$

Vollständige Lösung anzeigen

Es gilt $c\approx -1,23$ . Um die Intervallgrenze $a$ zu bestimmen, ist eine weitere Gleichung zu lösen.

$a\approx 2,462$

Vollständige Lösung anzeigen

Die untere Intervallgrenze liegt bei $2,462$ , somit liegen im Intervall $(2,462\; ; \;4)$ $80\%$ aller Reaktionszeiten.

$\blacktriangleright$ Arithmetisches Mittel berechnen

Es wurde eine Messreihe mit $n=10$ Messungen durchgeführt und die Reaktionszeiten $x_i$ gemessen. Aus den Daten sollst du das arithmetische Mittel $\overline{x}$ berechnen. Für das arithmetische Mittel gilt:

$\overline{x}=\dfrac{1}{n}\cdot\sum\limits_{i=1}^{n} x_i$

Für das Mittel berechnest du die Summe aller Zeiten und teilst sie durch die Anzahl der Summanden.

$\overline{x}=3,004$

Vollständige Lösung anzeigen

Es gilt für das arithmetische Mittel $\overline{x}=3,004$ .

$\blacktriangleright$ Standardabweichung berechnen

Die Standardabweichuung einer Messreihe berechnet sich mit:

$\sigma=\sqrt{\dfrac{1}{n-1}\cdot\sum\limits_{i=1}^n (x_i-\overline{x})^2}$

Für diese Messreihe aus $10$ Messpunkten ergibt sich:

$\begin{array}[t]{rll} \sigma&=& \sqrt{\dfrac{1}{10-1}\cdot\sum\limits_{i=1}^{10} (x_i-\overline{x})^2} &\\[5pt] &\approx& \sqrt{\dfrac{1}{9}\cdot 1,83} \\[5pt] &\approx& \sqrt{0,203} \\[5pt] &\approx& 0,451 \end{array}$

Die Standardabweichung der Messwerte beträgt $0,451$ .

$\blacktriangleright$ Größte Standardabweichung bestimmen

Die gemessenen Werte sollen durch ein Modell anhand einer Normalverteilung beschrieben werden. Es wird angenommen, dass der Erwartungswert bei $\mu_Y=3,0$ liegt. Desweiteren sollen mindestens $80\%$ aller Reaktionszeiten kleiner als $3,5\;\text{s}$ sein.

Aus diesen Daten soll die Standardabweichung bestimmt werden. Zur Lösung betrachtest du die Verteilungsfunktion $\Phi$ .

$c\approx 0,85$

Vollständige Lösung anzeigen

Das Argument der $\Phi$ -Funktion muss $0,85$ sein. Daraus berechnest du die Standardabweichung.

$\begin{array}[t]{rll} 0,85&=& \dfrac{1}{2\cdot\sigma_Y} &\quad \scriptsize \mid\; \cdot\sigma_Y \\[5pt] 0,85\cdot \sigma_Y&=& \dfrac{1}{2} &\quad \scriptsize \mid\; : 0,85 \\[5pt] \sigma_Y&=& \dfrac{1}{2\cdot 0,85} \\[5pt] &\approx & 0,59 \end{array}$

Die größtmögliche Standardabweichung ist $\sigma_Y=0,59$ .

$\blacktriangleright$ Wert $\boldsymbol{W(1)}$ erläutern

Die Funktion $W$ beschreibt die Wahrscheinlichkeit, dass eine normalverteilte Zufallsvariable $Z_\sigma$ mit Erwartungswert $\mu=3$ einen Wert kleiner $2$ annimmt.

Die Funktionsvorschrift ist somit: $W(\sigma)=P(Z_\sigma\leq 2)=\Phi\left(\dfrac{2-3}{\sigma}\right)$ .

Du sollst nun den Wert $W(1)$ und somit die Wahrscheinlichkeit $P(Z_1\leq 2)$ bestimmen.

Die Standardabweichung beträgt $\sigma=1$ . Das $1-\sigma$ -Intervall um den Erwartungswert ist somit $(2\, ; \, 4)$ .

In das $1-\sigma$ -Intervall um den Erwartungswert $\mu$ fallen $68,27\%$ aller Ereignisse.

Außerhalb dieses Intervalls liegen die restlichen $31,73\%$ . Diese teilen sich jedoch auf sehr große und sehr kleine Werte auf.

Unterhalb des Intervalls liegt somit genau die Hälfte der Restwahrscheinlichkeit, somit genau $15,87\%$ .

An der Stelle $1$ hat die Funktion $W$ damit den Wert $W(1)=P(Z_1\leq 2)=0,1587$ .

Grafik einer Normalverteilung mit beschrifteten Bereichen und Prozentsätzen.

Abb. 1: Normalverteilung mit $1-\sigma$ -Intervall

$\blacktriangleright$ Monotonie von $\boldsymbol{W}$ erläutern

Du sollst erläutern, warum der Graph der Funktion $W$ , für $\sigma\gt 1$ monoton wächst und immer kleiner als $0,5$ ist.

Dazu überlegst du, wie sich die Verteilungsdichte mit wachsendem $\sigma$ ändert.

Steigt die Standardabweichung bei gleichbleibendem Erwartungswert an, so breitet sich der Graph der Verteilungsdichtefunktion auf. Gleichzeitig sinkt aber das Maximum beim Erwartungswert ab, da die Fläche unter der Kurve weiterhin auf $1$ normiert ist.

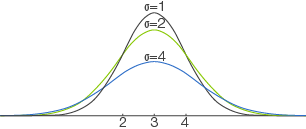Grafik mit Kurven für verschiedene Werte von σ (1, 2, 4) in einem Koordinatensystem.

Abb. 2: Verbreiterung der Glockenkurve

Dadurch, dass sich die Kurve weiter breitet, liegt mehr Fläche unter der Kurve innerhalb des Intervalls $(-\infty\, ; \, 2)$ und somit steigt die Funktion $W$ stetig an.

Das die Funktion $W$ ebenfalls nie den Wert $0,5$ erreicht, folgt aus der Symmetrie des Graphens der Dichtefunktion. $50\%$ aller Ereignisse liegen rechts der Erwartungswertes, die restlichen $50\%$ liegen links davon. Aber von diesen $50\%$ liegt immer auch ein Teil im Bereich zwischen $2$ und $3$ und fließt nicht in den Wert von $W$ ein.

Dadurch ist $W(x)$ immer kleiner als $0,5$ .

Bildnachweise [nach oben]

[1]

[2]