Pflichtteil

Aufgabe P1

Gegeben sind die in $ℝ$ definierten Funktionen $f$ , $g$ und $h$ durch

$f(x)=x^2-x+1$ ,

$g(x)=x^3-x+1$ und

$h(x)=x^4+x^2+1$ .

a) Die Abbildung zeigt den Graphen einer der drei Funktionen.

Gib an, um welche Funktion es sich handelt.

Begründe, dass der Graph die anderen beiden Funktionen nicht darstellt.

(3P)

Koordinatensystem mit Achsen und Gitternetzlinien.

b) Die erste Ableitungsfunktion von $h$ ist $h‘$ . Bestimme den Wert von $\mathop{\displaystyle\int}\limits_{0}^{1}h‘(x)\mathrm\,{dx}$ .

(2P)

Aufgabe P2

Für jeden Wert von $a$ $(a\gt 0)$ ist eine Funktion $f_a$ gegeben durch $f_a(x)=x\cdot \mathrm{e}^{-a\cdot x}$ $(x \in ℝ)$ .

In der nebenstehenden Abbildung ist beispielhaft für $a=2$ der Graph von $f_2$ sowie von $\(f_2$ dargestellt.

Es ist $f_2‘(0)=1$ .

Koordinatensystem mit Achsenbeschriftungen für x und y, dargestellt in einem einfachen Raster.

a) Begründe, dass $y=x$ die Gleichung der Tangente an den Graphen von $f_2$ an der Stelle $x=0$ ist.

(2P)

b) Zeige, dass gilt: $f_a‘(x)=(1-a\cdot x)\cdot \mathrm{e}^{-a\cdot x}$ $(x \in ℝ , a\gt 0)$ .

(2P)

c) Begründe, dass die Extremstellen der Graphen von $f_a$ vom Parameter $a$ abhängig sind, die Nullstellen aber nicht.

(2P)

Aufgabe P3

Bei der Wintersportart Biathlon wird bei jeder Schießeinlage auf fünf Scheiben geschossen. Ein Biathlet tritt bei einem Einzelrennen zu einer Schießeinlage an, bei der er auf jede Scheibe einen Schuss abgibt. Diese Schießeinlage wird modellhaft durch eine Bernoullikette mit der Länge $5$ und der Trefferwahrscheinlichkeit $p$ beschrieben.

a) Gib für die folgenden Ereignisse jeweils einen Term an, der die Wahrscheinlichkeit des Ereignisses in Abhängigkeit von $p$ beschreibt.

Der Biathlet trifft bei genau vier Schüssen.

Der Biathlet trifft nur bei den ersten beiden Schüssen.

(3P)

b) Erläutere anhand eines Beispiels, dass die modellhafte Beschreibung der Schießeinlage durch eine Bernoullikette unter Umständen der Realität nicht gerecht wird.

(2P)

Aufgabe P4

Die Gerade $g$ verläuft durch die Punkte $A\,(0\mid 1\mid 2)$ und $B\,(2\mid 5\mid 6)$ .

a) Zeige, dass die Punkte $A$ und $B$ den Abstand $6$ haben.
Die Punkte $C$ und $D$ liegen auf $g$ und haben von $A$ jeweils den Abstand $12$ .

Bestimme die Koordinaten von $C$ und $D$ .

(3P)

b) Die Punkte $A$ , $B$ und $E\,(1\mid 2\mid 5)$ sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunktes gibt es mehrere Möglichkeiten.

Gib für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunktes an.

(2P)

Aufgabe P5

Zu einem bestimmten Zeitpunkt haben die drei Anbieter $A1$ , $A2$ und $A3$ jeweils 10.000 Kunden. Die für das nächste Jahr zu erwartende Kundenwanderung zwischen diesen Anbietern wird durch die nebenstehende Übergangstabelle beschrieben.

von \ nach	$\boldsymbol{A1}$	$\boldsymbol{A2}$	$\boldsymbol{A3}$
$\boldsymbol{A1}$	$0,90$	$0,02$	$0,02$
$\boldsymbol{A2}$	$0,04$	$0,90$	$0,03$
$\boldsymbol{A3}$	$0,06$	$0,08$	$0,95$

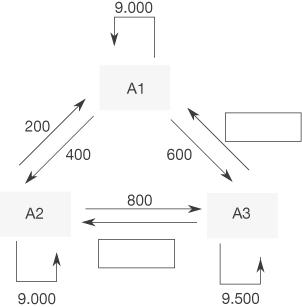
a) Vervollständige den nebenstehenden Übergangsgraphen zur Kundenwanderung innerhalb des nächsten Jahres.
Gib die Gesamtzahl der Kunden an, die innerhalb des nächsten Jahres den Anbieter wechseln.

Diagramm mit drei Knoten A1, A2 und A3, verbunden durch Pfeile und Zahlen.

(2P)

b) Ausgehend von der Ausgangsverteilung von je $10.000$ Kunden wird eine Fusion der Anbieter $A1$ und $A2$ zu einem Anbieter $A1\&A2$ geplant. Im Kundengeschäft behalten beide ihr bekanntes Profil bei, sodass angenommen werden kann, dass die Kundenwanderung im nächsten Jahr weiterhin wie in der obigen Übergangstabelle dargestellt abläuft.

Vervollständige den untenstehenden Übergangsgraphen zur Kundenwanderung innerhalb des nächsten Jahres unter Berücksichtigung der Fusion.

Diagramm mit verschiedenen Elementen und Verbindungen, beschriftet mit A1&A2 und A3.

Vervollständige die nebenstehende Übergangstabelle zur Kundenwanderung innerhalb des nächsten Jahres unter Berücksichtigung der Fusion.

von/nach	$A1\&A2$	$A3$
$A1\&A2$
$A3$		$0,95$

(3P)

Aufgabe P1

a) $\blacktriangleright$ Graph bestimmen

Du hast eine Abbildung eines Graphen und drei Funktionsgleichungen gegeben. Du sollst bestimmen, um welche Funktion es sich handelt.

Der abgebildete Graph ist punktsymmetrisch . Die Funktion $g$ hat nur ungerade Exponenten und ist somit ebenfalls punktsymmetrisch. Bei dem abgebildeten Graphen handelt es sich daher um die Funktion $g$ .

Die Funktion $f$ ist eine Parabel und hat nur einen Extrempunkt. Die Funktion $h$ hat nur gerade Exponenten und ist somit achsensymmetrisch.

b) $\blacktriangleright$ Integral bestimmen

Du sollst folgendes Integral bestimmen:

$\begin{array}[t]{rll} A&=& \displaystyle\int_{0}^{1}\;h‘(x)\mathrm dx \end{array}$

Die Funktion $h‘$ ist die erste Ableitungsfunktion der Funktion $h$ . Somit ist die Funktion $h$ die Stammfunktion von $h‘$ .

$\begin{array}[t]{rll} A&=& \displaystyle\int_{0}^{1}\;h‘(x)\mathrm dx\\[5pt] &=&[h(x)]_0^1\mathrm dx\\[5pt] &=&[x^4+x^2+1]_0^1\\[5pt] &=&1^4+1^2+1-(0^4+0^2+1)\\[5pt] &=&1+1+1-0-0-1\\[5pt] &=&2 \end{array}$

Aufgabe P2

a) $\blacktriangleright$ Gleichung der Tangente begründen

Eine Tangente ist eine Gerade mit der allgemeinen Gleichung $y=mx+b$ . Dabei ist $m$ die Steigung und $b$ der $y$ -Achsenabschnitt.

Die Tangente soll an der Stelle $x=0$ angelegt werden. Du weißt, dass der Graph von $f_2$ durch den Ursprung geht. Der $y$ -Achsenabschnitt ist demnach gleich Null.

Aus der Aufgabe weißt du, dass gilt: $f_2‘(0)=1$

Die Steigung $m$ an der Stelle $x=0$ ist also gleich $1$ .

Die Gleichung der Tangente von $f_2$ an der Stelle $x=0$ ist $y=x$ .

b) $\blacktriangleright$ Gleichung der 1. Ableitung zeigen

Leite $f_a(x)=x\cdot \mathrm e^{-a\cdot x}$ mit Hilfe der Produktregel und der Kettenregel ab:

$\begin{array}[t]{rll} f_a‘(x)=& \mathrm e^{-a\cdot x}+x\cdot (-a) \cdot \mathrm e^{-a\cdot x}& \scriptsize \mid\; \text{Produkt- und Kettenregel angewandt} \\[5pt] =&\left(1-a\cdot x\right) \cdot \mathrm e^{-a\cdot x} \end{array}$

Damit lautet die 1. Ableitung $f_a‘(x)=\left(1-a\cdot x\right) \cdot \mathrm e^{-a\cdot x}$ $(x\in \mathbb{R}, a\gt 0)$ .

c) $\blacktriangleright$ Form der Extrem- und Nullstellen begründen

Den Funktionsterm von $f_a$ kannst du der Aufgabenstellung entnehmen, den der 1. Ableitung der vorigen Teilaufgabe. Mit der hinreichenden Bedingung für eine Extremstelle folgt, dass eine potentielle Extremstelle eine Nullstelle der 1. Ableitung $f_a‘$ ist. Setze dazu den Funktionsterm von $f_a‘$ gleich Null:

$\begin{array}[t]{rll} f_a‘(x)\stackrel{!}{=}&0\\[5pt] \left(1-a\cdot x\right) \cdot \mathrm e^{-a\cdot x}=&0 \end{array}$

Da $\mathrm e^{-a\cdot x}\gt 0$ , erhältst du mit dem Satz vom Nullprodukt :

$\begin{array}[t]{rll} \left(1-a\cdot x\right)=&0 & \scriptsize \mid\; -1\\[5pt] -a\cdot x=-1& \scriptsize \mid\; :(-a)\\[5pt] x=&\frac{1}{a} \end{array}$

Somit sind die potentiellen Extremstellen des Graphen von $f_a$ vom Parameter $a$ abhängig.

Um eine Nullstelle des Graphen von $f_a$ zu ermitteln, setzt du den Funktionsterm von $f_a$ gleich Null:

$\begin{array}[t]{rll} f_a(x)\stackrel{!}{=}&0 \\[5pt] x\cdot \mathrm e^{-a\cdot x}=&0 \end{array}$

Da $\mathrm e^{-a\cdot x}\gt 0$ , erhältst du mit dem Satz vom Nullprodukt :

$x=0$

Somit ist $x=0$ die einzige Nullstelle aller Funktionsgraphen der Schar $f_a$ und unabhängig von $a$ .

Aufgabe P3

a) $\blacktriangleright$ Term für die Wahrscheinlichkeit der Ereignisse angeben

Definiere die Zufallsvariable $X$ , die die Anzahl der Treffer bei einer Schießeinlage angibt. Nach der Aufgabenstellung ist $X$ binomialverteilt mit Wahrscheinlichkeit $p$ und $n=5$ (Anzahl der Versuchen). Allgemein gilt für eine binomialverteilte Zufallsvariable $X$ mit Parametern $p$ und $n$ :

$P(X=k)=\binom{n}{k} \cdot p^k \cdot (1-p)^{n-k}$ .

(1) Die Wahrscheinlichkeit, dass der Biathlet bei genau vier Schüssen trifft, ergibt sich mit $k=4$ :

$\begin{array}[t]{rll} P(X=4)=&\binom{5}{4} \cdot p^4 \cdot (1-p)^{5-4} \\[5pt] =&5\cdot p^4 \cdot (1-p) \end{array}$

Der Biathlet trifft mit Wahrscheinlichkeit $5\cdot p^4 \cdot (1-p)$ bei genau vier Schüssen.

(2) Die Wahrscheinlichkeit, dass der Biathlet nur bei den ersten zwei Schüssen trifft, lässt sich folgendermaßen bestimmen:

Mit der Wahrscheinlichkeit $P(X=2)$ trifft der Biathlet bei genau zwei von den $5$ Versuchen. Es gibt $\binom{5}{2}$ Möglichkeiten, wie diese zwei Treffer verteilt sein können, wobei jede Möglichkeit gleich wahrscheinlich ist. Gesucht ist eine Möglichkeit davon, nämlich dass er bei den ersten beiden Schüssen trifft. Die Wahrscheinlichkeit dafür ergibt sich wie folgt:

$\begin{array}[t]{rll} \dfrac{P(X=2)}{\binom{5}{2}}=&\dfrac{\binom{5}{2} \cdot p^2 \cdot (1-p)^{5-2}}{\binom{5}{2} } \\[5pt] =& p^2 \cdot (1-p)^3 \end{array}$

Der Biathlet trifft nur bei den ersten beiden Schüssen mit der Wahrscheinlichkeit $p^2 \cdot (1-p)^3$ .

b) $\blacktriangleright$ Grenzen der modellhaften Beschreibung erläutern

Bei dieser Teilaufgabe sollst du ein Beispiel nennen, warum die Bernoullikette eventuell nicht der Realität entspricht.

Bei der Bernoullikette wird von einer gleichbleibenden Trefferwahrscheinlichkeit ausgegangen. Dabei wird jedoch nicht die Nervosität des Schützen oder mögliche Veränderungen des Wetters beachtet.

Ein Beispiel wäre, wenn der Biathlet nach den ersten Fehlschüssen zu nervös ist, um sich auf den nächsten Schuss genauso gut konzentrieren. Eine andere Möglichkeit wäre, wenn plötzlich ein Windstoß kommt, der die Kugel abfälscht.

Aufgabe P4

a) (1) $\blacktriangleright$ Abstand $\boldsymbol{d}$ berechnen

Du hast die Punkte $A(0\mid1\mid2)$ und $B(2\mid5\mid6)$ gegeben und sollst zeigen, dass der Abstand zwischen diesen Punkten $6$ LE beträgt.

Den Abstand $d$ zwischen zwei Punkten $P(p_1\mid p_2\mid p_3)$ und $Q(q_1\mid q_2\mid q_3)$ wird mit folgender Formel berechnet:

$\begin{array}[t]{rll} d&=&\sqrt{(p_1-q_1)^2+(p_2-q_2)^2+(p_3-q_3)^2} \end{array}$

Setze nun die Koordinaten der Punkte $A$ und $B$ in diese Formel ein.

$\begin{array}[t]{rll} d&=&\sqrt{(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2} \\[5pt] &=&\sqrt{(0-2)^2+(1-5)^2+(2-6)^2}\\[5pt] &=&\sqrt{(-2)^2+(-4)^2+(-4)^2}\\[5pt] &=&\sqrt{4+16+16}\\[5pt] &=&\sqrt{36}\\[5pt] &=&6 \end{array}$

Die Punkte $A$ und $B$ haben den Abstand von $6$ LE.

a) (2) $\blacktriangleright$ Koordinaten von $\boldsymbol{C}$ und $\boldsymbol{D}$ bestimmen

Du weißt, dass der Abstand zwischen $A$ und $B$ $6$ LE beträgt und beide Punkte auf der Geraden $g$ liegen. Gesucht sind die Koordinaten von $C$ und $D$ , die beide auf der Geraden $g$ liegen und $12$ LE Abstand zu $A$ haben. Diese erhältst du, indem du zweimal den Verbindungsvektor $\overrightarrow{AB}$ zu $\overrightarrow{OA}$ addierst oder davon subtrahierst. Dies erkennst du gut an folgender Skizze:

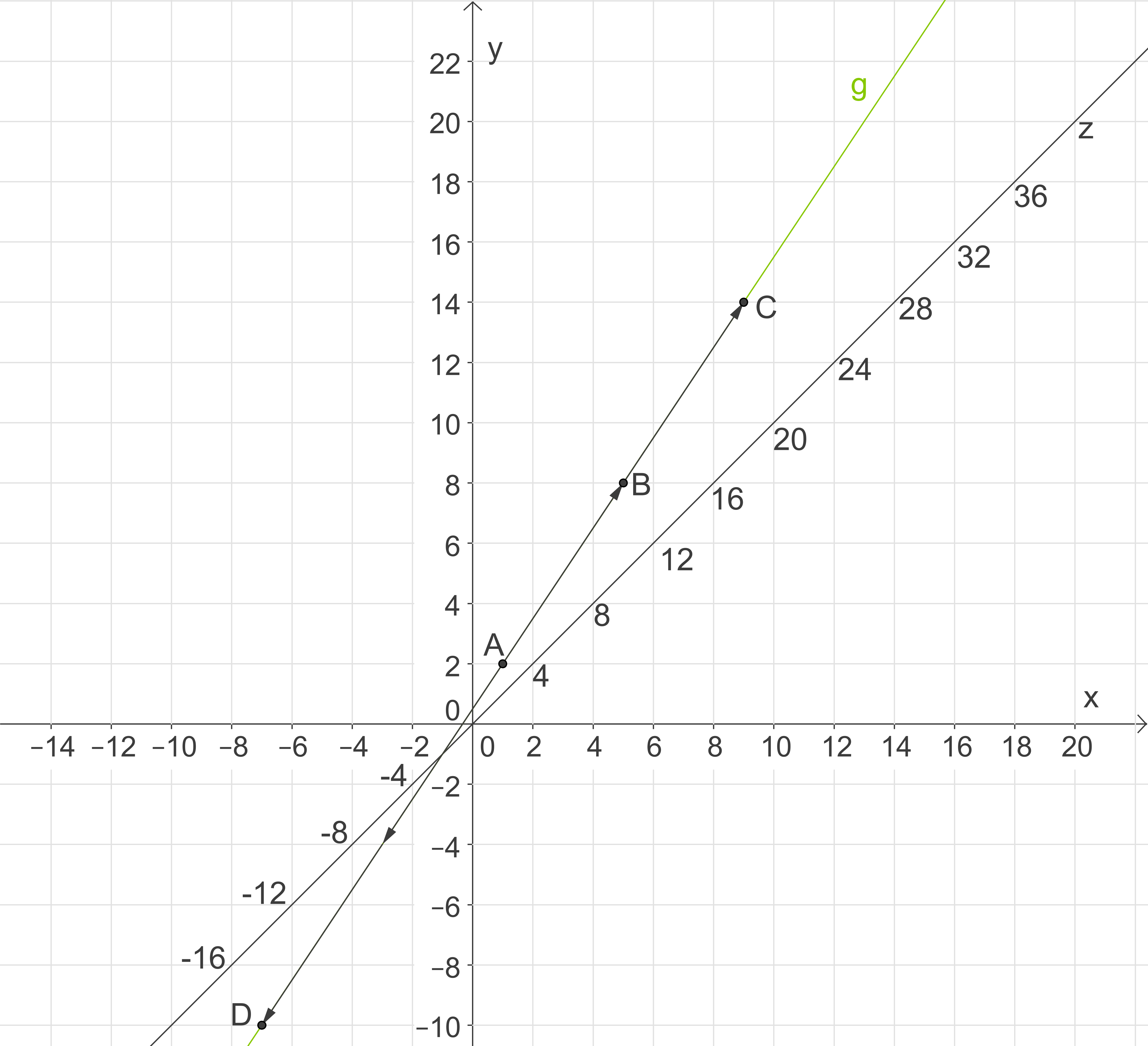Grafik einer linearen Funktion im Koordinatensystem mit Achsen und einer eingezeichneten Linie.

Der Verbindungsvektor $\overrightarrow{AB}$ lautet:

$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\begin{pmatrix}2\\5\\6\end{pmatrix}- \begin{pmatrix}0\\1\\2\end{pmatrix}=\begin{pmatrix}2\\4\\4\end{pmatrix}$ .

Damit ergeben sich $\overrightarrow{OC}$ und $\overrightarrow{OD}$ :

$\overrightarrow{OC}=\overrightarrow{OA}+2\cdot \overrightarrow{AB}=\begin{pmatrix}0\\1\\2\end{pmatrix}+2\cdot\begin{pmatrix}2\\4\\4\end{pmatrix} =\begin{pmatrix}4\\9\\10\end{pmatrix}$ ,

$\overrightarrow{OD}=\overrightarrow{OA}+2\cdot \overrightarrow{AB}=\begin{pmatrix}0\\1\\2\end{pmatrix}-2\cdot\begin{pmatrix}2\\4\\4\end{pmatrix} =\begin{pmatrix}-4\\-7\\-6\end{pmatrix}$ .

Die Koordinaten lauten $C\left(4 \mid 9 \mid 10\right)$ und $D\left(-4 \mid -7 \mid -6\right)$ .

b) $\blacktriangleright$ Möglichkeiten für die Koordinaten des vierten Eckpunktes angeben

Ein Parallelogramm ist ein Viereck, bei dem gegenüberliegenden Seiten gleich lang und parallel sind. Damit ergeben sich für den gesuchten vierten Punkt mehrere Möglichkeiten. Eine Skizze kann hier hilfreich sein:

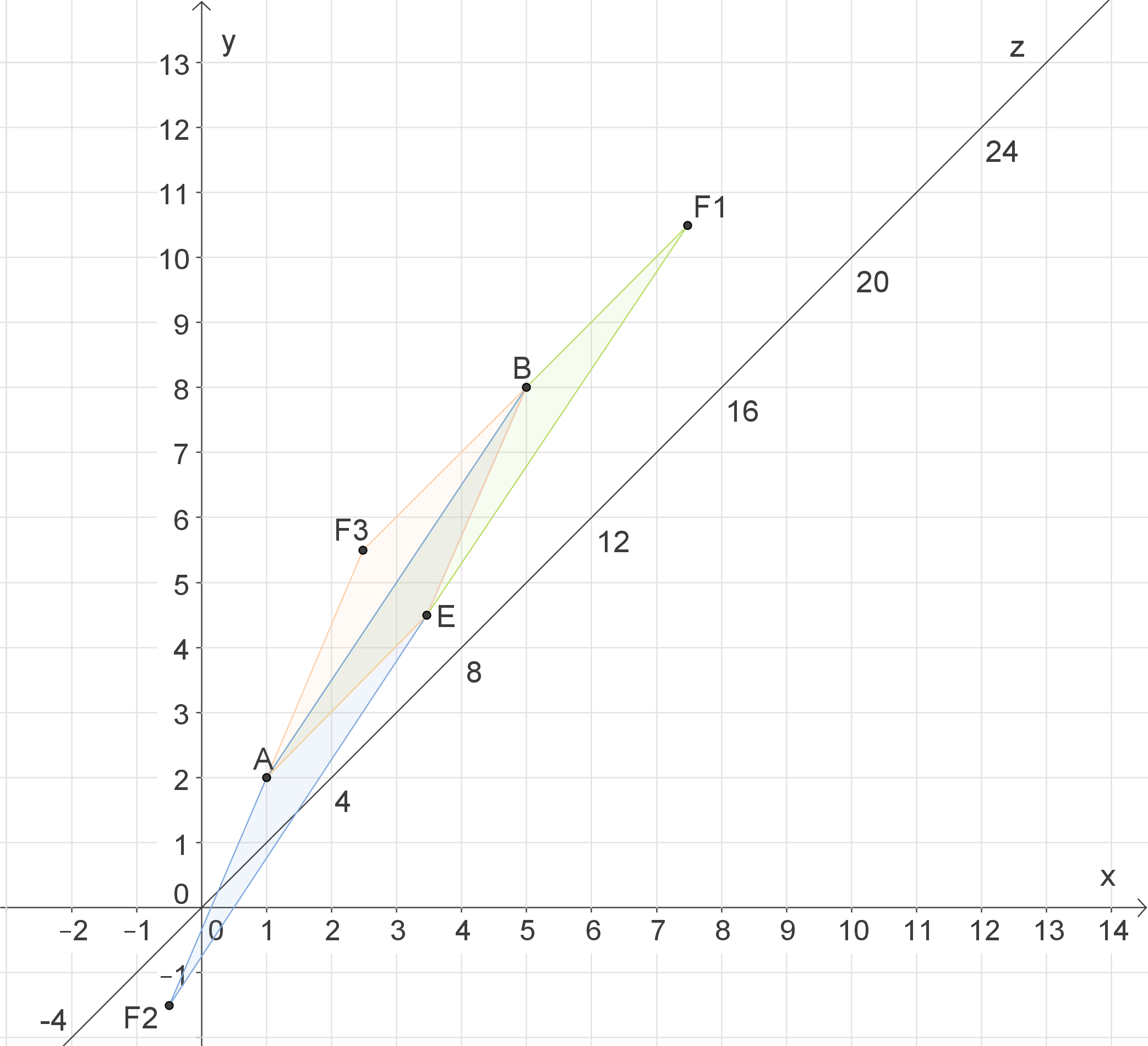
3D-Diagramm mit farbigen Flächen und Achsenbeschriftungen in einem Koordinatensystem.

$F_1$ , $F_2$ und $F_3$ geben an, wo ein solcher Punkt liegen könnte.

Durch Addieren des Verbindungsvektors $\overrightarrow{AB}$ zum Ortsvektor $\overrightarrow{OE}$ kann man $F_1$ erhalten. $F_2$ ergibt sich durch Subtraktion. $F_3$ kannst du erhalten, indem du den Verbindungsvektor $\overrightarrow{AE}$ von $\overrightarrow{OB}$ subtrahierst. Diese Möglichkeiten ergeben Parallelogramme, da durch das Addieren oder Subtrahieren eines Verbindungsvektors zweier Eckpunkte von dem dritten Eckpunkt folgt, dass die gegenüberliegenden Seiten des entstehenden Vierecks parallel und gleich lang sind.

Du erhältst:

$\overrightarrow{OF_1}=\overrightarrow{OE}+\overrightarrow{AB}=\begin{pmatrix}1\\2\\5\end{pmatrix} +\begin{pmatrix}2\\4\\4\end{pmatrix}=\begin{pmatrix}3\\6\\9\end{pmatrix}$ ,

$\overrightarrow{OF_2}=\overrightarrow{OE}-\overrightarrow{AB}=\begin{pmatrix}1\\2\\5\end{pmatrix} -\begin{pmatrix}2\\4\\4\end{pmatrix}=\begin{pmatrix}-1\\-2\\1\end{pmatrix}$ ,

$\overrightarrow{OF_3}=\overrightarrow{OB}-\overrightarrow{AE}=\begin{pmatrix}2\\5\\6\end{pmatrix} -\begin{pmatrix}1\\1\\3\end{pmatrix}=\begin{pmatrix}1\\4\\3\end{pmatrix}$ .

Mögliche Koordinaten des vierten Eckpunktes sind $F_1\left(3 \mid 6 \mid 9\right)$ , $F_2\left(-1 \mid -2 \mid 1\right)$ oder $F_3\left(1 \mid 4 \mid 3\right)$ .

Aufgabe P5

a) (1) $\blacktriangleright$ Übergangsgraph vervollständigen

Um den Übergangsgraphen zu vervollständigen, ist es wichtig, die Bedeutung dessen zu verstehen. Ein Pfeil des Übergangsgraphes gibt an, wieviele Kunden im nächsten vom einem Anbieter zum anderen wechseln. Die Pfeilspitze zeigt dabei an, wohin die Kunden wechseln.

Die angegebene Übergangstabelle gibt dir die erwartete Kundenwanderung für das nächste Jahr an. Mit Hilfe von dieser und der Gesamtanzahl von $10.000$ kannst du den Übergangsgraphen vervollständigen.

Konkret fehlen die Angaben für den Pfeil von $A3$ nach $A1$ und nach $A2$ . Berechne, wieviele Kunden vom Anbieter $A3$ zu dem Anbieter $A1$ oder $A2$ wechseln:

Nach der Übergangstabelle wechseln $0,02 \cdot 10.000=200$ Kunden von $A3$ zu $A1$ und $0,03 \cdot 10.000=300$ Kunden von $A3$ zu $A2$ . Damit ergibt sich der vollständige Übergangsgraph:

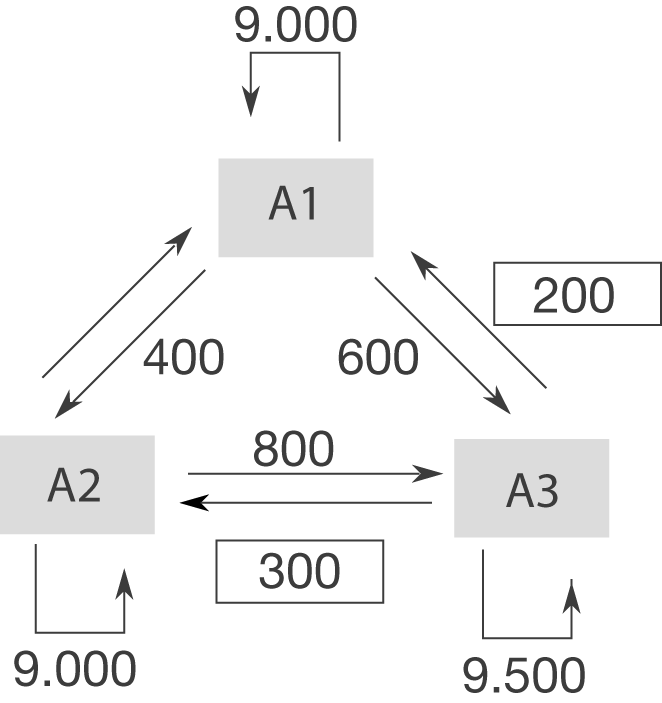Diagramm mit Knoten A1, A2 und A3, verbunden durch Zahlen und Pfeile, die verschiedene Werte anzeigen.

a) (2) $\blacktriangleright$ Gesamtanzahl der Anbieter wechselnden Kunden berechnen

Die Gesamtanzahl der innerhalb des nächsten Jahres wechselnden Kunden erhältst du, indem du die Anzahl aller Kunden, die wechseln, aufsummierst. Dies entspricht der Summe aller Werte von den geraden Pfeilen im Übergangsgraphen:

$400+200+800+300+200+600=2.500$

Die Gesamtanzahl der Kunden, die innerhalb des nächsten Jahres den Anbieter wechseln, beträgt $2.500$ .

b) (1) $\blacktriangleright$ Übergangsgraph vervollständigen

Der neue Übergangsgraph beschreibt nun die Kundenwanderung innerhalb des nächsten Jahres für die Anbieter $A1$ & $A2$ und $A3$ . Die gesuchten Werte ergeben sich aus dem Übergangsgraphen aus Teilaufgabe a), indem man dort Anbieter $A1$ und $A2$ zu einem Anbieter $A1$ & $A2$ zusammenfasst.

Die Anzahl der beim Anbieter $A3$ bleibenden Kunden kann direkt übernommen werden, da diese nicht von der Fusionierung beeinflusst sind:

$9.500$ .

Durch Addition der Kunden, die von $A1$ oder $A2$ zu $A3$ wechseln, erhält man die Anzahl der Kunden, die von $A1$ & $A2$ zu $A3$ wechseln:

$600 + 800 = 1.400$ .

Die Anzahl der Kunden, die bei $A1$ & $A2$ bleiben, erhältst du durch Addition der Kunden, die entweder bei $A1$ oder $A2$ bleiben oder zwischen den Anbietern $A1$ und $A2$ wechseln:

$9.000+400+200+9.000=18.600$ .

Damit ergibt sich der neue Übergangsgraph:

Diagramm mit den Bezeichnungen A1&A2 und A3 sowie verschiedenen Zahlenwerten und Pfeilen.

b) (2) $\blacktriangleright$ Übergangstabelle vervollständigen

Die neue Übergangstabelle, die wieder die erwartete Kundenwanderung für das nächste Jahr angibt, kannst du mit Hilfe des neuen Übergangsgraphen vervollständigen:

Da laut Aufgabenstellung jeder Anbieter eine Ausgangsverteilung von $10.000$ Kunden besitzt, zählt der fusionierte Anbieter $A1$ & $A2$ $2 \cdot 10.000=20.000$ Kunden zu Beginn. Von diesen bleiben $18.600$ beim fusionierten Anbieter und es ergibt sich für die erwartete Kundenwanderung von $A1$ & $A2$ zu $A1$ & $A2$ :

$\dfrac{18.600}{20.000}=\dfrac{93}{100}=0,93$ .

Von $A1$ & $A2$ wechseln $1.400$ der $20.000$ Kunden zum Anbieter $A3$ . Daraus folgt für die erwartete Kundenwanderung von $A1$ & $A2$ zu $A3$ :

$\dfrac{1.400}{20.000}=\dfrac{7}{100}=0,07$ .

$500$ der $10.000$ anfänglichen Kunden wechseln innerhalb des nächsten Jahres von $A3$ zu $A1$ & $A2$ und die erwartete Kundenwanderung von $A3$ zu $A1$ & $A2$ ergibt sich damit:

$\dfrac{500}{10.000}=\dfrac{5}{100}=0,05$ .

Somit kannst du die neue Übergangstabelle vervollständigen:

nach \ von	$\boldsymbol{A1}$ & $\boldsymbol{A2}$	$$ \boldsymbol{A3} $$
$\boldsymbol{A1}$ & $\boldsymbol{A2}$	$0,93$	$0,05$
$$ \boldsymbol{A3} $$	$0,07$	$0,95$