Analysis

Aufgabe 1A

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_k$ mit $f_k(x)=\tfrac{1}{2k}\cdot x^2\cdot (x-2k)^2$ und $k\in\mathbb{R}^+.$ Der Graph von $f_k$ wird mit $G_k$ bezeichnet.

Ohne Nachweis kannst du verwenden:
$\(f$ und $F_k(x)=\frac{1}{10k}x^5-\frac{1}{2}x^4+\frac{2k}{3}x^3$

Zeige, dass $x=0,$ $x=k$ und $x=2k$ für jeden Wert von $k$ Stellen mit waagerechter Tangente von $G_k$ sind.

(3 BE)

Der Hochpunkt von $G_k$ hat zu den beiden Tiefpunkten von $G_k$ denselben Abstand.

Berechne diesen Abstand.

(4 BE)

Betrachtet wird die Fläche, die $G_k,$ die $x$ -Achse und die beiden Geraden mit den Gleichungen $x=-1$ und $x=1$ einschließen. Sie setzt sich aus mehreren Flächenstücken zusammen.

Beurteile die folgende Aussage, ohne den Wert eines Integrals zu berechnen:

Für jeden Wert von $k$ gibt der Term $\displaystyle\int_{-1}^{1}f_k(x)\;\mathrm dx$ den Inhalt der betrachteten Fläche an.

(4 BE)

Betrachtet wird nun die Fläche zwischen $G_k$ und der $x$ -Achse im Intervall $[-k;k].$

Untersuche, ob die folgende Aussage richtig ist:

Für $k\gt2$ ist der Inhalt der Fläche kleiner als $k^5.$

(5 BE)

Um Regenwasser zu speichern, wird es kontrolliert in ein unterirdisches Auffangbecken geleitet. Für ein bestimmtes Regenereignis wird die momentane Zuflussrate des Regenwassers in das Auffangbecken durch die in $\mathbb{R}$ definierte Funktion $r$ mit $r(x)=\mathrm{e}^x\cdot f_{2,5}(x)$ für $0\leq x\leq5$ modellhaft beschrieben.

Dabei ist $x$ die Zeit in Stunden, die seit Beginn des Zuflusses in das Auffangbecken vergangen ist, und $r(x)$ die momentane Zuflussrate in $\tfrac{\text{m}^3}{\text{h}}$ (Kubikmeter pro Stunde). Die Funktion $f_{2,5}$ ist die Funktion der Schar $f_k$ mit $k=2,5.$

Bestimme die größte und die kleinste momentane Zuflussrate im betrachteten Zeitraum.

(4 BE)

Im Intervall $[0;5]$ besitzt $r$ genau zwei Wendestellen $x_0$ und $x_1.$ Außerdem gilt $\(r$ und $\(r$ sowie $\(r$ und $\(r$

Beschreibe die Bedeutung des Wertes $\(r$ die sich aus diesen Informationen ergibt, im Sachzusammenhang.

(3 BE)

Abbildung 1 zeigt den Graphen von $r$ mit einigen Eintragungen.

Erläutere, dass mit diesen Eintragungen die folgende Aussage begründet werden kann:

$\displaystyle\int_{4}^{5}r(x)\;\mathrm dx\lt120$

Interpretiere diese Aussage im Sachzusammenhang.

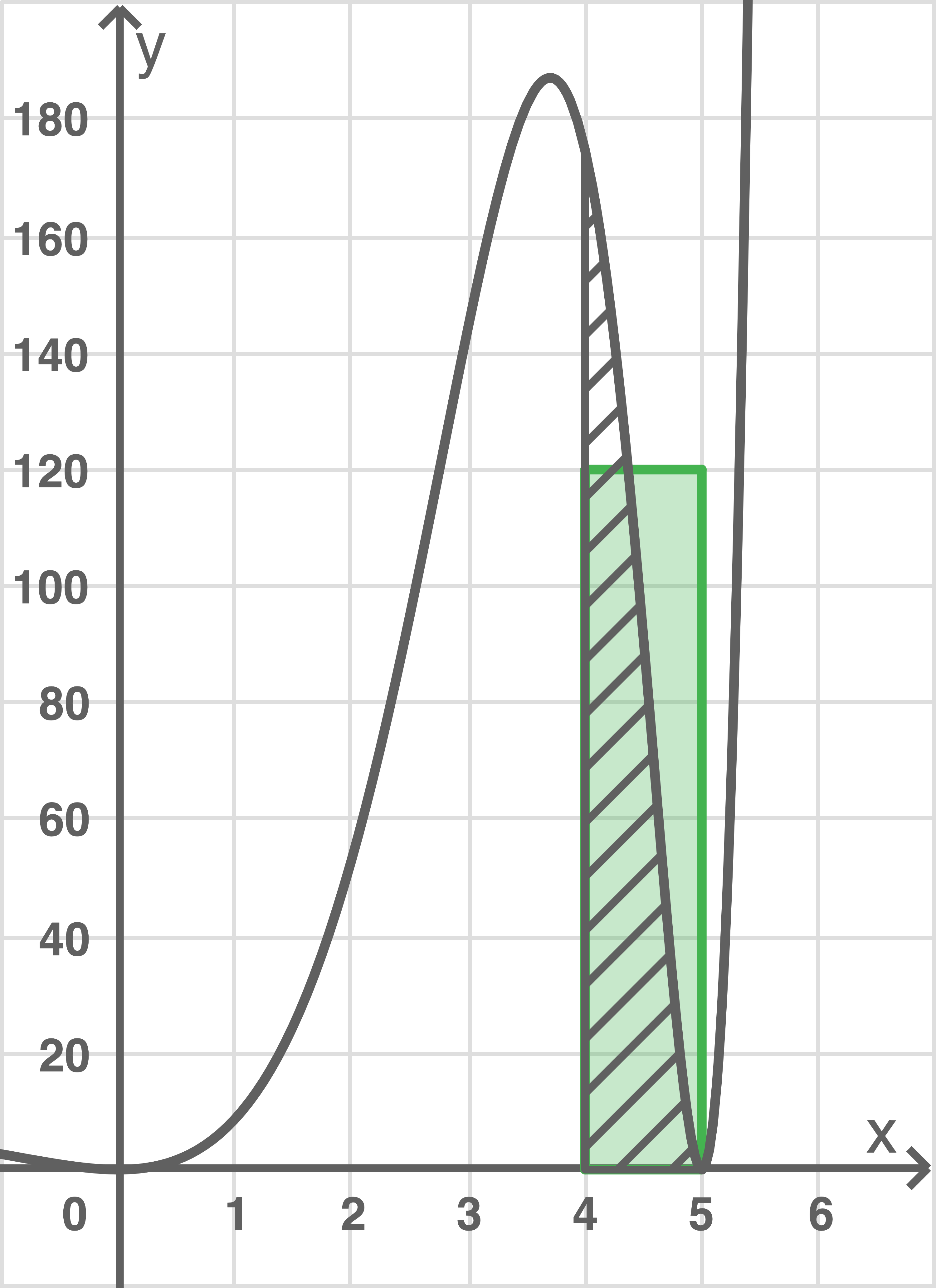
Graf einer Funktion mit gekennzeichnetem Bereich im Koordinatensystem.

Abbildung 1

(4 BE)

Zu Beginn des Zuflusses ist das Auffangbecken bereits mit $186\;\text{m}^3$ Regenwasser gefüllt. Nach dreieinhalb Stunden wird eine Pumpe eingeschaltet. Diese pumpt bis zum Ende des betrachteten Zeitraums Wasser aus dem Auffangbecken mit einer konstanten Rate ab. Die momentane Zuflussrate des Regenwassers in das Auffangbecken wird dabei weiterhin durch $r$ beschrieben.

Gib einen Term an, der das Wasservolumen im Auffangbecken zu einem beliebigen Zeitpunkt nach dem Einschalten der Pumpe in Kubikmetern beschreibt.

(3 BE)

Aufgabe 1B

Einige reetgedeckte Häuser haben Dachfenster in der Form einer sogenannten Fledermausgaube.
Abbildung 1 zeigt beispielhaft eine solche Fledermausgaube.
Abbildung 2 zeigt die obere Profillinie einer bestimmten Fledermausgaube, die durch die Funktion $f$ mit $f(x)=0,025x^4-0,3x^2+0,9$ und $n_1\leq x\leq n_2$ beschrieben wird.

Die $x$ -Achse stellt zwischen den Nullstellen $n_1$ und $n_2$ von $f$ den unteren Rand der Fledermausgaube dar. Alle Koordinaten haben die Einheit Meter $(\text{m}).$

Abbildung 1

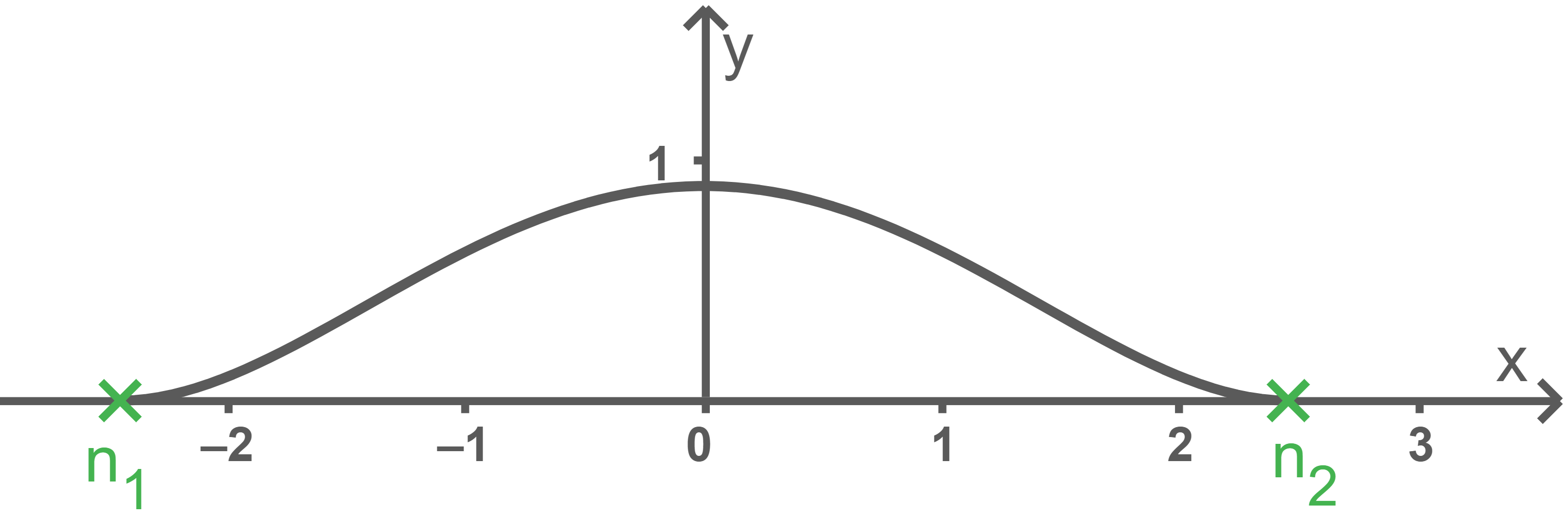
Modellierung Funktion Profillinie Reetdach Fledermausgaube

Abbildung 2

Ein rechteckiges Fenster soll in die Fledermausgaube eingepasst werden.

Bestimme die maximale Höhe, die ein solches $2\;\text{m}$ breites Fenster haben kann.

(2 BE)

Das Verhältnis von Breite zu Höhe soll bei Fledermausgauben zwischen $5:1$ und $8:1$ liegen.

Untersuche, ob die Vorgabe bei der betrachteten Fledermausgaube eingehalten wird.

(4 BE)

Aus ästhetischen Gründen soll die maximale Steigung der Profillinie einer Fledermausgaube $30^\circ$ betragen.

Weise nach, dass dies bei der betrachteten Fledermausgaube erfüllt ist.

(4 BE)

Ein zweiteiliges Fenster soll so in die Fledermausgaube eingepasst werden, dass der obere Rand der zwei Fensterscheiben $10\;\text{cm}$ unterhalb der oberen Profillinie und der untere Rand $10\;\text{cm}$ oberhalb des unteren Randes der Fledermausgaube liegt. Außerdem wird ein $10\;\text{cm}$ breiter Steg zwischen den beiden Fensterscheiben eingebaut. Abbildung 3 verdeutlicht die Situation.

Berechne den FIächeninhalt der beiden Fensterscheiben.

Abbildung 3

(6 BE)

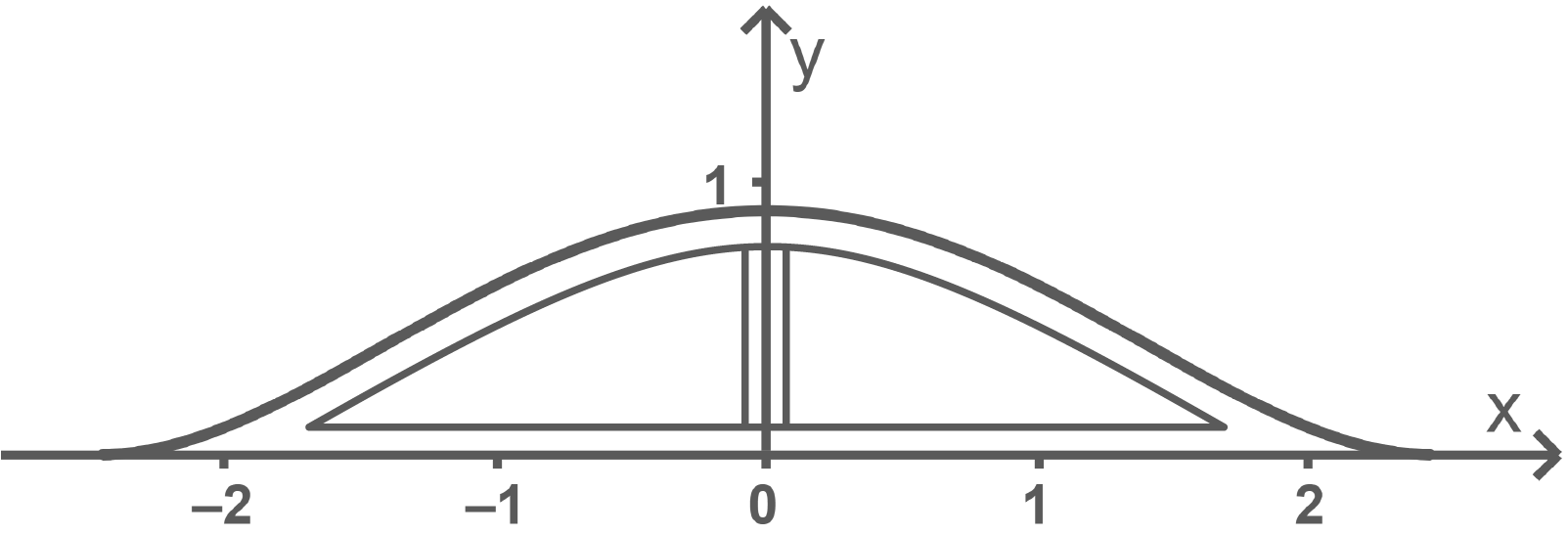
Ein dreieckiges Fenster in Form eines gleichschenkligen Dreiecks soll so eingebaut werden, dass die Basis des Dreiecks durch den unteren Rand der Fledermausgaube beschrieben wird und das Fenster an seiner höchsten Stelle $0,9\;\text{m}$ hoch ist.

Begründe, dass das Fenster nicht über die gesamte Breite des unteren Randes der Fledermausgaube verlaufen kann.

Bestimme den maximalen Flächeninhalt des Fensters.

(8 BE)

Die obere Profillinie der betrachteten Fledermausgaube kann für $n_1\leq x\leq n_2$ auch durch eine Funktion $g$ modelliert werden. Die Modellierung der oberen Profillinie durch beide Funktionen $f$ und $g$ ist in Abbildung 4 dargestellt.

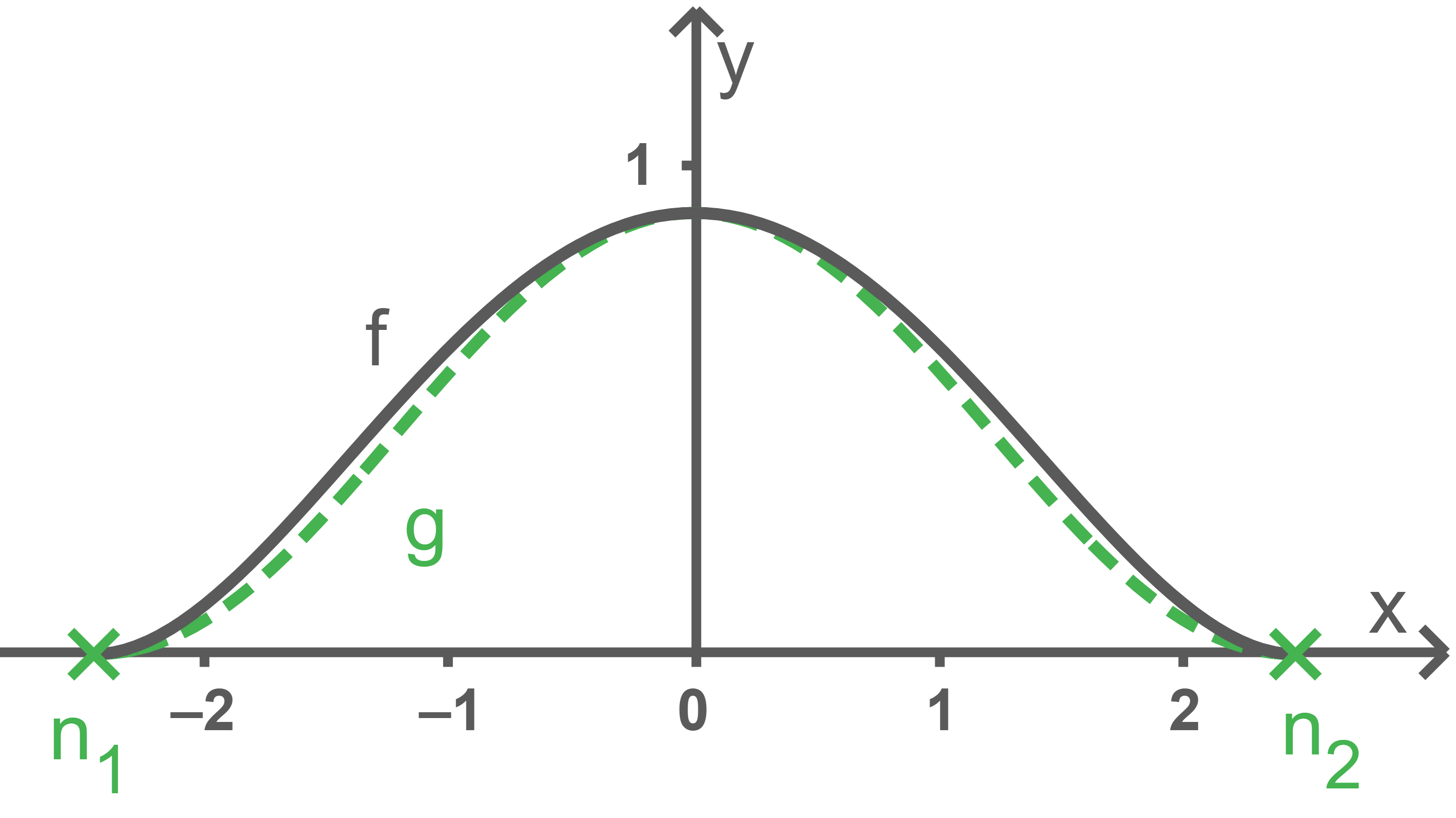
Modellierung Fledermausgaube zwei Funktionen

Abbildung 4

Gegeben ist die folgende Dokumentation einer Aufgabe:

$\text{I}.$ $f(x)-g(x)=d(x),$ wobei
$d(x)\geq0$ gilt.

$\text{II}.$ Für $n_1\leq x\leq0$ liefert $\(d$ die
Lösungen $x_1=n_1$ und $x_2\approx-1,38$
und $x_3=0.$

$\text{III}.$ $\(d$

$\text{IV}.$ $d(n_1)=0;\;d(x_2)\approx0,06;\;d(0)=0$

Erläutere die Schritte der Berechnung und gib die Bedeutung von $d(x_2)$ im Sachkontext an.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1A

Nach dem Satz des Nullprodukts ergeben sich die Nullstellen von $\(f_k$ durch die Nullstellen der einzelnen Faktoren der Funktionsgleichung.
Der Faktor $\frac{2}{k}$ wird für keinen Wert von $k$ Null, der Faktor $x$ besitzt die Nullstelle $x=0,$ der Faktor $x-k$ liefert direkt die Nullstelle $x=k,$ und der letzte Faktor $x-2k$ wird genau dann Null, wenn $x=2k$ gilt.
Da die Nullstellen von $\(f_k$ genau die Stellen sind, an denen $G_k$ eine waagerechte Tangente besitzt, sind $x=0, x=k$ und $x=2 k$ für jeden Wert von $k$ Stellen mit waagerechter Tangente.

Nach Teilaufgabe a) liefert die notwendige Bedingung von Extremstellen $\(f_k$ die folgenden Werte:

$\begin{array}[t]{rlll} x_1&=&0 \\[5pt] x_2&=&k \\[5pt] x_3&=&2k \end{array}$

Da zwischen zwei Tiefpunkten immer ein Hochpunkt liegen muss und insgesamt drei Extrempunkte vorliegen, folgt, dass $x_2=k$ zum Hochpunkt von $G_k$ gehört. Damit folgt für de gesuchten Abstand $d$ mit dem GTR:

$\begin{array}[t]{rlll} d&=&\sqrt{(k-0)^2+(f_k(k)-f_k(0))^2} \\[5pt] &=&\sqrt{k^2+(\dfrac{1}{2k}\cdot k^2\cdot(k-2k)^2-0)^2} \\[5pt] &=&k\cdot\sqrt{1+\dfrac{1}{4}k^4} \end{array}$

Der Funktionsterm von $f_k$ besteht aus drei Faktoren, wobei $\frac{1}{2k}$ für alle $k$ positiv ist da $k$ stets positiv ist, und die anderen beiden nicht negativ sind, da sie geradzahlige Exponenten besitzen. Somit verläuft $G_k$ nie unterhalb der $x$ -Achse, d.h. die Aussage aus der Aufgabenstellung stimmt.

Mit der graphischen Darstellung des GTR ergibt sich, dass $G_k$ im gesamten Intervall oberhalb der $x$ -Achse verläuft. Somit folgt für den gesuchten Flächeninhalt mit dem GTR:

$\begin{array}[t]{rlll} A&=&\displaystyle\int_{-k}^{k}f_k(x)\;\mathrm dx \\[5pt] &=&F_K(k)-F_k(-k) \\[5pt] &=&\dfrac{4}{15} k^4-\left(-\dfrac{19}{15} k^4\right) \\[5pt] &=&\dfrac{23}{15} k^4 \end{array}$

Damit folgt:

$\begin{array}[t]{rlll} \dfrac{23}{15} k^4&\lt&k^5 &\mid\;:k^4 \\[5pt] \dfrac{23}{15}&\lt&k \end{array}$

Da $\frac{23}{15}\lt2$ gilt, ist die Aussage aus der Aufgabenstellung somit richtig.

Die Funktion $r(x)$ ergibt sich als:

$r(x)=\mathrm e^x\cdot\dfrac{1}{5}x^2\cdot(x-5)^2$

Mit der Produktregel folgt für die Ableitung von $r:$

Rechenweg anzeigen

$\( r$

Die Notwendige Bedingung für Extremstellen $\(r$ liefert mit dem solve-Befehl des GTR für $0\leq x\leq5:$

$\begin{array}[t]{rlll} x_1&=&0 \\[5pt] x_2&=&\dfrac{1+\sqrt{41}}{2} \\[5pt] x_3&=&5 \end{array}$

Nach Teilaufgabe a) gilt $r(0)=0$ und $r(5)=0.$ Einsetzen von $x_2$ in $r(x)$ liefert:

Rechenweg anzeigen

$r\left(\dfrac{1+\sqrt{41}}{2}\right) \approx 187$

Da die Funktionswerte für sowohl $x_1$ als auch $x_3$ kleiner als $187$ sind, folgt, dass es sich bei $x_2$ um eine Hochstelle von $r$ handelt und zudem, dass $r$ an den Stellen $x=0$ und $x=5$ seinen im betrachteten Bereich minimalen Wert annimmt.

Die kleinste momentane Zuflussrate beträgt somit $0\;\frac{\text{m}^3}{\text{h}}$ und die größte ca. $187\;\frac{\text{m}^3}{\text{h}}.$

Der stärkste Anstieg der momentanen Zuflussrate im betrachteten Zeitraum ist durch $\(r$ pro Stunde gegeben.

Begründung der Aussage erläutern

Die in der Abbildung grün markierte Fläche ist ein Rechteck mit den Seitenlängen $1$ und $120$ und besitzt somit den Flächeninhalt $120.$ Zudem wird aus der Abbildung deutlich, dass die schraffierte Fläche, deren Inhalt dem Wert des in der Aufgabenstellung gegebenen Integrals entspricht, kleiner ist, als die grün markierte Fläche. Damit kann die Aussage aus der Aufgabenstellung begründet werden.

Aussage im Sachzusammenhang interpretieren

Innerhalb der letzten Stunde des betrachteten Zeitraums sind insgesamt weniger als $120\;\text{m}^3$ Regenwasser in das Auffangbecken geflossen.

Die Pumpe pumpt Wasser mit einer konstanten Rate ab. Wenn diese Rate mit $a$ bezeichnet wird, folgt für den gesuchten Term:

$186+\displaystyle\int_{0}^{x}r(t)\;\mathrm dt-a\cdot(x-3,5)$

Lösung 1B

Die Profillinie der Fledermausgaube ist symmetrisch zur $y$ -Achse mit einem Hochpunkt auf dieser. Somit liegt das Fenster mit der maximalen Höhe ebenfalls symmetrisch zur $y$ -Achse, d.h. zwischen $x=-1$ und $x=1.$ Für die Höhe folgt damit:

$\begin{array}[t]{rlll} f(1)&=&0,025\cdot1^4-0,3\cdot1^2+0,9 \\[5pt] &=&0,625\;[\text{m}] \end{array}$

Auflösen von $f(x)=0$ nach $x$ mit dem solve-Befehl des GTR liefert:

$\begin{array}[t]{rlll} x_1&\approx&-2,45 \\[5pt] x_2&\approx&2,45 \end{array}$

Die Breite der Gaube beträgt somit ca. $2,45-(-2,45)=4,9\;\text{m}.$ Für die Höhe der Gaube gilt ergibt sich $f(0)=0,9\;\text{m}$ mit dem GTR. Damit folgt:

$\dfrac{4,9}{0,9}\approx\dfrac{5,4}{1}$

Das Verhältnis ist somit ca. $5,4:1$ und damit wird die Vorgabe eingehalten.

Die vom Betrag her maximale Steigung der Profillinie liegt im Wendepunkt von $f$ vor. Für die ersten beiden Ableitungen von $f$ folgt:

$\(\begin{array}[t]{rlll} f$

Auflösen der notwendigen Bedingung $\(f$ nach $x$ liefert mit dem solve-Befehl des GTR:

$\begin{array}[t]{rlll} x_1&\approx&-1,41 \\[5pt] x_2&\approx&1,41 \end{array}$

Aus der Abbildung geht hervor, dass $f$ mindestens zwei Wendestellen besitzt, somit kann hier auf die Überprüfung der hinreichenden Bedingung verzichtet werden. Wegen der Symmetrie von $f$ zur $y$ -Achse ist der Betrag der Steigungen in $x_1$ und $x_2$ gleich, und es folgt:

$\(\begin{array}[t]{rlll} \tan(\alpha)&=&\vert f$

Auflösen nach $\alpha$ mit dem solve-Befehl des GTR liefert $\alpha\approx29,5^\circ$ für den gesuchten Winkel.

Der obere Rand des Fensters wird durch $f(x)-0,1$ beschrieben, während der untere Rand durch $y=0,1$ beschrieben wird. Gleichsetzen dieser beiden Funktionen liefert:

$\begin{array}[t]{rlll} f(x)-0,1&=&0,1 \\[5pt] 0,025x^4-0,3x^2+0,8&=&0,1 \end{array}$

Auflösen nach $x$ mit dem solve-Befehl des GTR liefert für die Eckpunkte der beiden Fensterscheiben:

$\begin{array}[t]{rlll} x_1&\approx&-1,78 \\[5pt] x_2&\approx&1,78 \end{array}$

Da in der Mitte ein $10\;\text{cm}$ breiter Steg eingebaut wird, verläuft die rechte Fensterscheibe zwischen $x=0,05$ und $x\approx1,78.$ Wegen der Symmetrie folgt somit für den Flächeninhalt beider Fensterscheiben:

Rechenweg anzeigen

$A \approx 1,47\;\text{m}^2$

Damit das Fenster über die gesamte Breite der Fledermausgaube verlaufen kann, muss die Strecke zwischen den Punkten $(0\mid0,9)$ und $(2,45\mid0),$ d.h. die Hypotenuse des dreieckigen Fensters, vollständig unterhalb des Graphen von $f$ liegen.Die graphische Darstellung des GTR zeigt aber, dass die Gerade teilweise auch oberhalb von von $f$ liegt. Somit geht das Fenster nicht über die gesamte Breite.
Der Flächeninhalt des Festers ist genau dann maximal, wenn das Fenster die Gaube in einem Punkt $(a\mid f(x))$ berührt, ohne sie zu schneiden, d.h. die Gerade die durch die Hypotenuse des Dreiecks definiert wird dort eine Tangente an $f$ ist. Für die Steigung der Tangente folgt damit:

$\(f$

Da das Fenster $0,9\;\text{m}$ hoch sein soll, ist der Achsenabschnitt der Tangente gegeben durch $0,9.$ Die Tangentengleichung ergibt sich somit als $t(x)=(0,1a^3-0,6a)x+0,9.$ Auflösen von $f(a)=t(a)$ nach $a$ mit dem solve-Befehl des GTR liefert:

$\begin{array}[t]{rlll} a_1&=&-2 \\[5pt] a_2&=&0 \\[5pt] a_3&=&2 \end{array}$

Da der rechte Teil der Gaube betrachtet wird, kommt nur $a_3=2$ infrage. Einsetzen in die Tangentengleichung liefert:

$\begin{array}[t]{rlll} t(x)&=&(0,1\cdot2^3-0,6\cdot2)x+0,9 \\[5pt] &=&-0,4x+0,9 \end{array}$

Auflösen von $t(x)=0$ nach $x$ mit dem GTR liefert:

$x=2,25$

In dieser Nullstelle liegt somit der dritte Eckpunkt des dreieckigen Fensters, und für den Flächeninhalt von diesem folgt:

$\begin{array}[t]{rlll} A&=&\dfrac{1}{2}\cdot2,25\cdot0,9 \\[5pt] &=&2,025\;[\text{m}^2] \end{array}$

Schritte der Berechnung erläutern

$\text{I}.$

Die Differenzenfunktion von $f$ und $g$ wird gebildet, wobei der Graph von $f$ für alle $x$ nicht unter dem von $g$ liegt.

$\text{II}.$

Die Differenzenfunktion wird auf mögliche Extremstellen im Bereich $n_1\leq x\leq0$ überprüft.

$\text{III}.$

Die hinreichende Bedingung für Extremstellen wird nun für die mögichen Extremstellen überprüft und zeigt, dass alle drei Stellen tatsächlich Extremstellen sind.

$\text{IV}.$

Die Funktionswerte der Extremstellen werden berechnet.

Bedeutung im Sachkontext angeben

Der Wert von $d(x_2)$ besagt, dass die maximale vertikale Entfernung der durch $f$ und $g$ beschriebenen Profillinien ca. $0,06\;\text{m}$ beträgt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?