Stochastik

Aufgabe 2A

Bei einer Naturkostkette besitzen die meisten Kundinnen und Kunden ein Konto für Online-Bestellungen. Im Folgenden werden ausschließlich diese Personen betrachtet.

$72\,\%$ der Personen sind jünger als $50$ Jahre. $18\,\%$ der Personen sind jünger als $50$ Jahre und wohnen nicht in einer Großstadt. Der Anteil der Personen, die in einer Großstadt wohnen, beträgt $75\,\%.$ Es soll davon ausgegangen werden, dass in einer zufälligen Auswahl von Personen die Anzahl derjenigen, die in einer Großstadt wohnen, binomialverteilt ist.

Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.

(3 BE)

Beurteile die folgende Aussage:

Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person in einer Großstadt wohnt und nicht jünger als $50$ Jahre ist, ist etwa halb so groß wie die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person entweder in einer Großstadt wohnt oder nicht jünger als $50$ Jahre ist.

(4 BE)

Es werden $160$ Personen zufällig ausgewählt.

Bestimme die Wahrscheinlichkeit dafür, dass weniger als drei Viertel dieser Personen in einer Großstadt wohnen.

(2 BE)

Eine Abfüllanlage der Naturkostkette füllt veganen Brotaufstrich in Gläser ab, auf denen als Füllmenge „ $250\;\text{g}$ “ aufgedruckt ist. Die tatsächliche Füllmenge kann jedoch von der auf dem Glas aufgedruckten Füllmenge abweichen. Um festzulegen, welche Abweichungen der tatsächlichen von der aufgedruckten Füllmenge toleriert werden, wird die sogenannte Minusabweichung verwendet. Bei einer aufgedruckten Füllmenge von $250$ Gramm beträgt die Minusabweichung $4,5$ Gramm.

Die Gläser können gemäß einer Richtlinie mit der in der Abbildung 1 dargestellten Füllmengenkennzeichnung versehen werden, wenn drei Bedingungen erfüllt sind. Diese können modellhaft wie folgt formuliert werden:

Abbildung 1

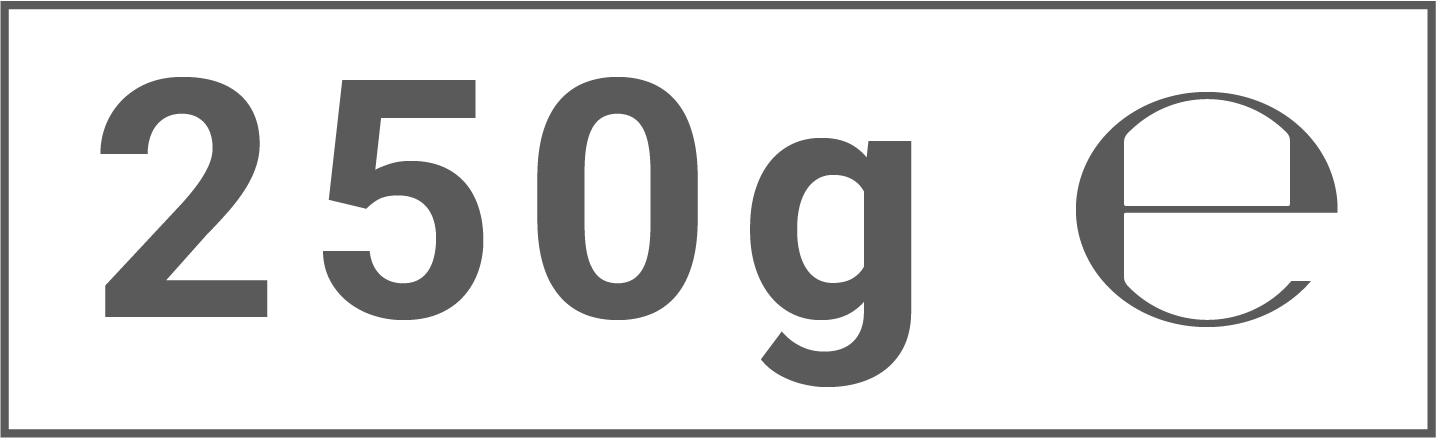
Die tatsächliche Füllmenge der Gläser in Gramm wird als Zufallsgröße betrachtet.

Bedingung I:	Der Erwartungswert der tatsächlichen Füllmenge in Gramm liegt nicht unter der aufgedruckten Füllmenge.
Bedingung II:	Die Wahrscheinlichkeit dafür, dass die tatsächliche Füllmenge in Gramm von der aufgedruckten Füllmenge um mindestens eine Minusabweichung nach unten abweicht, beträgt höchstens $6\,\%.$
Bedingung III:	Die Wahrscheinlichkeit dafür, dass die tatsächliche Füllmenge in Gramm von der aufgedruckten Füllmenge um mindestens zwei Minusabweichungen nach unten abweicht, beträgt höchstens $0,2\,\%.$

Die tatsächliche Füllmenge der Gläser in Gramm ist normalverteilt mit der Dichtefunktion $\varphi(x)=\tfrac{1}{2\sqrt{2\pi}}\cdot\mathrm{e}^{-\frac{1}{2}\cdot\left(\frac{x-250}{2}\right)^2},$ wobei $x$ die tatsächliche Füllmenge eines Glases in Gramm beschreibt.

Untersuche, ob jede der drei Bedingungen erfüllt ist.

(5 BE)

Eine weitere Produktion von Gläsern mit einer aufgedruckten Füllmenge von $250$ Gramm stammt von einer anderen Abfüllanlage für vegane Brotaufstriche. Die tatsächliche Füllmenge in Gramm ist normalverteilt mit den Parametern $\mu=250$ und $\sigma.$

Begründe, dass die folgende Aussage richtig ist:

Wenn diese Produktion die Bedingung II erfüllt, dann erfüllt sie auch die Bedingung III.

(6 BE)

Aufgabe 2B

Unter den Touristen eines Naturparks nutzen erfahrungsgemäß $14\,\%$ das Fahrrad für Ausflüge vor Ort. Im Folgenden werden diese Touristen als Radausflügler bezeichnet. Es soll davon ausgegangen werden, dass in einer zufälligen Auswahl von Touristen des Naturparks die Anzahl der Radausflügler binomialverteilt ist.
Für eine Stichprobe werden $300$ Touristen des Naturparks zufällig ausgewählt.

Bestimme die Wahrscheinlichkeit dafür, dass sich in der Stichprobe genau $36$ Radausflügler befinden.

(1 BE)

Ermittle die Wahrscheinlichkeit dafür, dass die Anzahl der Radausflügler in der Stichprobe um mindestens $10\,\%$ größer ist als der Erwartungswert für diese Anzahl.

(3 BE)

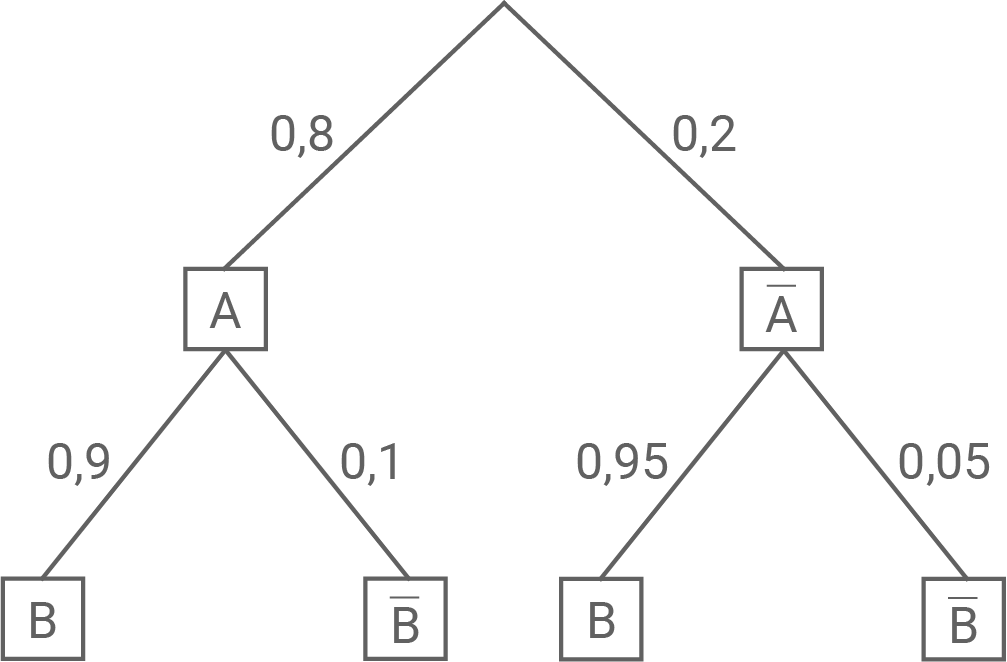
Um den Naturpark als Reiseziel attraktiver zu machen, setzt der dortige Tourismusverband Shuttlebusse ein. Die Fahrkarten für diese Busse können ausschließlich online gebucht werden und sind jeweils für einen bestimmten Tag gültig. Erfahrungsgemäß werden $80\,\%$ aller gebuchten Fahrkarten spätestens am Vortag der Fahrt gebucht. Von diesen spätestens am Vortag gebuchten Fahrkarten werden $90\,\%$ auch tatsächlich genutzt. Bei den restlichen, erst am Tag der Fahrt gebuchten Fahrkarten liegt der Anteil mit $95\,\%$ etwas höher.

Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 BE)

Betrachtet wird eine zufällig ausgewählte, nicht genutzte Fahrkarte.

Beurteile die folgende Aussage:

Die Wahrscheinlichkeit dafür, dass diese Fahrkarte spätestens am Vortag gebucht wurde, ist achtmal so groß wie die Wahrscheinlichkeit dafür, dass sie erst am Tag der Fahrt gebucht wurde.

(3 BE)

Der Tourismusverband vermutet, dass der Anteil der Radausflügler unter allen Touristen durch den Einsatz der Shuttlebusse nun $20\,\%$ beträgt. Um bei einer Sicherheitswahrscheinlichkeit von $90\,\%$ einen Schätzwert für den Anteil der Radausflügler unter den Touristen zu ermitteln, wird eine Stichprobe von $900$ zufällig ausgewählten Touristen betrachtet. Die Abbildung zeigt die Graphen der folgenden für $p\in[0;1]$ definierten Funktionen:

$g_1:p\mapsto p-1,64\cdot\sqrt{\dfrac{p\cdot(1-p)}{900}}$

$g_1:p\mapsto p+1,64\cdot\sqrt{\dfrac{p\cdot(1-p)}{900}}$

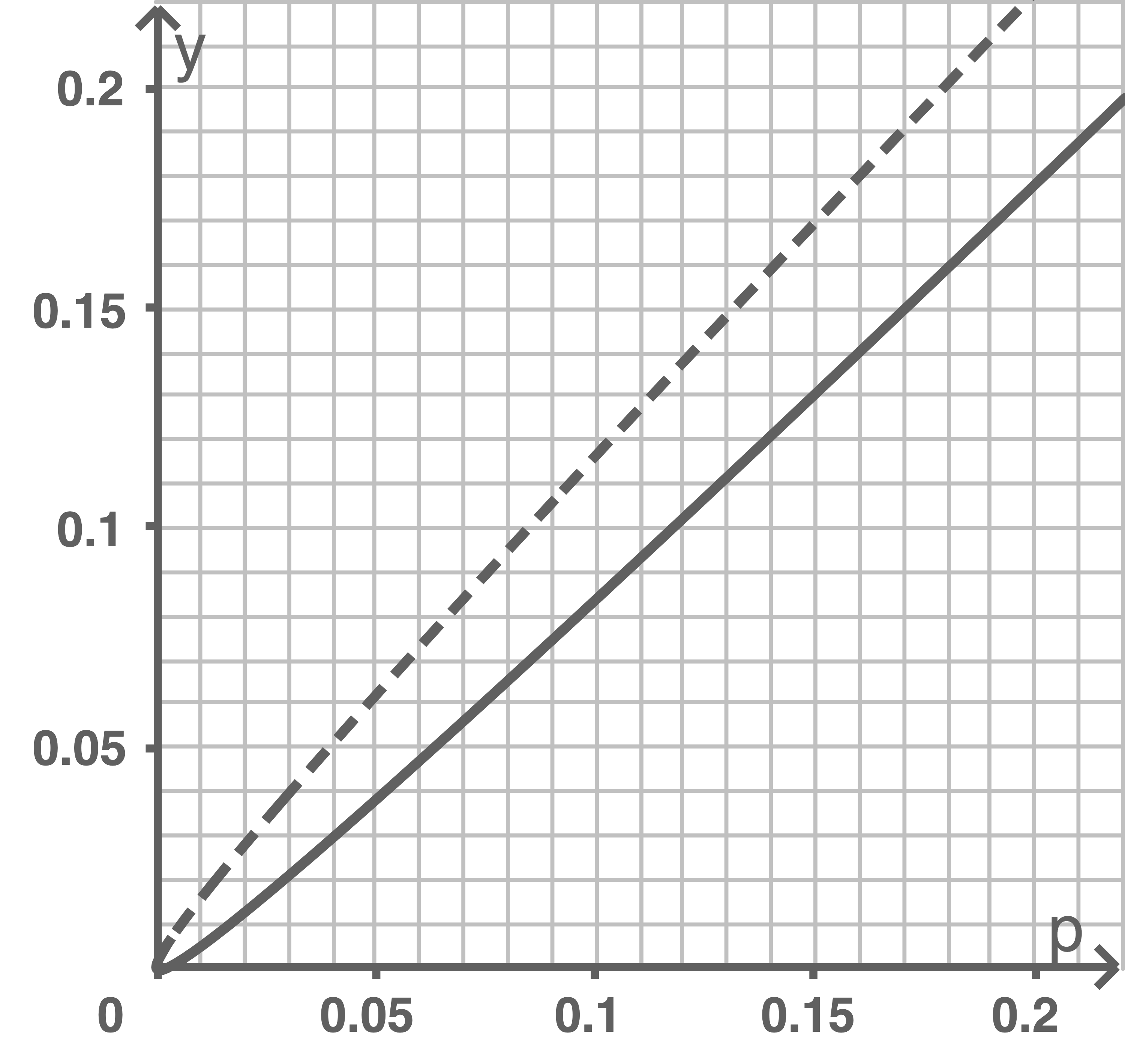
Diagramm mit zwei Linien auf einem Koordinatensystem, das Achsen für y und p zeigt.

Abbildung 1

In der Stichprobe werden $153$ Radausflügler gezählt.

Ermittle grafisch das zu dieser Anzahl gehörende Konfidenzintervall zur Sicherheitswahrscheinlichkeit $90\,\%$ und beurteile, ob die Vermutung des Tourismusverbandes mit dem Stichprobenergebnis verträglich ist.

(5 BE)

Betrachtet wird eine Stichprobe vom Umfang $n$ mit einem Anteil $h=0,17$ sowie das zu diesem Anteil gehörende Konfidenzintervall zur Sicherheitswahrscheinlichkeit $90\, \%.$

Betrachtet wird die folgende Aussage:

Der Wert $0,17$ liegt in der Mitte zwischen $0,14$ und $0,20.$ Trotzdem ist es möglich, dass die Annahme $p=0,14$ mit dem Stichprobenergebnis nicht verträglich ist, die Annahme $p=0,20$ hingegen schon.

Beurteile diese Aussage unter Verwendung der folgenden beiden Rechnungen:

$\begin{array}[t]{rlll} \text{I}.\quad0,17 &=& 0,14 + 1,64 \cdot\sqrt{\dfrac{0,14\cdot 0,86}{n}} \\[5pt] \Longrightarrow n &\approx& 359,8 \end{array}$

$\begin{array}[t]{rlll} \text{II}.\quad0,17 &=& 0,20 - 1,64 \cdot\sqrt{\dfrac{0,2\cdot 0,8}{n}} \\[5pt] \Longrightarrow n &\approx& 478,2 \end{array}$

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 2A

$J:$

„Die Person ist jünger als $50$ Jahre.“

$G:$

„Die Person wohnt in einer Großstadt.“

	$\color{#ffff}{J}$	$\color{#ffff}{\overline{J}}$
$\color{#ffff}{G}$	$0,54$	$0,21$	$0,75$
$\color{#ffff}{\overline{G}}$	$0,18$	$0,07$	$0,25$
	$0,72$	$0,28$	$1$

Für die Wahrscheinlichkeiten folgt mit der Vierfeldertafel:

$P\left(G\cap\overline{J}\right)=0,21$

$\begin{array}[t]{rlll} P(G\cap J)+P\left(\overline{G}\cap\overline{J}\right)&=&0,54+0,07 \\[5pt] &=&0,61 \end{array}$

Da $2\cdot0,21=0,42\neq0,61$ gilt, ist die Aussage falsch.

Die Zufallsvariable $X,$ die die Anzahl der Personen angibt die in einer wohnen, ist binomialverteilt mit $n=160$ und $p=P(G)=0,75.$ Damit folgt:

$\begin{array}[t]{rlll} P_{0,75}^{160}\left(X\lt\dfrac{3}{4}\cdot160\right)&=&P_{0,75}^{160}(X\lt120) \\[5pt] &=&P_{0,75}^{160}(X\leq119) \\[5pt] &\approx&0,4576 \\[5pt] &=&45,76\,\% \end{array}$

Aus der Dichtefunktion in der Aufgabenstellung kann abgelesen werden, dass die Zufallsvariable $Y,$ die die Füllmenge des Glases in Gramm angibt, normalverteilt mit den Parametern $\mu=250$ und $\sigma=2$ ist.
Da der Erwartungswert genau $250\;\text{g}$ beträgt, ist die Bedingung Ierfüllt. Mit dem GTR folgt zudem:

$\begin{array}[t]{rlll} P(Y\leq250-4,5)&=&P(Y\leq245,5) \\[5pt] &\approx&0,012 \\[5pt] &\lt&0,06 \end{array}$

$\begin{array}[t]{rlll} P(Y\leq250-2\cdot4,5)&=&P(Y\leq241) \\[5pt] &\approx&0,000003 \\[5pt] &\lt&0,002 \end{array}$

Somit sind auch Bedingungen II und III erfüllt.

Die Zufallsvariable $Y$ ist jetzt normalverteilt mit den Paramtern $\mu=250$ und unbekanntem $\sigma.$ Die Ungleichung $P(Y\leq145,5)\lt0,06$ liefert durch systematisches Ausprobieren mit dem GTR:

$\sigma\lt3$

Mit $\sigma=3$ ergibt sich:

$\begin{array}[t]{rlll} P(Y\leq241)&\approx&0,00135 \\[5pt] &\lt&0,002 \end{array}$

Da aus Bedingung II eigentlich $\sigma\lt3$ folgt, gilt sogar $P(Y\leq241)\lt0,00135.$ Da alle diese Werte immernoch kleiner als $0,002$ sind, ist somit, wenn für diese Produktion Bedingung II erfüllt ist, auch Bedingung III erfüllt.

Lösung 2B

Die Zufallsvariable $X,$ die die Anzahl der Radausflügler angibt, ist binomialverteilt mit $n=300$ und $p=0,14.$ Für die gesuchte Wahrscheinlichkeit folgt somit:

Rechenweg anzeigen

$P_{0,14}^{300}(X=36) \approx 4,2\,\%$

Für den Erwartungswert gilt:

$\mu=n\cdot p=300\cdot0,14=42$

Es gilt $42\cdot0,1=4,2$ und $42+4,2=46,2.$ Damit folgt für die gesuchte Wahrscheinlichkeit:

$\begin{array}[t]{rlll} P_{0,14}^{300}(X\geq46,2)&=&P_{0,14}^{300}(X\geq47) \\[5pt] &=&1-P_{0,14}^{300}(X\leq46) \\[5pt] &\approx&1-0,7757 \\[5pt] &=&0,2243 \\[5pt] &=&22,43\,\% \end{array}$

$A:$

„Die Fahrkarte wird spätestens am Vortag gebucht.“

$B:$

„Die Fahrkarte wird tatsächlich genutzt.“

$\begin{array}[t]{rlll} P_\overline{B}(A)&=& \dfrac{P\left(\overline{B}\cap A\right)}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,8\cdot0,1}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,08}{P\left(\overline{B}\right)} \end{array}$

$\begin{array}[t]{rlll} P_\overline{B}\left(\overline{A}\right)&=& \dfrac{P\left(\overline{B}\cap \overline{A}\right)}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,2\cdot0,05}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,01}{P\left(\overline{B}\right)} \end{array}$

Damit folgt:

$\begin{array}[t]{rlll} 8\cdot P_\overline{B}\left(\overline{A}\right)&=&8\cdot\dfrac{0,01}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,08}{P\left(\overline{B}\right)} \\[5pt] &=&P_\overline{B}(A) \end{array}$

Die Aussage aus der Aufgabenstellung ist somit richtig.

Es gilt $\dfrac{900}{153}=0,17.$ Damit ergibt sich die folgende Abbildung:

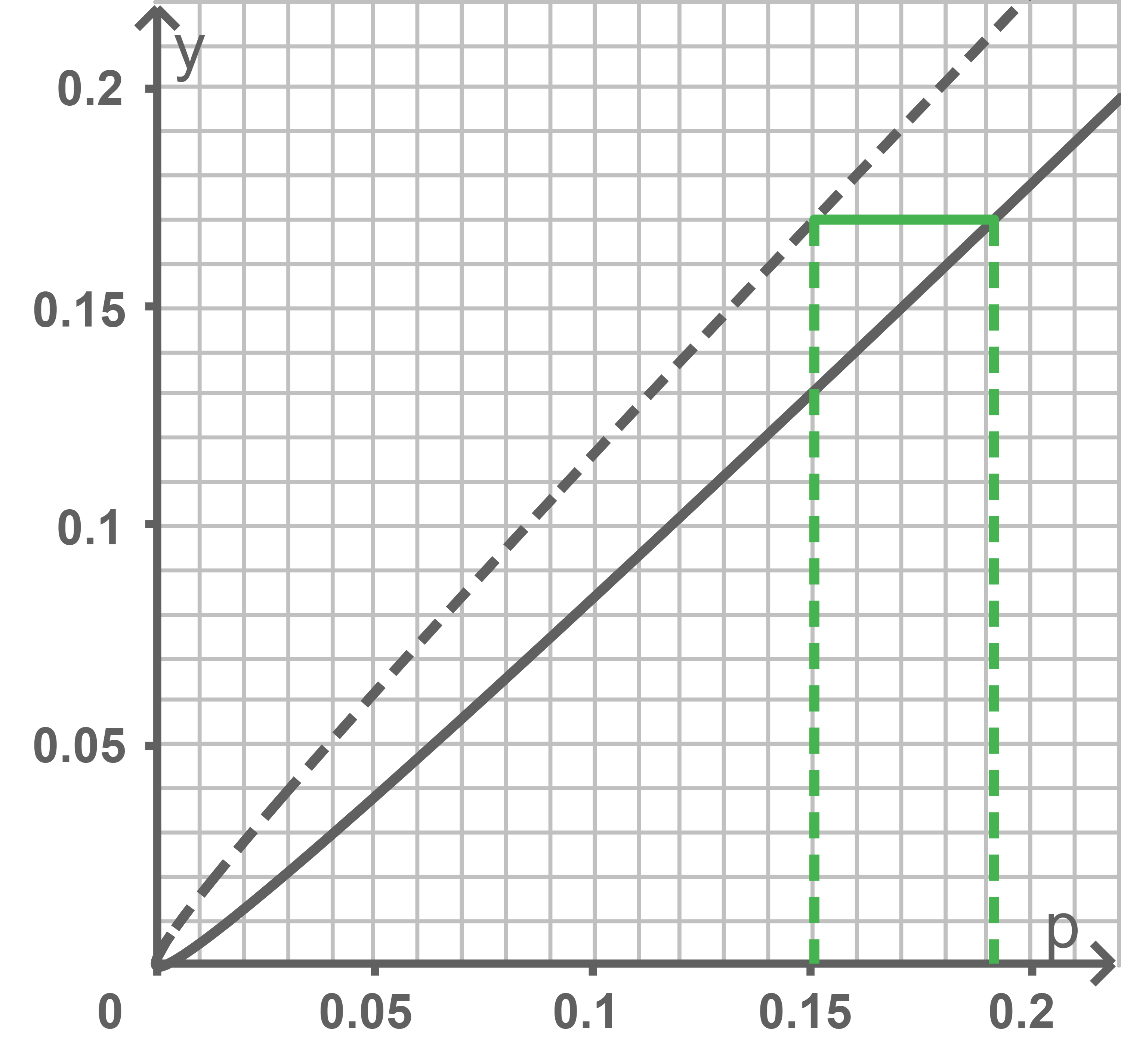
Diagramm mit Koordinatensystem, Linien und grünen Markierungen zur Veranschaulichung einer mathematischen Beziehung.

Das Konfidenzintervall ergibt sich in diesem Fall somit ungefähr als $[0,15;0,19].$ Da $0,2$ nicht in diesem Intervall liegt, ist die Vermutung des Tourismusverbandes nicht mit dem Stichprobenergebnis verträglich.

Rechnung $\text{I}$ liefert, dass die untere Grenze des Konfidenzintervalls für $n \geq 360$ größer als $0,14$ ist und Rechnung $\text{II},$ dass die obere Grenze des Konfidenzintervalls für $n \leq 478$ größer als $0,2$ ist.
Für alle Werte von $n$ zwischen $360$ und $478$ ist somit $p=0,2$ mit dem Stichprobenergebnis verträglich, $p=0,14$ aber nicht. Somit ist die Aussage korrekt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?