Anwendungsorientierte Analysis 2

Das Training einer Schwimmerin wird mit Videos ausgewertet. Die folgende Abbildung zeigt modellhaft die Geschwindigkeit $\text{v}$ der Schwimmerin in Metern $(\text{m})$ pro Sekunde $(\text{s})$ in Abhängigkeit von der Zeit $t$ in $s$ .
Ein Armzyklus dauert $1,2 \, \text{s}$ .

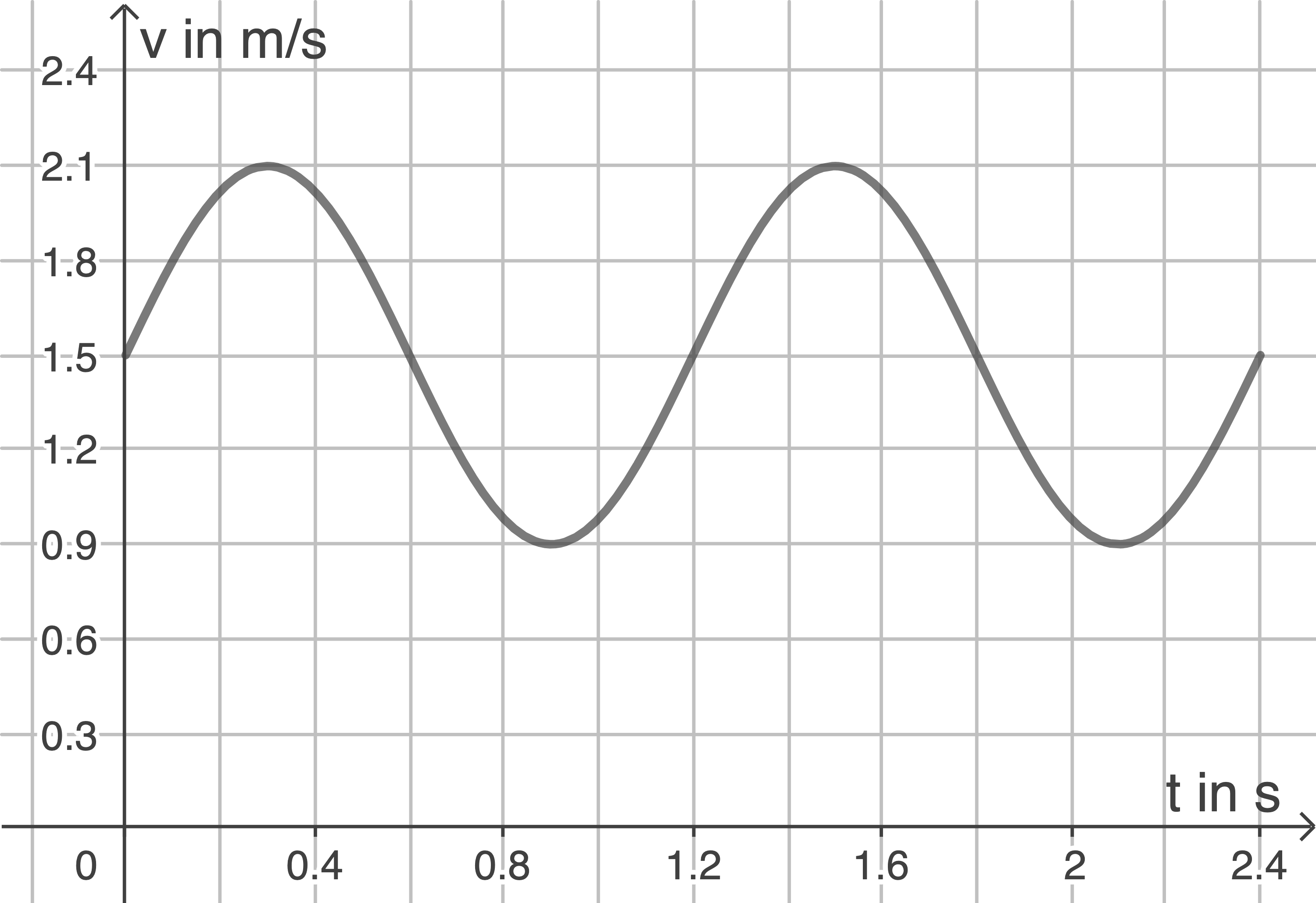
Grafik zeigt eine sinusförmige Kurve der Geschwindigkeit in m/s über die Zeit in Sekunden.

3.1

Begründe mit Hilfe der Abbildung, dass die Geschwindigkeit $\text{v}$ ab dem Beobachtungsbeginn $t=0$ durch die Funktionsgleichung $\text{v}(t)=1,5+0,6 \cdot \text{sin} \left(\dfrac{5\pi}{3}\cdot t\right)$ beschrieben werden kann.

3.2

Ermittle die Länge der Strecke, die gemäß des Modells während eines Armzyklus zurückgelegt wird.

Bestimme damit die Zeit, die die Schwimmerin für $36 \,\text{m}$ benötigt.

3.3

Zum Zeitpunkt $t=24$ beginnt die Schwimmerin ihren Endspurt. Dabei erhöht sich ihre Geschwindigkeit pro Sekunde zusätzlich um $0,05 \, \dfrac{\text{m}}{\text{s}}$ .
Die Geschwindigkeit der Schwimmerin ist in der Abbildung dargestellt und wird ab $t=24$ durch eine Funktion $\text{v}_E$ modelliert.

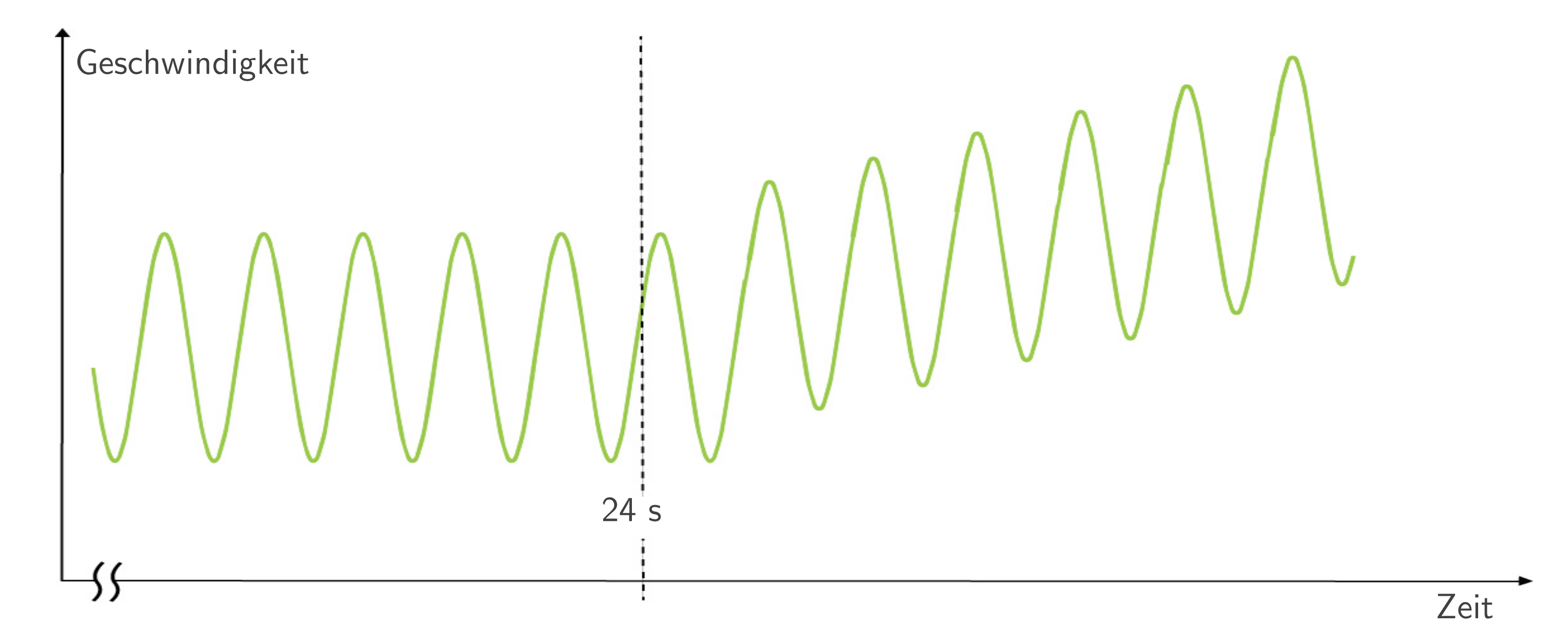
Diagramm zeigt eine sinusförmige Welle, die Geschwindigkeit über Zeit darstellt, mit einem Zeitintervall von 24 Sekunden.

3.3.1

Interpretiere den Ansatz $\displaystyle\int_{24}^{24+u}\text{v}_E(t)\;\mathrm dt=14$ im Sachzusammenhang.

3.3.2

Gib einen Funktionsterm für die Funktion $\text{v}_E$ an.