Vektorgeometrie 2
2
Die Punkte 
und 
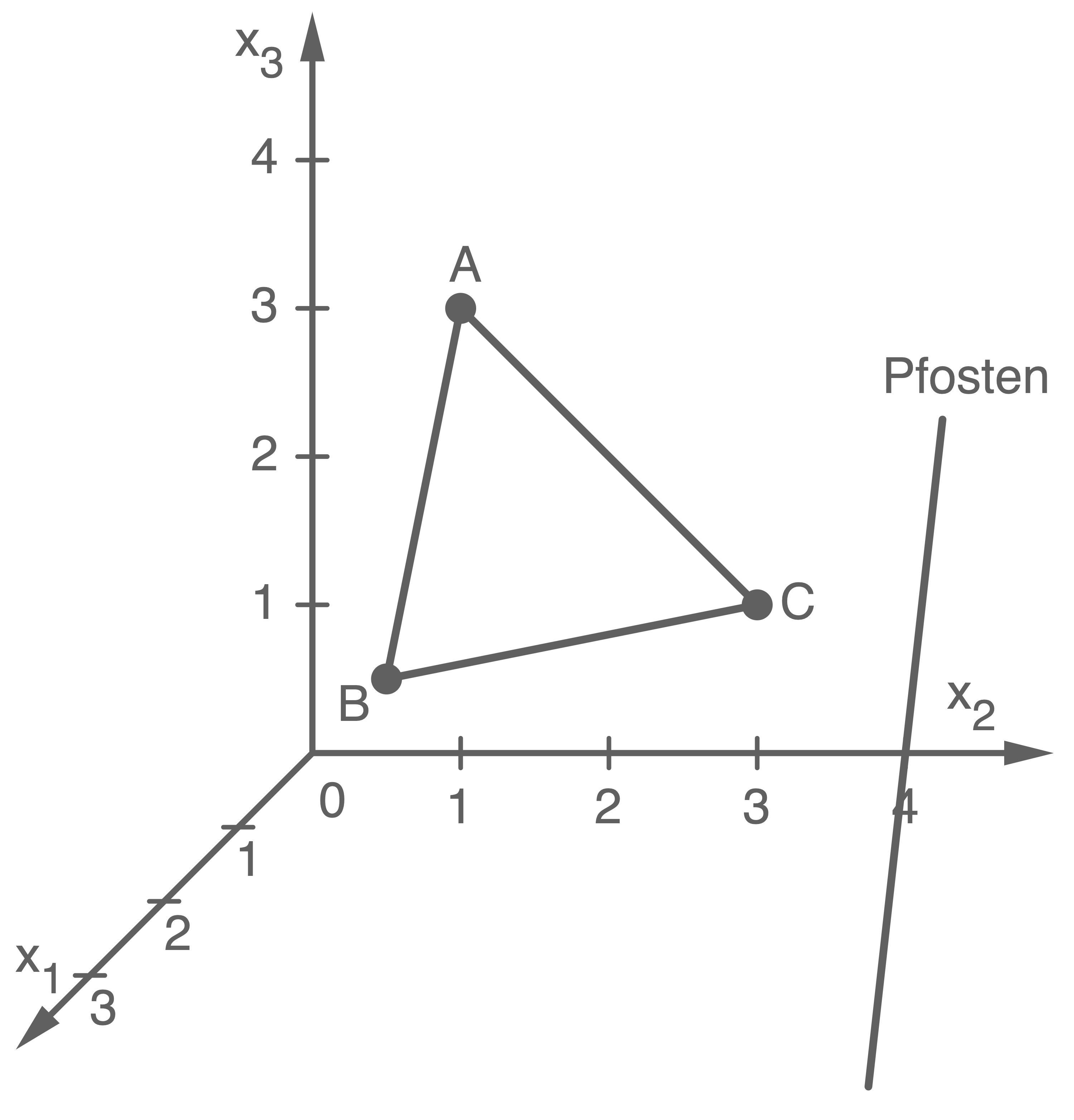
sind die Eckpunkte eines über dem Boden (
-Ebene) aufgespannten ebenen Sonnensegels.
Zur Befestigung dient unter anderem ein Pfosten, der sich durch die Strecke
beschreiben lässt. Eine Längeneinheit entspricht einem Meter.
2.1
Gib den kleinsten Abstand des Sonnensegels zum Boden an.
Zeige, dass das Sonnensegel in der Ebene mit der Gleichung
liegt.
Zeige, dass das Sonnensegel in der Ebene mit der Gleichung
3
2.2
Der für die Herstellung des Sonnensegels benötigte Stoff kostet 21 € pro Quadratmeter. Dabei fallen zum benötigten Flächeninhalt zusätzlich 
Verschnitt an.
Berechne die Kosten.
Berechne die Kosten.
3
2.3
Der Punkt 
ist mit einem Seil an dem Pfosten befestigt. Beurteile, ob ein Seil der Länge 
dafür ausreichend ist.
4
2.4
Robert blickt von Position 
aus in Richtung Sonne.
Das Sonnenlicht fällt aus der Richtung
ein.
Untersuche, ob Robert vom Sonnenlicht geblendet wird.
Das Sonnenlicht fällt aus der Richtung
Untersuche, ob Robert vom Sonnenlicht geblendet wird.
5
15
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1
Kleinsten Abstand zum Boden angeben
Da der Boden durch die 
-Ebene beschrieben wird, ist der Punkt mit dem kleinsten Abstand zum Boden der Punkt mit der betragsmäßig kleinsten 
-Koordinate.
Dies ist der Punkt 
Der kleinste Abstand des Sonnensegels zum Boden beträgt also zwei Meter.
Lage des Sonnensegels in der Ebene zeigen
Punktprobe mit 
Die Koordinaten von 
erfüllen die Ebenengleichung 
Der Eckpunkt liegt also in der Ebene.
Punktprobe mit 
Die Koordinaten von 
erfüllen die Ebenengleichung Der Eckpunkt liegt also in der Ebene.
Punktprobe mit 
Die Koordinaten von erfüllen die Ebenengleichung Der Eckpunkt liegt also in der Ebene.
Alle drei Eckpunkte des Sonnensegels liegen in der Ebene mit der Ebenengleichung Somit liegt das komplette Sonnensegel in dieser Ebene.
2.2
Das Sonnensegel hat die Form eines Dreiecks, das von den Vektoren 
und 
aufgespannt wird.
Mit dem Vektorprodukt kann der Flächeninhalt berechnet werden:![\(\begin{array}[t]{rll}
A_{ABC} &=&\frac{1}{2}\cdot \left|\overrightarrow{AB}\times\overrightarrow{AC} \right| \\[5pt]
&=& \frac{1}{2}\cdot \left|\pmatrix{1\\0\\-2}\times\pmatrix{2\\3\\-1} \right|\\[5pt]
&=& \frac{1}{2}\cdot \left|\pmatrix{0\cdot (-1) - (-2)\cdot 3 \\ -2\cdot 2 - 1\cdot (-1) \\1\cdot 3-0\cdot 2} \right|\\[5pt]
&=& \frac{1}{2}\cdot \left|\pmatrix{6 \\ -3 \\ 3} \right| \\[5pt]
&=& \frac{1}{2}\cdot \sqrt{6^2 +(-3)^2 +3^2}\\[5pt]
&=& \frac{1}{2}\cdot \sqrt{54}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/a8ade0fed98d9c4cf14e0f3c5b751826575fbe0f60f1fda4e5fc60f4037a195e?color=5a5a5a)
Für die benötigte Menge Stoff müssen zusätzlich Verschnitt einberechnet werden:
![\(\frac{1}{2}\cdot \sqrt{54} \cdot 1,1\,[\text{m}^2]\)](https://mathjax.schullv.de/1a2dad58c9e1399e2cc241de0846eca1caa1140fcd46c852130c268cc5563de0?color=5a5a5a)
Für die Kosten des Sonnensegels folgt:
Mit dem Vektorprodukt kann der Flächeninhalt berechnet werden:
2.3
1. Schritt: Funktion für die Seillänge aufstellen
Die Länge des Seils entspricht dem Abstand von zum Befestigungspunkt am Pfosten.
Die Punkte auf der Strecke, die den Pfosten beschreibt, haben die Koordinaten
mit 
Mit Hilfe der Abstandsformel zweier Punkte lässt sich daraus eine Funktion in Abhängigkeit von
aufstellen, die die Seillänge beschreibt:
2. Schritt: Seillänge überprüfen
Es muss überprüft werden, ob es ein 
gibt, für das 
ist:
Da für beide Lösungen gilt 
reicht eine Seillänge von aus.
Die Punkte auf der Strecke, die den Pfosten beschreibt, haben die Koordinaten
Mit Hilfe der Abstandsformel zweier Punkte lässt sich daraus eine Funktion in Abhängigkeit von
2.4
Robert wird nicht geblendet, wenn die Sonnenstrahlen, die in seine Richtung scheinen, vom Sonnensegel unterbrochen werden.
1. Schritt: Geradengleichung für die Sonnenstrahlen aufstellen
Die Sonnenstrahlen, die in Roberts Richtung scheinen, können durch eine Gerade beschrieben werden. Als Ortspunkt wird Roberts Position 
verwendet, als Richtungsvektor der Vektor der Sonnenstrahlen:
2. Schritt: Gleichung für das Sonnensegel aufstellen
Das Dreieck 
kann durch folgende Gleichung beschrieben werden:
![\(\begin{array}[t]{rll}
\overrightarrow{x}&=& \overrightarrow{OA} + p\cdot \overrightarrow{AB} + r\cdot \overrightarrow{AC}\\[5pt]
&=& \pmatrix{2\\2\\4} + p\cdot \pmatrix{1\\0\\-2} + r\cdot \pmatrix{2\\3\\-1}
\end{array}\)](https://mathjax.schullv.de/18cc6b51d925aa841839fd7e0581d54cdaf0d0e7db5d766e8752c0870cd2cdd1?color=5a5a5a)
Dabei gilt 
und 
3. Schritt: Schnittpunkt von Sonnenstrahlen und Sonnensegel überprüfen
Gleichsetzen:
Daraus ergibt sich folgendes lineares Gleichungssystem:
Aus 
folgt 
Einsetzen in die anderen beiden Gleichungen:
Aus 
folgt 
Einsetzen in 
![\(\begin{array}[t]{rll}
-2,5 &=& -2\cdot (4r-1)-5,5r \\[5pt]
-2,5 &=& -13,5r +2 &\quad \scriptsize \mid\;-2 \\[5pt]
-4,5 &=& -13,5r &\quad \scriptsize \mid\; :(-13,5)\\[5pt]
\frac{1}{3} &=& r \\[5pt]
r &=& \frac{1}{3}
\end{array}\)](https://mathjax.schullv.de/048f0c1c5105de450d78f066ec861289d2f935e38abb92a453ef44a88bfa89c6?color=5a5a5a)
Damit folgt für 
Da 
und 
gilt, trifft die Gerade der Sonnenstrahlen auf das Sonnensegel, sodass Robert nicht geblendet wird.