Wahlaufgaben

4 Stochastik

Bei einem Glücksspiel wird ein Pfeil auf die in Abbildung 1 dargestellte Scheibe geworfen. Es wird angenommen, dass jeder Pfeil die Scheibe trifft. Die Skalierung gibt den Radius der einzelnen Kreise (in Längeneinheiten) an.

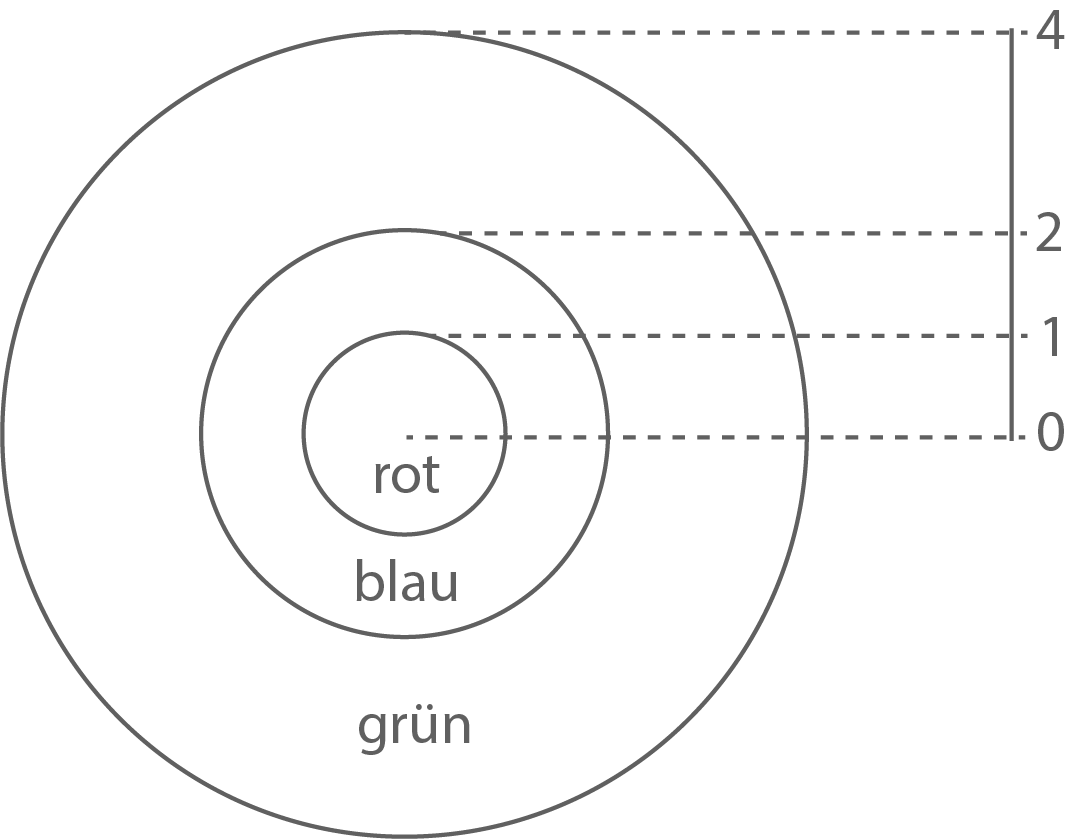
Diagramm mit drei konzentrischen Kreisen in den Farben rot, blau und grün, sowie einer Skala von 0 bis 4.

Abb. 1

Man trifft die unterschiedlich gefärbten Bereiche auf der Scheibe mit den folgenden Wahrscheinlichkeiten:

rot	blau	grün
$\dfrac{1}{16}$	$\dfrac{3}{16}$	$\dfrac{3}{4}$

Für das Glücksspiel gelten folgende Regeln:

Ein Spieler bezahlt einen Einsatz von $a$ Euro.
Je nach getroffener Farbe erhält der Spieler folgende Auszahlung:

Getroffene Farbe	Auszahlung
rot	$6$ Euro
blau	$2$ Euro
grün	$1$ Euro

Berechne den maximalen Einsatz $a,$ sodass der Spieler auf lange Sicht keinen Verlust macht.

(2 BE)

Der Flächeninhalt eines Kreises mit Radius $r$ beträgt $\pi \cdot r^2.$
Zeige, dass die oben gegebenen Wahrscheinlichkeiten dem Flächenanteil des jeweiligen Bereichs an der gesamten Kreisfläche entsprechen.

(3 BE)

4 Lineare Algebra

Gegeben sind die Punkte $A(4\mid2\mid-3), B(3\mid0\mid-1)$ und die Gerade $g,$ wobei $g: \overrightarrow{x}=\left(\begin{array}{c}3 \\ 0 \\ -1\end{array}\right)+r \cdot\left(\begin{array}{c}-2 \\ 4 \\ 3\end{array}\right), r \in \mathbb{R}.$

Zeige, dass der Abstand vom Punkt $A$ zur Geraden $g$ der Länge des Vektors $\overrightarrow{AB}$ entspricht.

(3 BE)

Ermittle die Koordinaten eines weiteren Punktes $C,$ der den gleichen Abstand zur Geraden $g$ hat wie der Punkt $A.$

(2 BE)

5 Stochastik

Ein Kartenspiel hat einen Kartensatz mit $32$ Karten: In jeder der vier Farben Kreuz (♣), Pik (♠), Herz (♥) und Karo (♦) gibt es jeweils ein Ass, einen König, eine Dame, einen Buben, eine $10,$ eine $9,$ eine $8$ und eine $7.$
Es wird eine Karte gezogen.

Bestimme die Wahrscheinlichkeit des folgenden Ereignisses:

Die gezogene Karte zeigt Karo oder ist eine Dame.

(2 BE)

Ein anderes Spiel hat einen Kartensatz, der nur aus $4$ Assen und $n$ Jokern besteht. Es wird zweimal ohne Zurücklegen eine Karte gezogen.
Die Wahrscheinlichkeit, zwei Asse zu ziehen, beträgt $\frac{2}{5}.$

Zeige, dass die Berechnung der Anzahl der Joker auf folgende Gleichung führt:

$2 n^2+14 n+24=60$

(3 BE)

5 Lineare Algebra

Gegeben ist das folgende lineare Gleichungssystem:

$\begin{array}[t]{rlll} x+y+z &=& 12 \\[5pt] 5x+10y+20z &=& 150 \end{array}$

Berechne die Lösungen des linearen Gleichungssystems, wenn $x, y$ und $z$ natürliche Zahlen sind.

(10 BE)

6 Analysis

(PLA; mit Hilfsmitteln)

Bearbeite die folgende Aufgabe unter Berücksichtigung der einzelnen Problemlöseschritte. Dokumentiere und reflektiere deine Vorgehensweise.

Gegeben sind folgende drei Eigenschaften, die eine Funktion $f$ bzw. deren Graph haben kann:

$f$ ist eine Polynomfunktion.
Der Graph von $f$ ist achsensymmetrisch zur $y$ -Achse.
Der Graph von $f$ besitzt mindestens einen Hochpunkt.

Bestimme jeweils einen passenden Funktionsterm, so dass die Funktion $f$ ...

... nur genau eine der drei Eigenschaften erfüllt.
... genau zwei der drei Eigenschaften erfüllt.
... alle drei Eigenschaften erfüllt.

(10 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

4 Stochastik

Die Zufallsvariable $X$ beschreibt die Auszahlung für den Spieler in Euro.

Der Erwartungswert $E(X)$ ist der erwartete Gewinn pro Spiel des Spielers.

$\color{#ffff}{x_i}$	$6$	$2$	$1$
$\color{#ffff}{P(X=x_i)}$	$\dfrac{1}{16}$	$\dfrac{3}{16}$	$\dfrac{3}{4}$

Erwartungswert $\boldsymbol{E(X)}$ berechnen

$E(X)=\dfrac{1}{16} \cdot 6+\dfrac{3}{16} \cdot 2+\dfrac{3}{4} \cdot 1=\dfrac{3}{2}$

Der Einsatz $a$ darf höchstens 1,50 Euro betragen, damit der Spieler auf lange Sicht keinen Verlust macht.

Flächeninhalt des gesamten Kreises berechnen

$\begin{array}[t]{rlll} A &=& \pi\cdot4^2 \\[5pt] &=& 16\pi \end{array}$

Flächeninhalt des roten Kreises berechnen

$\begin{array}[t]{rlll} A_{\text{rot}} &=& \pi\cdot1^2 \\[5pt] &=& \pi \end{array}$

Anteil des roten Kreises am gesamten Kreis berechnen

$\begin{array}[t]{rlll} \dfrac{A_{\text{rot}}}{A} &=& \dfrac{\pi}{16\pi} \\[5pt] &=& \dfrac{1}{16} \end{array}$

Flächeninhalt des blauen Kreisrings berechnen

$\begin{array}[t]{rlll} A_{\text{blau}} &=& \pi\cdot2^2-\pi\\[5pt] &=& 3\pi \end{array}$

Anteil des blauen Kreisrings am gesamten Kreis berechnen

$\begin{array}[t]{rlll} \dfrac{A_{\text{blau}}}{A} &=& \dfrac{3\pi}{16\pi} \\[5pt] &=& \dfrac{3}{16} \end{array}$

Flächeninhalt des grünen Kreisrings berechnen

$\begin{array}[t]{rlll} A_{\text{grün}} &=& \pi\cdot4^2-4\pi\\[5pt] &=& 12\pi \end{array}$

Anteil des grünen Kreisrings am gesamten Kreis berechnen

$\begin{array}[t]{rlll} \dfrac{A_{\text{grün}}}{A} &=& \dfrac{12\pi}{16\pi} \\[5pt] &=& \dfrac{3}{4} \end{array}$

Somit stimmt der Anteil der jeweiligen Farbe mit deren Wahrscheinlichkeit überein.

4 Lineare Algebra

Der Punkt $B$ liegt auf der Geraden $g,$ denn sein Ortsvektor ist der Stützvektor der Geraden.

Vektor $\boldsymbol{\overrightarrow{AB}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{AB} &=& \overrightarrow{OB}-\overrightarrow{OA} \\[5pt] &=& \pmatrix{3\\0\\-1}-\pmatrix{4\\2\\-3} \\[5pt] &=& \pmatrix{-1\\-2\\2} \end{array}$

Damit $\left| \overrightarrow{AB} \right|$ dem Abstand von $OA$ zu $g$ entspricht, müssen $\overrightarrow{AB}$ und der Richtungsvektor von $g$ zueinander orthogonal verlaufen.

$\begin{array}[t]{rlll} \pmatrix{-1\\-2\\2} \circ \pmatrix{-2\\4\\3} &=& (-1)\cdot(-2)+(-2)\cdot4+2\cdot3 \\[5pt] &=&2-8+6 \\[5pt] &=& 0 \end{array}$

Somit ist $\overrightarrow{AB}$ senkrecht zu $g$ und damit entspricht $|\overrightarrow{AB}|$ dem Abstand von $A$ zu $g.$

Ein möglicher Punkt ist der Spiegelpunkt von $A$ an $B.$

$\begin{array}[t]{rlll} \overrightarrow{OC} &=& \overrightarrow{OB}+\overrightarrow{AB} \\[5pt] &=& \pmatrix{3\\0\\-1}+\pmatrix{-1\\-2\\2} \\[5pt] &=& \pmatrix{2\\-2\\1} \end{array}$

Damit ist ein möglicher Punkt mit demselben Abstand der Punkt $C(2 \mid -2 \mid 1).$

5 Stochastik

Die Wahrscheinlichkeit ein Karo zu ziehen beträgt $\frac{8}{32}.$

Die Wahrscheinlichkeit eine Dame zu ziehen beträgt $\frac{4}{32}.$

Da das Ereignis nur das Ziehen von entweder Karo oder einer Dame beschreibt, muss der Fall, dass eine Karo Dame gezogen wird von der Wahrscheinlichkeit abgezogen werden. Die Wahrscheinlichkeit für das Ziehen einer Karo Dame beträgt $\frac{1}{32}.$

Somit beträgt die Wahrscheinlichkeit für das Ereignis:

$p=\dfrac{8}{32}+\dfrac{4}{32}-\dfrac{1}{32}=\dfrac{11}{32}$

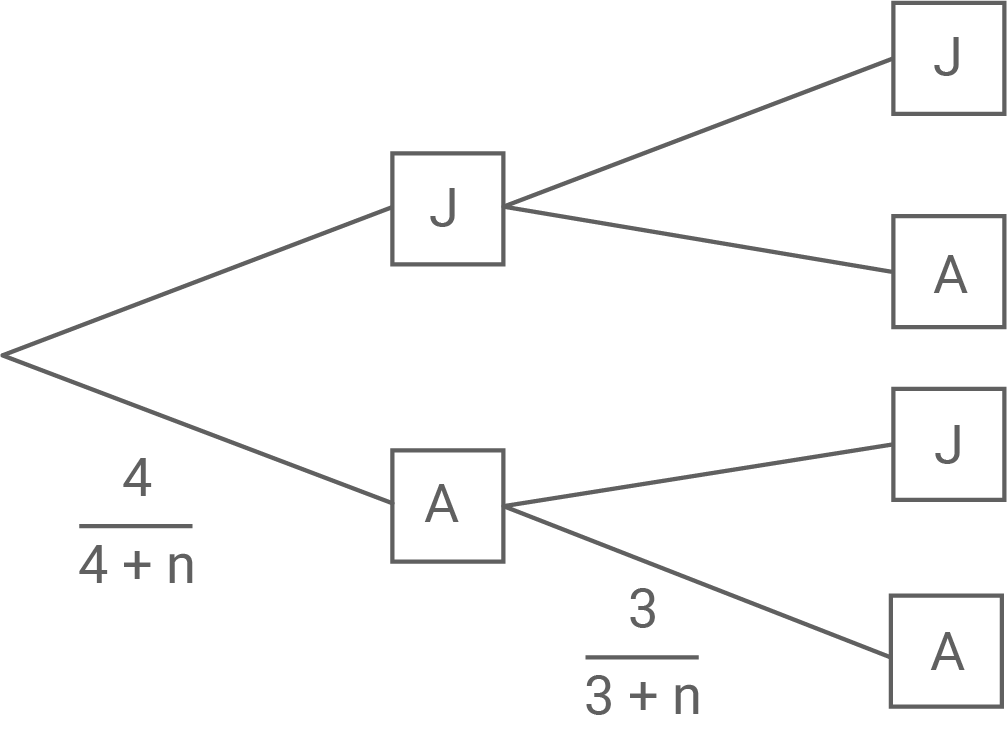
Wahrscheinlichkeitsbaum mit zwei Stufen, Knoten J und A, Wahrscheinlichkeiten 4/(4+n) und 3/(3+n), Endknoten J/A

Hilfsskizze

$A:$

„Es wird ein Ass gezogen.“

$J:$

„Es wird ein Joker gezogen.“

Die Wahrscheinlichkeit des Ereignisses zwei Asse zu ziehen beträgt $P(A,A) =\frac{2}{5}.$ Diese Wahrscheinlichkeit kann auch abstrakt als $P(A,A) = \frac{4}{4+n}\cdot\frac{3}{3+n}$ geschrieben werden (s. Hilfsskizze).
Durch Gleichsetzen folgt:

$\begin{array}[t]{rlll} \dfrac{4}{4+n}\cdot\dfrac{3}{3+n} &=& \dfrac{2}{5}\\[5pt] \dfrac{12}{n^2+7n+12} &=& \dfrac{2}{5} &\mid\; \cdot n^2+7n+12 \\[5pt] 12 &=& \dfrac{2n^2+14n+24}{5} &\mid\; \cdot 5 \\[5pt] 60 &=& 2n^2+14n+24 \end{array}$

5 Lineare Algebra

Multiplizieren der ersten Gleichung mit $5$ und anschließend von Gleichung zwei abziehen liefert:

Rechenweg anzeigen

$y =18-3z$

Sobald $x,y$ und $z$ einen Wert größer als $12$ annehmen, ist die erste Gleichung nicht erfüllt. Systematisches Einsetzen der natürlichen Zahlen für $z$ in aufsteigender Reihenfolge liefert somit direkt, dass $z\leq2$ nicht möglich ist. Werte ab $z=3$ liefern passende Ergebnisse, bis hin zu $z=6,$ danach wird $y$ negativ. Damit ergibt sich folgende Lösungsmenge von passenden Triplen $(x;y;z):$

$L=\{(0;9;3), (2;6;4), (4;3;5), (6;0;6)\}$

6 Analysis

Für eine Funktion, die genau eine der drei Eigenschaften erfüllt, kann z.B. eine nicht- $y$ -achsensymmetrische Polynomfunktion benutzt werden, die auch keinen Höhepunkt besitzt.
Für eine Funktion, die genau zwei der drei Eigenschaften erfüllt, kann z.B. eine $y$ -achsensymmetrische Polynomfunktion benutzt werden, die aber keinen Höhepunkt besitzt.
Durch Miteinbeziehung eines Hochpunkts werden dann alle drei Eigenschaften erfüllt.

Tabelle anzeigen

Anzahl erfüllter Eigenschaften	Funktionsterm	Erläuterung
$1$	$f(x)=x^3$	Polynomfunktion vom Grad 3 $f$ besitzt ungerade Exponenten, d.h. ist nicht symmetrisch zur $y$ -Achse Der Graph von $f(x)$ hat keinen Extrempunkt, nur einen Sattelpunkt bei $x=0$
$2$	$f(x)=-x^2$	Polynomfunktion vom Grad 2 $f$ besitzt nur gerade Exponenten, d.h. ist symmetrisch zur $y$ -Achse Scheitelpunkt der Parabel ist ein Tiefpunkt
$3$	$f(x)=\mathrm -x^2$	Polynomfunktion vom Grad 2 $f$ besitzt nur gerade Exponenten, d.h. ist symmetrisch zur $y$ -Achse Scheitelpunkt der Parabel ist ein Hochpunkt

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?