Vektorgeometrie 1
3
Für ein Viereck  mit den Eckpunkten
mit den Eckpunkten 

 und
und  gilt:
gilt:



3.1
Bestimme den Vektor 
Weise nach, dass dieses Viereck ein Rechteck ist.
Weise nach, dass dieses Viereck ein Rechteck ist.
3
3.2
Berechne die Koordinaten des Punktes  sodass sich die Diagonalen des Vierecks
sodass sich die Diagonalen des Vierecks  in
in  schneiden.
schneiden.
2
3.3
Durch Streckung des Vierecks  wird dessen Flächeninhalt um den Faktor
wird dessen Flächeninhalt um den Faktor  vergrößert. Die Seitenverhältnisse bleiben dabei unverändert.
Berechne eine Seitenlänge des entstehenden, vergrößerten Vierecks.
vergrößert. Die Seitenverhältnisse bleiben dabei unverändert.
Berechne eine Seitenlänge des entstehenden, vergrößerten Vierecks.
2
7
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
Vektor bestimmen



 Rechteck nachweisen
Es gilt
Rechteck nachweisen
Es gilt  und
und  Die jeweils gegenüberliegenden Seiten des Vierecks
Die jeweils gegenüberliegenden Seiten des Vierecks  sind also parallel und gleich lang.
Die Rechtwinkligkeit wird mit dem Skalarprodukt zweier benachbarter Vektoren überprüft:
sind also parallel und gleich lang.
Die Rechtwinkligkeit wird mit dem Skalarprodukt zweier benachbarter Vektoren überprüft:

 Die Vektoren
Die Vektoren  und
und  stehen also senkrecht zueinander. Also besitzt das Viereck
stehen also senkrecht zueinander. Also besitzt das Viereck  im Punkt
im Punkt  einen rechten Winkel.
einen rechten Winkel.
Wegen der Parallelität der gegenüberliegenden Seiten gilt dies für alle vier Innenwinkel. Es handelt sich also um ein Rechteck.
Wegen der Parallelität der gegenüberliegenden Seiten gilt dies für alle vier Innenwinkel. Es handelt sich also um ein Rechteck.
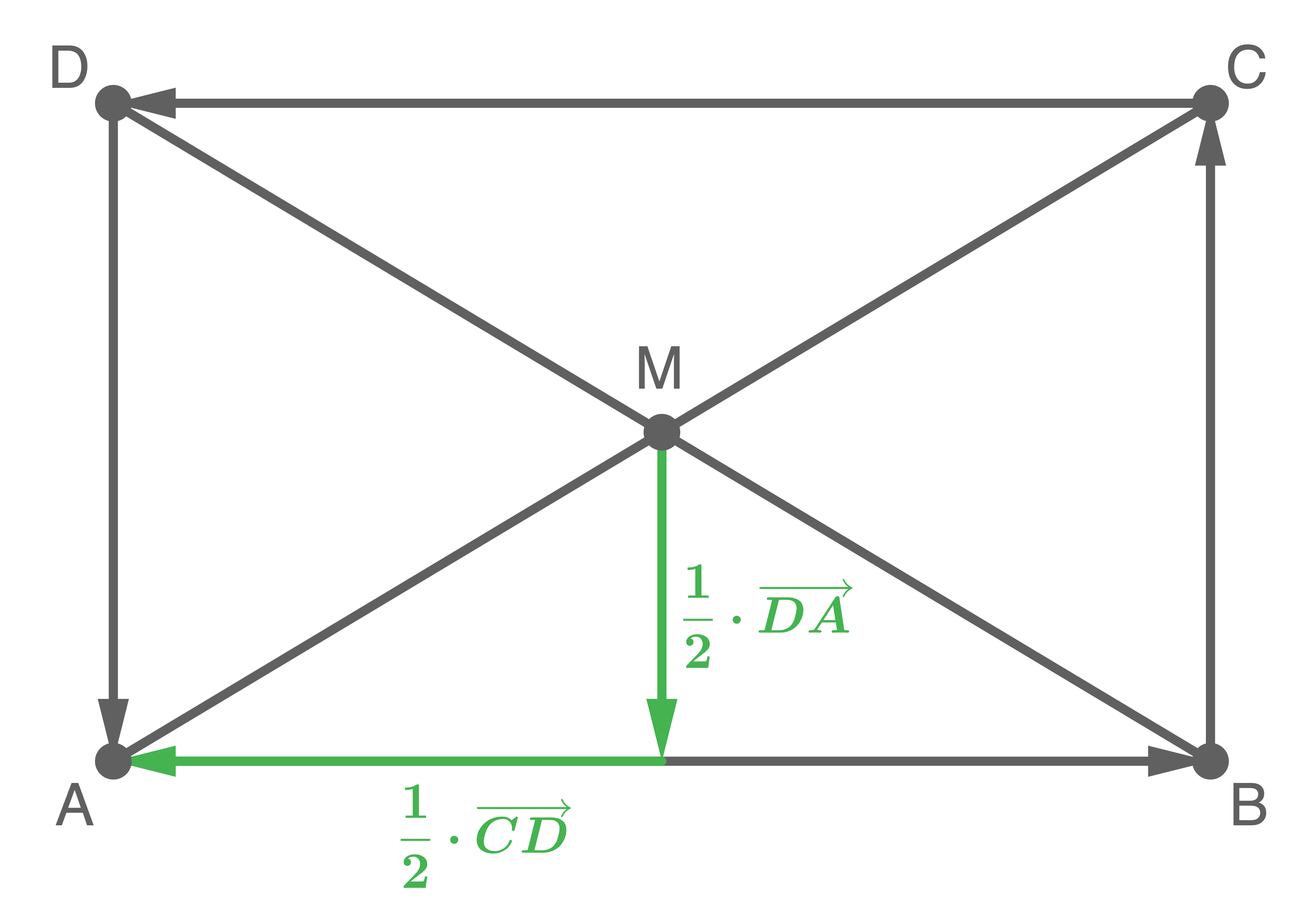
3.2
3.3
Für das Viereck  gilt:
gilt:


 Für den Flächeninhalt des gestreckten Vierecks
Für den Flächeninhalt des gestreckten Vierecks  soll gelten:
soll gelten:

 Gleichzeitig gilt:
Gleichzeitig gilt:
 also ist
also ist
 Da das Seitenverhältnis erhalten bleiben soll, gilt:
Da das Seitenverhältnis erhalten bleiben soll, gilt:
 also:
also:
 Diese Gleichung lässt sich nach
Diese Gleichung lässt sich nach  umformen:
umformen:
 Das kann in
Das kann in  eingesetzt werden:
eingesetzt werden:
![\(\begin{array}[t]{rll}
\left|\overrightarrow{A](https://mathjax.schullv.de/a83cf221aba3600f7de979086e485cfe101ee409743eb0bf819a9d897537e00b?color=5a5a5a) Eine Seite des gestreckten Vierecks ist also
Eine Seite des gestreckten Vierecks ist also  lang.
lang.