Anwendungsorientierte Analysis 2
3
Ein Fadenpendel besteht aus einem Faden, an dessen unterem Ende eine Kugel befestigt ist.
Das Pendel wird in Position P1 gebracht und zum Zeitpunkt 
losgelassen. Anschließend führt es eine Schwingung aus.
Die Geschwindigkeit der Kugel wird modelliert durch 
mit
; 
Dabei ist 
die Zeit in Sekunden 
und 
wird in Meter pro Sekunde 
angegeben.
3.1
Bestimme die Zeit, die vom Zeitpunkt des Loslassens an vergeht, bis die Kugel zum ersten Mal den Umkehrpunkt P2 erreicht.
2
3.2
Die Beschleunigung der Kugel ist die Änderungsrate der Geschwindigkeit.
Bestimme die momentane Beschleunigung der Kugel 0,2 Sekunden nach dem Loslassen sowie die durchschnittliche Beschleunigung innerhalb der ersten 0,2 Sekunden.
3
3.3
Die Funktion 
mit
; 
modelliert die Auslenkung des Pendels, wobei 
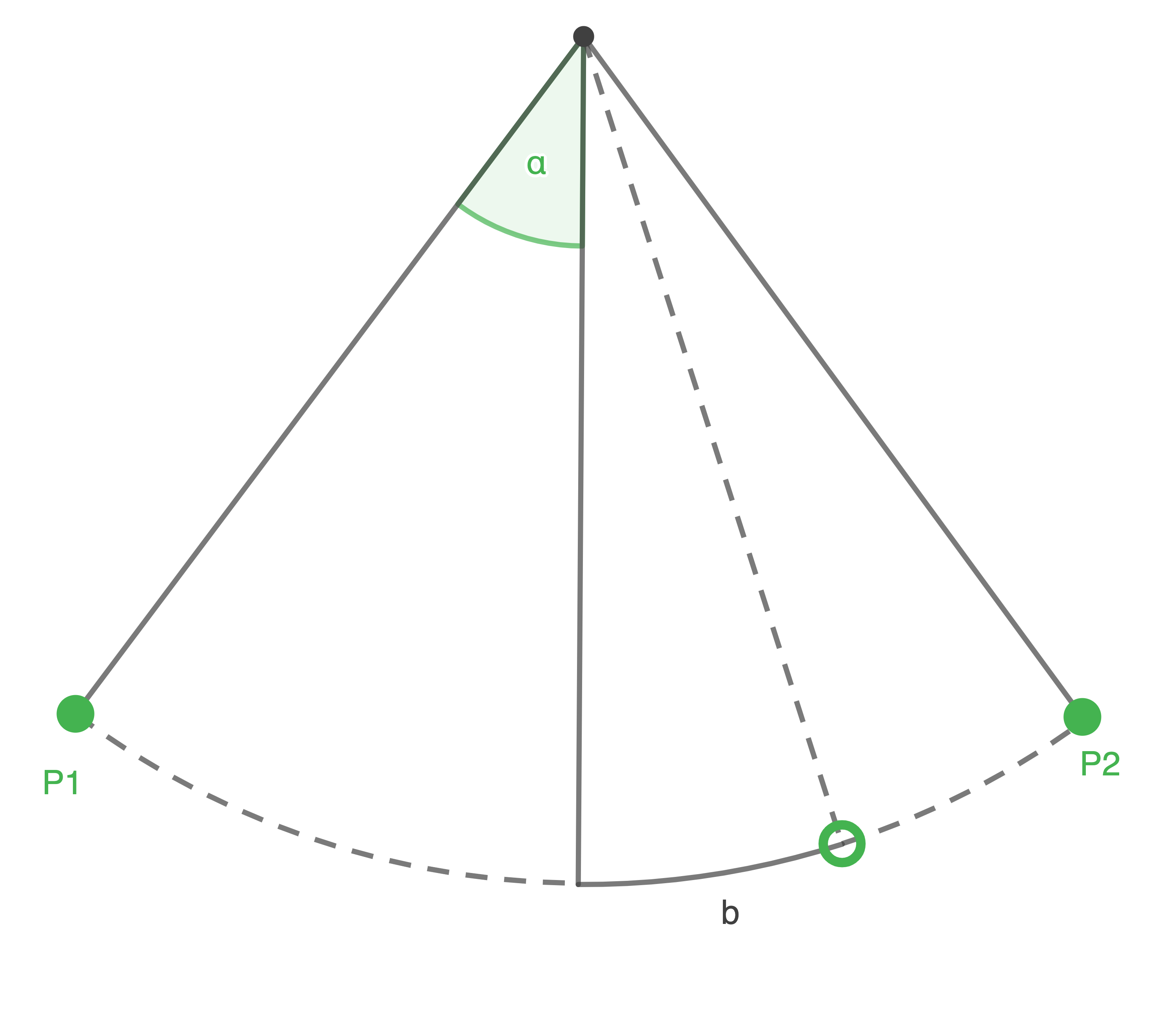
die "Länge" des Bogens vom tiefsten Punkt bis zur Position der Kugel zum Zeitpunt ist (siehe Abbildung).
Negative Werte von bedeuten dabei Auslenkungen nach links (in Richtung von P1), positive Werte bedeuten Auslenkungen nach rechts.
Negative Werte von
3.3.1
Zeige, wie man ausgehend von auf die Funktion gelangt.
3
3.3.2
Die Länge des Fadenpendels ist 
Berechne den Auslenkungswinkel
zum Zeitpunkt des Loslassens (siehe Abbildung).
Berechne den Auslenkungswinkel
2
10
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
Bis zum Umkehrpunkt P2 durchläuft die Kugel eine halbe Periode. Es gilt:
![\(\begin{array}[t]{rll}
5t&=& \pi&\quad \scriptsize \mid\;:5 \\[5pt]
t&=&\dfrac{\pi}{5}
\end{array}\)](https://mathjax.schullv.de/113ed483bcb96d6e6429042a4d8511e97bd1d3266933cefd03174ee215a4cced?color=5a5a5a)
Nach ca. 0,63 Sekunden erreicht das Pendel zum ersten Mal den Umkehrpunkt P2.
3.2
3.3.1
Da die Geschwindigkeit des Pendels und die „Länge“ des Bogens, also sozusagen die Strecke beschreibt, ist die Funktion eine Stammfunktion von 
Eine Stammfunktion von 
ist 
Damit folgt:
Damit folgt:
3.3.2
Zum Zeitpunkt gilt 
Der Bogen von P1 bis zum tiefsten Punkt hat also eine Länge von 
Mit der Formel für die Bogenlänge gilt: