Anwendungsorientierte Analysis 3
4
Die Mantelfläche einer ein Meter hohen Vase wird durch Rotation des Schaubilds der Funktion 
mit 
um die 
-Achse modelliert. Dabei entspricht eine Längeneinheit einem Dezimeter 
in der Realität. Die Dicke des Vasenbodens und die Wandstärke der Vase werden vernachlässigt.
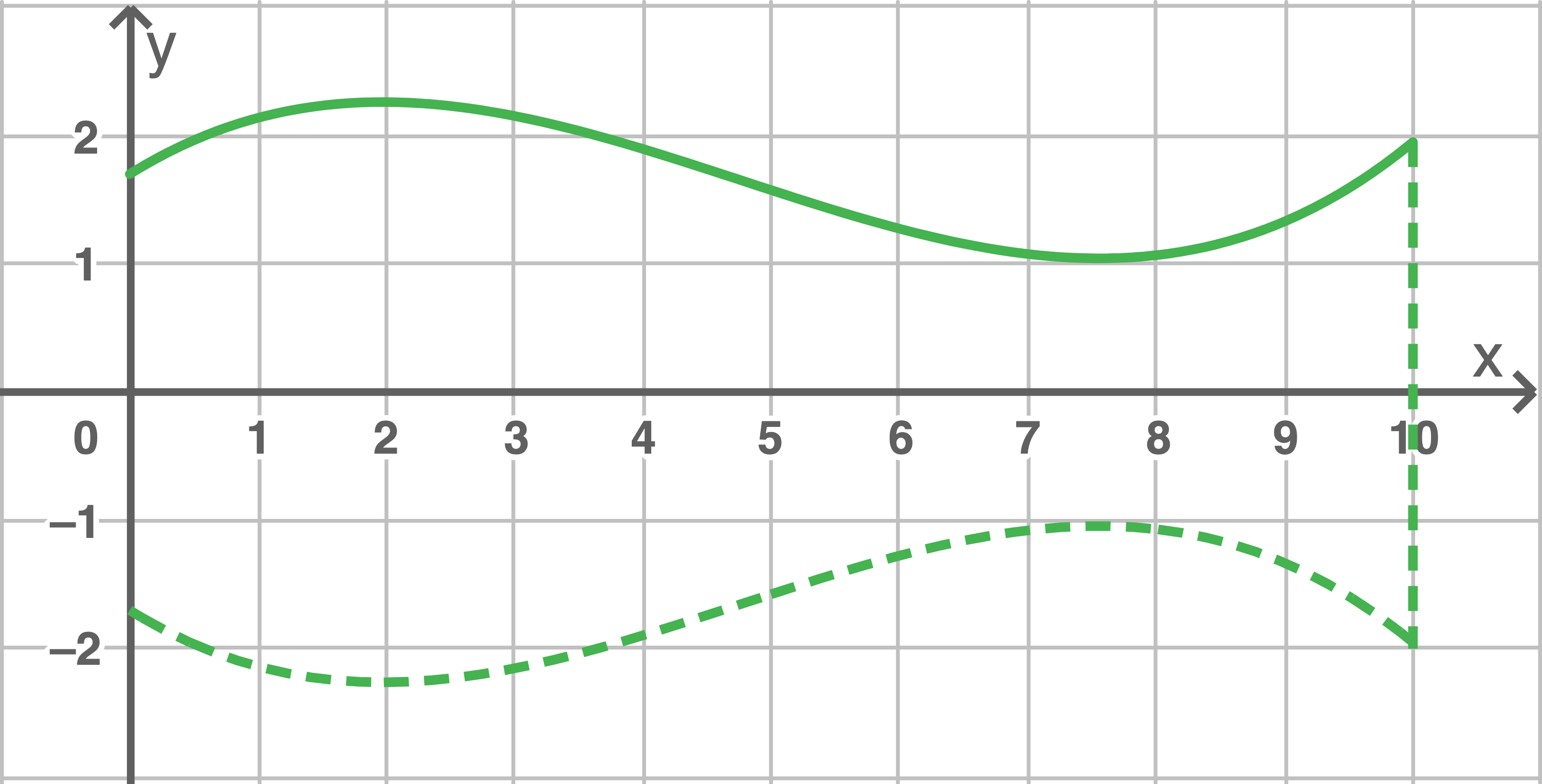
Abbildung 1: Modellierung der Vasenkontur mit 
Das Schaubild von ist als durchgezogene Kurve dargestellt.
Abbildung 2: Vase
4.1
Bestimme den Wert des Flächeninhalts des Bodens der Vase.
Berechne die Differenz aus dem Durchmesser der Vasenöffnung und dem Durchmesser des Vasenbodens.
2
4.2
Beurteile, ob die folgende Aussage wahr oder falsch ist:
„Der größte Durchmesser der Vase ist größer als
“
„Der größte Durchmesser der Vase ist größer als
3
4.3
Es gilt: 
Das Design der Vase soll nun geändert werden. Bis zu einer Höhe von 
soll dabei das Modell beibehalten werden. Ab dieser Höhe wird eine Gerade verwendet, die sich knickfrei an das Schaubild von anschließt.
Bestimme die Höhe der derart veränderten Vase, falls deren Fassungsvermögen insgesamt
Liter betragen soll.
Bestimme die Höhe der derart veränderten Vase, falls deren Fassungsvermögen insgesamt
5
10
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
4.1
Wert des Flächeninhalts des Bodens bestimmen
Der Boden der Vase ist kreisförmig. Der Radius 
in 
entspricht 
![\(r= f(0)= 0,014\cdot 0^3-0,2\cdot 0^2+0,625\cdot 0+1,7 = 1,7\,\text{[dm]}\)](https://mathjax.schullv.de/dfe0c57d447e7937ea2bad6c085b9bf08e6b2757f7dc6496c312367f5a310091?color=5a5a5a)
Für den Flächeninhalt des Bodens ergibt sich somit:
Der Wert des Flächeninhalts des Vasenbodens beträgt ca. 
Differenz der Durchmesser berechnen
Durchmesser Vasenöffnung:
![\(= 3,9\,\text{[dm]}\)](https://mathjax.schullv.de/74c3dedc5ba78d6879405da32879c364d6cb8435d62e817d9b6d692e7f9fd1ad?color=5a5a5a)
Durchmesser Vasenboden:
Der Durchmesser der Vasenöffnung ist 
größer als der Durchmesser des Vasenbodens.
4.2
Damit der größte Durchmesser größer als 
ist, muss der größte Radius größer als 
sein.
Der Radius der Vase wird durch beschrieben. Es wird also der größte Funktionswert von zwischen 
und 
gesucht.
1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f(x) &=& 0,014\cdot x^3-0,2\cdot x^2+0,625\cdot x +1,7\\[5pt]
f](https://mathjax.schullv.de/2f71a44cee994958fbd5f6399f7d0056f0408f4dd622dadb83753ad54eb25463?color=5a5a5a)
Gleichsetzen von 
liefert mögliche Extremstellen von 
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/2a948ec53b7b3f36edb63dc834ca88e6131dc13be1cc7a86a345d5489b046434?color=5a5a5a)
2. Schritt: Funktionswerte vergleichen
Der größte Funktionswert von wird entweder in einer der beiden Stellen 
oder 
oder in einem der Intervallränder angenommen.
![\(\begin{array}[t]{rll}
f\left(0\right) &=& 1,7 \\[5pt]
f\left(\dfrac{200-25\sqrt{22}}{42}\right) &=& 0,014\cdot \left(\dfrac{200-25\sqrt{22}}{42}\right)^3-0,2\cdot \left(\dfrac{200-25\sqrt{22}}{42}\right)^2\\[5pt]
&&+0,625\cdot \left(\dfrac{200-25\sqrt{22}}{42}\right) + 1,7 \\[5pt]
&\approx& 2,26
\end{array}\)](https://mathjax.schullv.de/1ccbb969ce19b6e273f1e2ff33798c54a6ac6131c13f9debea13940830242526?color=5a5a5a)
Die übrigen Funktionswerte müssen nicht berechnet werden, da sich hieraus bereits schließen lässt, dass es mindestens eine Stelle gibt, an der der Radius der Vase größer als und somit auch der Durchmesser der Vase größer als ist.
Die Aussage ist also wahr.
Der Radius der Vase wird durch
Die Aussage ist also wahr.
4.3
1. Schritt: Geradengleichung bestimmen
Die Geradengleichung hat die Form 
Da die Gerade knickfrei an das Schaubild von anschließen soll, beträgt ihre Steigung:
Zudem muss sie durch den Punkt 
verlaufen.
Einsetzen in die Geradengleichung:
![\(\begin{array}[t]{rll}
g(5) &=& 1,575 \\[5pt]
m\cdot 5 +b &=& 1,575 &\quad \scriptsize \mid\; m = -0,325\\[5pt]
-0,325\cdot 5 +b &=& 1,575 \\[5pt]
-1,625 + b &=& 1,575 &\quad \scriptsize \mid\; + 1,625\\[5pt]
b &=& 3,2
\end{array}\)](https://mathjax.schullv.de/637bd56d6fa2df7a967d96372aacd15088a97138d08aeb6a25f250d4b1241c30?color=5a5a5a)
Die Gerade lässt sich also durch 
beschreiben.
2. Schritt: Höhe bestimmen
Wegen 
beträgt das Volumen des Vasenteils, der mit Hilfe des Schaubildes von beschrieben wir, ca. 
Der Teil der Vase, der mit Hilfe der Geraden
modelliert wird, muss also noch ein Volumen von ca. 
besitzen.
Für die Höhe 
der Vase muss daher folgendes gelten:
![\(\begin{array}[t]{rll}
\pi\cdot\displaystyle\int_{5}^{h}(g(x))^2\;\mathrm dx &\approx& 4,43 \\[5pt]
\pi\cdot\displaystyle\int_{5}^{h}(-0,325x +3,2)^2\;\mathrm dx &\approx& 4,43 \\[5pt]
\pi\cdot\displaystyle\int_{5}^{h}\left(\frac{169}{1600}x^2- \frac{52}{25}x+ \frac{256}{25}\right)\;\mathrm dx &\approx& 4,43 \\[5pt]
\pi\cdot\left[\frac{169}{4800}x^3- \frac{26}{25}x^2+ \frac{256}{25}x\right]_5^{h} &\approx& 4,43 \\[5pt]
\pi\cdot\left(\frac{169}{4800}h^3- \frac{26}{25}h^2+ \frac{256}{25}h - \left(\frac{169}{4800}\cdot 5^3- \frac{26}{25}\cdot 5^2+ \frac{256}{25}\cdot 5\right)\right) &\approx& 4,43 \\[5pt]
\pi\cdot\left(\frac{169}{4800}h^3- \frac{26}{25}h^2+ \frac{256}{25}h - \frac{28.417}{960}\right) &\approx& 4,43 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/299f397f376f54b7c7c2b66eaab846227626c224c5b4fc7bcf6b4f1913df9d81?color=5a5a5a)
Mit dem WTR lässt sich die Gleichung lösen zu:
Die Höhe der geänderten Vase beträgt ca. 
Da die Gerade knickfrei an das Schaubild von
Der Teil der Vase, der mit Hilfe der Geraden