Analysis
1.1
Die Funktion 
ist gegeben durch 
; 
.
Das Schaubild von ist 
.
Die erste Ableitung von
von ist 
; und die zweite Ableitung 
von ist 
; .
Das Schaubild von
Die erste Ableitung von
1.1.1
Weise nach, dass 
der Hochpunkt von ist.
Gib eine Gleichung der Asymptote von an.
Gib eine Gleichung der Asymptote von
4
1.1.2
Zeichne für 
.
3
1.1.3
Zeige, dass 
mit 
; eine Stammfunktion von ist.
Bestimme den Wert von
in der Gleichung: 
.
Bestimme den Wert von
5
1.2
Für 
sind die Funktionen 
mit 
und 
mit 
gegeben.
Die Abbildung zeigt die Schaubilder
von und 
von .
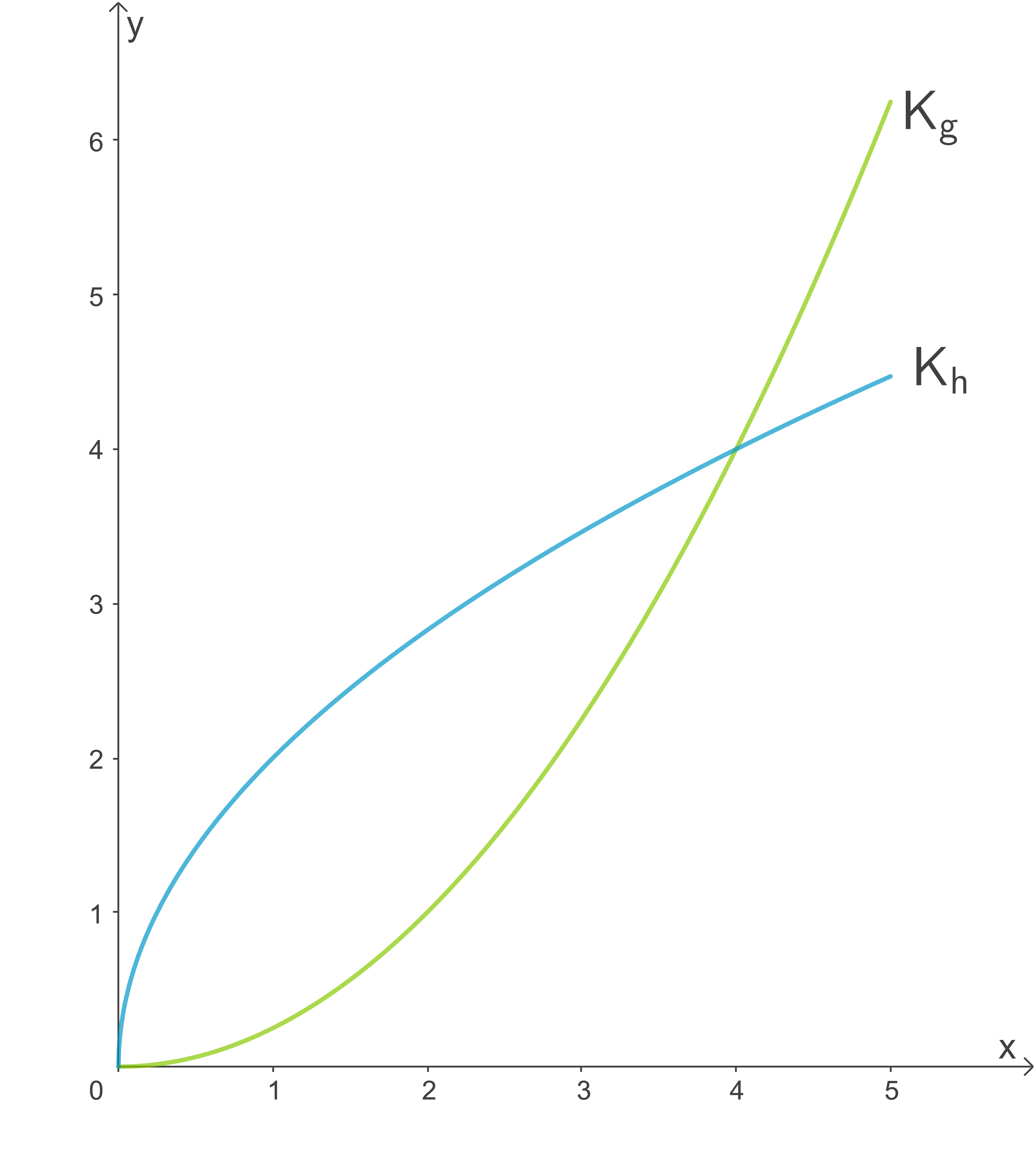
Die Abbildung zeigt die Schaubilder
1.2.1
Prüfe folgende Aussage:
"Die Gerade durch die beiden Punkte
und 
ist sowohl die Normale von in 
als auch die Normale von in 
."
"Die Gerade durch die beiden Punkte
4
1.2.2
Die 
-Achse, und die Parallele zur 
-Achse mit der Gleichung 
, mit 
, begrenzen eine Fläche. Durch Rotation dieser Fläche um die -Achse entsteht ein Rotationskörper.
Bestimme den Wert von
, sodass dessen Volumen 
beträgt.
Bestimme den Wert von
4
1.1.1
Hochpunkt:
Notweniges Kriterium für Extremstellen: 
Hinreichendes Kriterium für Extremstellen: 
Der Punkt mit den Koordinaten 
ist ein Hochpunkt von .
Asymptote:
Untersuche das Verhalten für 
Für 
, gilt: 
Für
, gilt: 
besitzt für eine waagerechte Asymptote mit der Gleichung 
.
Für
1.1.2
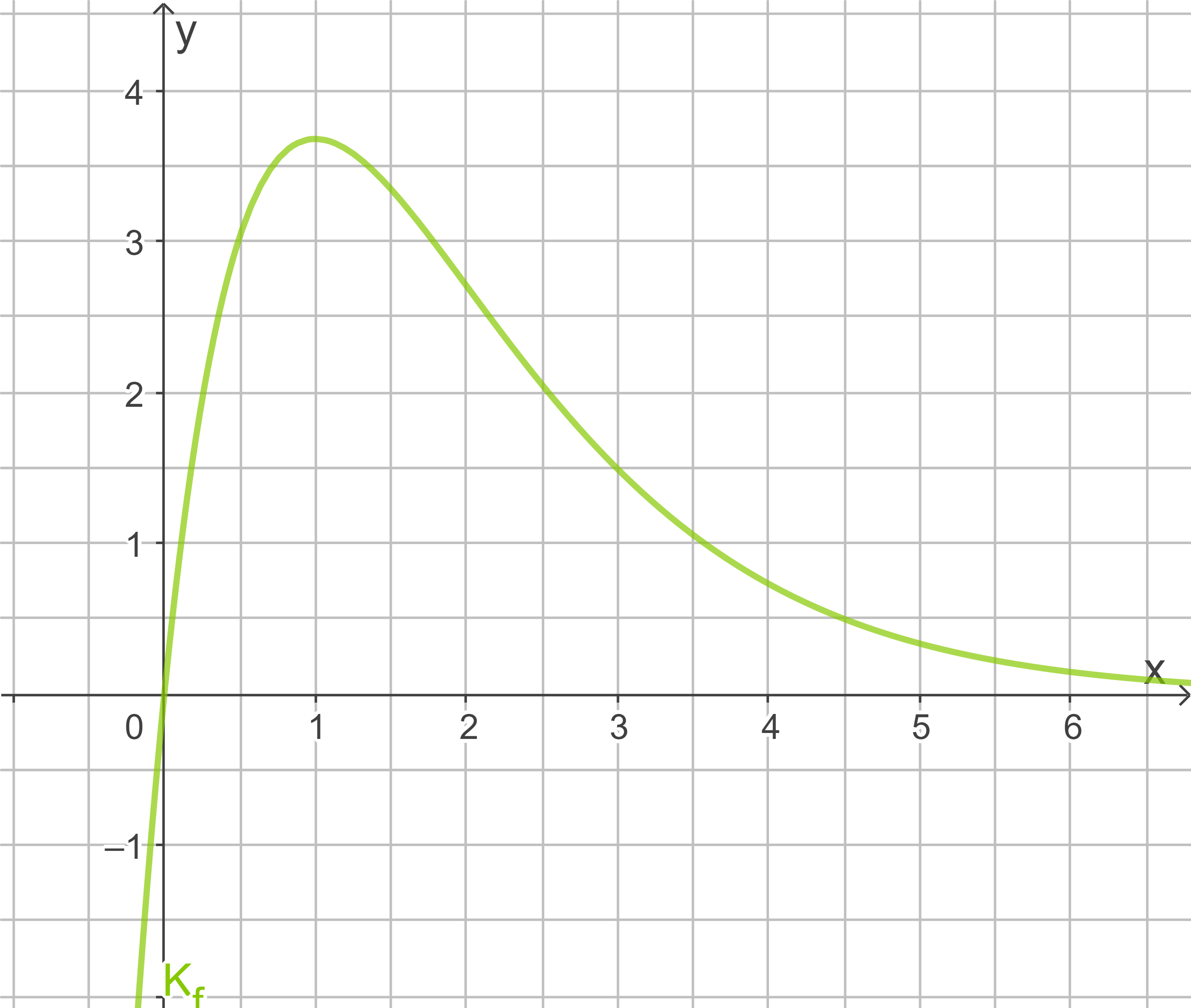
1.1.3
Für eine Stammfunktion gilt: 
![\(\begin{array}[t]{rll}
F(x)&=&-10\,\mathrm{e}^{-x} \cdot (x+1) \\[5pt]
F](https://mathjax.schullv.de/ccbf6067f3ae1977a5f0d3a0c23494fb2f864c1acfc136a8625668ceaf74970a?color=5a5a5a)
ist eine Stammfunktion von , da gilt.
![\(\begin{array}[t]{rll}
\displaystyle\int_{1}^{2}f(x) \mathrm dx&=&\left[F(x)\right]^{2}_{1} \\[5pt]
&=&\left[-10 \cdot (x+1) \cdot \mathrm{e}^{-x}\right]^{2}_{1} \\[5pt]
&=&-10 \cdot (2+1) \cdot \mathrm{e}^{-2}-(-10) \cdot 2 \cdot \mathrm{e}^{-1} \\[5pt]
&=&-30 \cdot \mathrm{e}^{-2}+20 \cdot \mathrm{e}^{-1}
\end{array}\)](https://mathjax.schullv.de/5968aec2d9c61dc9e9ce0bf64cf3db420d05c193928e909ab318e2b0ffbedac2?color=5a5a5a)
![\(\begin{array}[t]{rll}
-30 \cdot \mathrm{e}^{-2}+20 \cdot \mathrm{e}^{-1}&=&\dfrac{a \cdot \mathrm{e}-30}{\mathrm{e}^2} &\quad \scriptsize \mid\; \cdot \mathrm{e}^2 \\[5pt]
-30+20 \cdot \mathrm{e}&=&a \cdot \mathrm{e}-30 &\quad \scriptsize \mid\;+30 \\[5pt]
20 \cdot \mathrm{e}&=&a \cdot \mathrm{e} &\quad \scriptsize \mid\;:\mathrm{e}\\[5pt]
20&=&a
\end{array}\)](https://mathjax.schullv.de/51276f43adae21be1714334a4c41aaa23c1b20053606d5faed5307dff0770343?color=5a5a5a)
1.2.1
Normale von in 
:
Punktprobe mit :
![\(\begin{array}[t]{rll}
y&=&-1 \cdot x+c \\[5pt]
2&=&-1+c &\quad \scriptsize \mid\;+1 \\[5pt]
3&=&c
\end{array}\)](https://mathjax.schullv.de/df329e125b96a1446acc6aa6434354f87890c578abea30ce04d70c41c6dc1025?color=5a5a5a)
Normale von in 
:
Punktprobe mit :
![\(\begin{array}[t]{rll}
y&=&-1 \cdot x+c \\[5pt]
1&=&-1 \cdot 2\cdot+c &\quad \scriptsize \mid\;+2 \\[5pt]
3&=&c
\end{array}\)](https://mathjax.schullv.de/3f10c44b4914cc31ee3c7970c63ad808eb3453db27fd4912659e41f12dc60803?color=5a5a5a)
Die Aussage ist wahr, da die Gerade und die Normalen 
und 
die gleiche Funktionsgleichung 
beitzen.
1.2.2
Obere Integrationsgrenze:
![\(\begin{array}[t]{rll}
c&=&h(x) \\[5pt]
c&=&2\sqrt{x} &\quad \scriptsize \mid\;:2\\[5pt]
\dfrac{c}{2}&=&\sqrt{x} &\quad \scriptsize \mid\;^2\\[5pt]
\dfrac{1}{4}c^2&=&x
\end{array}\)](https://mathjax.schullv.de/ef0a7ba8c5254889f6cf668162e7c45d5b94cb437caa1c68db0cab9e251c8467?color=5a5a5a)
![\(\begin{array}[t]{rll}
\pi \cdot \displaystyle\int_{0}^{\frac{1}{4}c^2}c^2 \mathrm dx &=&\pi \cdot \left[c^2 \cdot x\right]^{\frac{1}{4}c^2}_{0} \\[5pt]
&=&\pi \cdot (c^2 \cdot \dfrac{1}{4}c^2-0) \\[5pt]
&=&\dfrac{\pi}{4} \cdot c^4
\end{array}\)](https://mathjax.schullv.de/3a8c4252e26ef5bceec7fed32da72d4e5d275470c4be8303940129d8fda683eb?color=5a5a5a)
![\(\begin{array}[t]{rll}
\pi \cdot \displaystyle\int_{0}^{\frac{1}{4}c^2}h(x)^2 \mathrm dx&=&\pi \cdot \displaystyle\int_{0}^{\frac{1}{4}c^2}(2\sqrt{x})^2 \mathrm dx \\[5pt]
&=&\pi \cdot \displaystyle\int_{0}^{\frac{1}{4}c^2}4x\, \mathrm dx \\[5pt]
&=&\pi \cdot \left[2x^2\right]^{\frac{1}{4}c^2}_{0} \\[5pt]
&=&\pi \cdot \left(2\left(\dfrac{1}{4}c^2\right)^2-0\right) \\[5pt]
&=&\dfrac{\pi}{8} \cdot c^4
\end{array}\)](https://mathjax.schullv.de/4c16245b4c580e6f2dc0ff6880237f86301bd6c882cdbe2835db541483296944?color=5a5a5a)
![\(\begin{array}[t]{rll}
32\pi&=&\dfrac{\pi}{4} \cdot c^4-\dfrac{\pi}{8} \cdot c^4 \\[5pt]
32\pi&=&\dfrac{\pi}{8} \cdot c^4 &\quad \scriptsize \mid\;:\dfrac{\pi}{8} \\[5pt]
256&=&c^4 &\quad \scriptsize \mid\;4\sqrt{\,} \\[5pt]
4&=&c_1 \\[5pt]
(-4&=&c_2)
\end{array}\)](https://mathjax.schullv.de/202c56dde92113862a2111809b3382ef12ec466938994dcb2694a615d2ee3f4f?color=5a5a5a)
Für 
beträgt das Volumen des Rotationskörpers 
.