Pflichtaufgaben
1 Analysis
Gegeben ist die in
a)
Bestimme die Koordinaten und die Art der Extrempunkte von  .
.
(3 BE)
b)
Begründe, dass  die
die  -Achse im Intervall
-Achse im Intervall ![\([-2; 0]\)](https://www.schullv.de/resources/formulas/92ab3567249ec777800012e9fd2e4c83236aabd94f0ededb3c37cefa2b974bb9_light.svg) schneidet.
schneidet.
(2 BE)
2 Stochastik
Eine große Sportartikelmarke untersucht ihre Beliebtheit in verschiedenen Altersgruppen. Von den Befragten unter 20 Jahren gaben 40 % an, Fans der Marke zu sein. Unter den Befragten, die mindestens 20 Jahre alt waren, waren 65 % Fans der Marke. Insgesamt waren 30 % der Befragten unter 20 Jahre alt.
a)
Stelle die Situation in einem vollständig beschrifteten Baumdiagramm dar.
(3 BE)
b)
Gib eine Frage im gegebenen Sachzusammenhang an, die mit Hilfe des Terms
 beantwortet werden kann.
beantwortet werden kann.
(2 BE)
3 Lineare Algebra
Gegeben sind die Punkte
a)
Weise folgende Sachverhalte nach:
(1)
Der Punkt  ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke 
(2)
Die Vektoren  und
und  schließen einen rechten Winkel ein.
schließen einen rechten Winkel ein.
(2 BE)
b)
Bestimme die Koordinaten eines Punktes, der doppelt so weit vom Punkt  entfernt ist wie vom Punkt
entfernt ist wie vom Punkt 
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?1 Analysis
a)
b)
2 Stochastik
a)
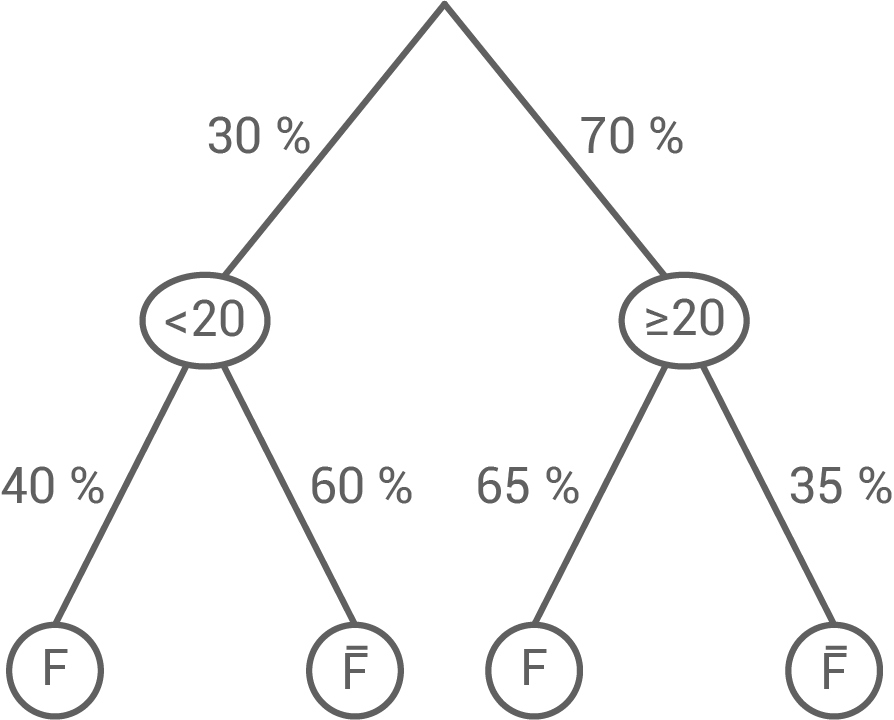
b)
Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person mindestens 20 Jahre alt ist, wenn sie ein Fan der Marke ist?
3 Lineare Algebra
a)
(1)
(2)
Damit stehen die beiden Vektoren senkrecht aufeinander und schließen einen rechten Winkel ein.
b)