Vektorgeometrie 2

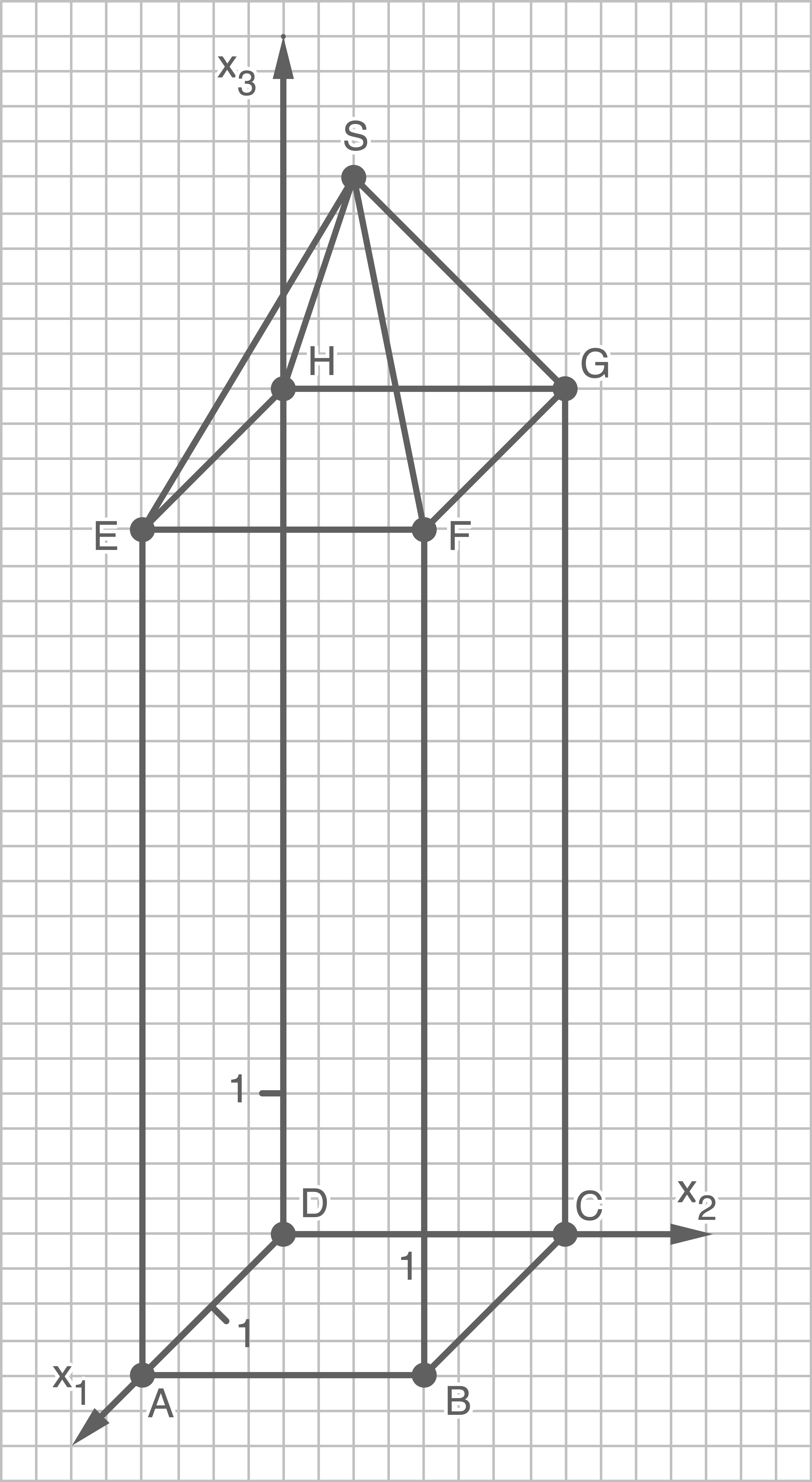
Betrachtet wird das Modell einer Kirche. Der Kirchturm besteht aus einem Quader mit aufgesetzter Pyramide.

Einer Bauzeichnung kann man Folgendes entnehmen: Die Punkte $A(2\mid0\mid0),$ $B(2\mid2\mid0),$ $C(0\mid2\mid0)$ und $D(0\mid0\mid0)$ bilden die Grundfläche. Das Dach hat die vier Eckpunkte $E(2\mid0\mid6),$ $F(2\mid2\mid6),$ $G(0\mid2\mid6),$ $H(0\mid0\mid6)$ und die Turmspitze $S(1\mid1\mid8).$

Eine Längeneinheit entspricht $10$ Meter $(\text{m}).$

2.1

Zeichne das Modell des Kirchturms in ein geeignetes Koordinatensystem.

2.2

Das Dach des Kirchturms soll vollständig gedeckt werden. Hierfür werden Ziegel verwendet, die pro Ziegel $0,12\,\text{m}^2$ abdecken. Die Ziegel werden auf Paletten mit jeweils $200$ Ziegeln geliefert.

Bestimme die kleinstmögliche Anzahl von Paletten, die geliefert werden müssten.

2.3

Der Vektor $\pmatrix{1\\2\\-4}$ modelliert zu einem bestimmten Zeitpunkt die Richtung des einfallenden Sonnenlichtes.

2.3.1

Berechne den Winkel, unter dem das Sonnenlicht auf den Boden (d.h. $x_1x_2$ -Ebene) trifft.

2.3.2

Auf der Turmspitze $S$ befindet sich ein senkrecht stehendes Kreuz der Höhe $h.$ Der Kirchturm und das Kreuz werfen einen Schatten. Der Schattenpunkt des höchsten Punktes ist $P(3,1\mid5,2\mid0).$ Bestimme die Höhe $h.$

2.4

Im Kirchturm soll eine Glocke eingebaut werden. Die Position der Glocke wird im Modell mit $Q$ bezeichnet. Der Abstand von $Q$ zu den Eckpunkten $E,$ $F,$ $G$ und $H$ des Daches soll jeweils dreimal so groß sein wie der Abstand von $Q$ zur Turmspitze $S.$

Ermittle die Koordinaten des Punktes $Q.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Modell eines Kirchturms - BaWü Abi berufl. Gymnasium 2022

2.2

Den Koordinaten von $E,$ $F,$ $G$ und $H$ lässt sich entnehmen, dass die Grundfläche des Dachs parallel zur $x_1x_2$ -Ebene liegt und die Form eines Quadrats hat.
Den Koordinaten von $S$ lässt sich zudem entnehmen, dass $S$ genau über dem Mittelpunkt der Dachgrundfläche liegt und die Pyramide daher gerade ist.

Da es sich also um eine gerade Pyramide mit quadratischer Grundfläche handelt, sind alle vier Seitenflächen gleich groß.
Mit der Formel für den Flächeninhalt eines Dreiecks ergibt sich:

Rechenweg anzeigen

$A_{EFS} =\sqrt{5}\,\text{[FE]}$

$1\,\text{FE}$ ist $10\,\text{m}\cdot 10\,\text{m} = 100\,\text{m}^2$ groß. Insgesamt muss also folgender Flächeninhalt mit den Ziegeln bedeckt werden:

$A_{Dach} = 4\cdot\sqrt{5}\,\text{FE}$ $= 4\cdot\sqrt{5}\cdot 100\,\text{m}^2$ $= 400\cdot\sqrt{5}\,\text{m}^2$

Für die Anzahl der benötigten Ziegel folgt:

$400\cdot\sqrt{5}\,\text{m}^2 : 0,12\,\text{m}^2$ $\approx 7.454$

Es werden also ca. $7.454$ Ziegel benötigt.

Auf jeder Palette befinden sich 200 Ziegel:

$7.454 :200 = 37,27$

Es müssten also mindestens 38 Paletten geliefert werden.

2.3.1

Die Sonnenstrahlen können als Geraden mit dem Richtungsvektor $\pmatrix{1\\2\\-4}$ modelliert werden.
Ein Normalenvektor der $x_1x_2$ -Ebene ist $\pmatrix{0\\0\\1}.$

Mit der Formel für den Schnittwinkel $\alpha$ zwischen einer Geraden und einer Ebene folgt:

Rechenweg anzeigen

$\alpha \approx 60,79^{\circ}$

Das Sonnenlicht trifft in einem Winkel von ca. $60,79^{\circ}$ auf den Boden.

2.3.2

Da das Kreuz senkrecht auf der Kirchturmspitze steht, liegt der höchste Punkt auf der Geraden durch den Punkt $S$ mit dem Richtungsvektor $\pmatrix{0\\0\\1}.$

$h: \, \overrightarrow{x} = \pmatrix{1\\1\\8} + t\cdot \pmatrix{0\\0\\1},$ $t\in \mathbb{R}$

Zudem befindet sich der höchste Punkt auch auf einer gemeinsamen Gerade mit seinem Schattenpunkt $P,$ die entlang der Richtung der Sonnenstrahlen verläuft:

$s:\, \overrightarrow{x} = \pmatrix{3,1\\5,2\\0} + u\cdot \pmatrix{1\\2\\-4},$ $u\in\mathbb{R}$

Der höchste Punkt $\(P$ ist also der Schnittpunkt dieser beiden Geraden.
Gleichsetzen:

Rechenweg anzeigen

$\pmatrix{2,1\\4,2\\-8} = t\cdot \pmatrix{0\\0\\1} - u\cdot \pmatrix{1\\2\\-4}$

Daraus ergibt sich folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& 2,1 &=& -u \\ \text{II}\quad& 4,2 &=& -2u \\ \text{III}\quad& -8 &=& t+4u \\ \end{array}$

Aus $\text{I}$ und $\text{II}$ folgt direkt $u= -2,1.$ Für $t$ folgt damit aus $\text{III}:$

$\begin{array}[t]{rll} -8 &=& t+ 4\cdot (-2,1) \\[5pt] -8 &=& t -8,4 \quad \scriptsize \mid\; +8,4\\[5pt] 0,4 &=& t \end{array}$

Jetzt kann beispielsweise $t$ in die Geradengleichung von $h$ eingesetzt werden:

$\(\overrightarrow{OP$

Der höchste Punkt hat also die Koordinaten $\(P$ und befindet sich demnach auf einer Höhe von $8,4\,\text{LE}.$
Die Kirchturmspitze befindet sich in einer Höhe von $8\,\text{LE}.$
Für die Höhe des Kreuzes folgt:

$h=8,4\,\text{LE}-8\,\text{LE} = 0,4\,\text{LE} = 4\,\text{m}$

2.4

Da $Q$ zu den vier Eckpunkten $E,$ $F,$ $G$ und $H$ den gleichen Abstand haben soll, besitzt $Q$ die gleichen $x_1$ - und $x_2$ -Koordinaten wie $S.$

$Q$ hat in Abhängigkeit von $t$ also die Koordinaten $Q_t(1\mid 1\mid t)$ mit $t\in \mathbb{R}$ und $6\leq t\leq 8$ damit $Q$ innerhalb des Daches liegt.

Der Abstand von $Q_t$ zu $E$ (und damit auch den übrigen Eckpunkten der Dachgrundfläche) soll dreimal so groß sein, wie der Abstand von $Q_t$ zu $S.$

Rechenweg anzeigen

$\begin{array}[t]{rll} t_1 &=& 8,25 + \sqrt{0,8125} \\[5pt] &\approx& 9,15 \\[5pt] t_2 &=& 8,25 - \sqrt{0,8125} \\[5pt] &\approx& 7,35 \\[5pt] \end{array}$

Da die Glocke für $t\gt 8$ oberhalb des Daches liegen würde, kommt nur $t_2$ infrage. Die Koordinaten lauten also:

$Q(1\mid 1\mid 8,25 - \sqrt{0,8125})$ bzw. gerundet $Q(1\mid 1\mid 7,35)$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?