Vektorgeometrie 2
3
Die Gerade 
geht durch die Punkte 
und 
3.1
Begründe, dass parallel zur 
Koordinatenebene ist, aber nicht in dieser Ebene liegt.
2
3.2
Bestimme einen Punkt 
auf 
sodass 2:1 das Verhältnis der Streckenlängen 
ist.
2
3.3
Weise nach, dass die Vektoren
Berechne den Abstand von
3
7
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
Da 
und 
die gleiche 
-Koordinate 
haben, gilt dies auch für alle anderen Punkte auf 
Für alle Punkte in der
-Koordinatenebene gilt allerdings 
Somit liegt zwar parallel zu aber nicht in dieser Ebene.
Für alle Punkte in der
3.2
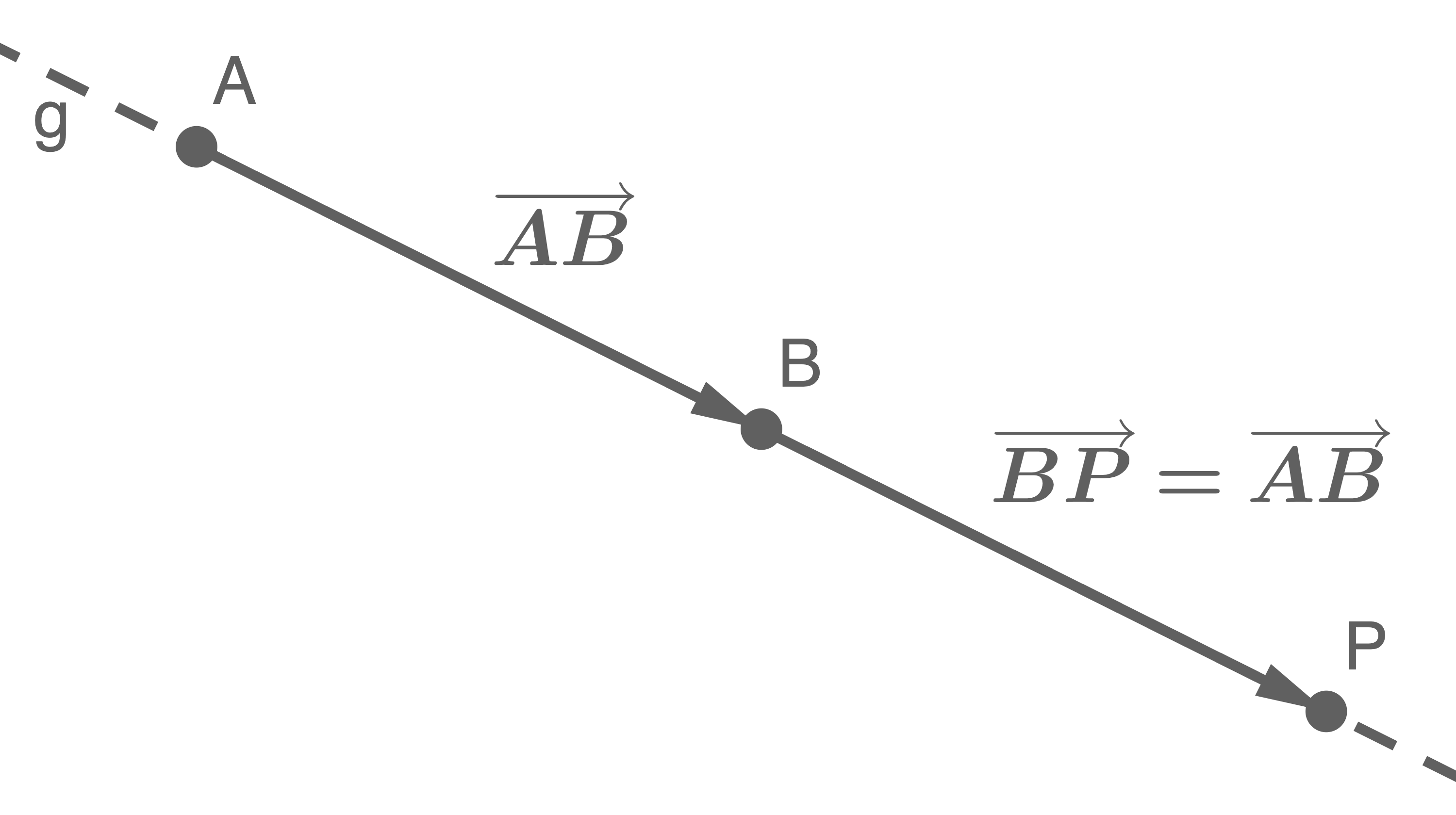
Der Punkt muss doppelt so weit von entfernt sein, wie von und soll auf der Geraden liegen.
Eine Möglichkeit für ist daher:
![\(\begin{array}[t]{rll}
\overrightarrow{OP} &=& \overrightarrow{OA} + 2\cdot \overrightarrow{AB} \\[5pt]
&=& \pmatrix{2\\-2\\2} + 2\cdot \pmatrix{2-2\\ 4-(-2) \\ 5-2 } \\[5pt]
&=& \pmatrix{2\\10\\8}
\end{array}\)](https://mathjax.schullv.de/6935b423b97a6077ee22202817ac1883a5b37d3396a7683ac998757f12df569e?color=5a5a5a)
Mögliche Koordinaten sind also 
Eine Möglichkeit für
3.3
Orthogonalität nachweisen
Zwei Vektoren sind orthogonal, wenn ihr Skalarprodukt Null ergibt:
![\(\begin{array}[t]{rll}
\overrightarrow{AB}\circ \overrightarrow{MC} &=& \pmatrix{2-2 \\ 4-(-2) \\ 5-2}\circ \pmatrix{4-2\\2-1\\1,5-3,5} \\[5pt]
&=& \pmatrix{0 \\ 6 \\ 3}\circ \pmatrix{2\\1\\-2}\\[5pt]
&=& 0\cdot 2 +6\cdot 1 + 3\cdot (-2) \\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/7834438cb03f3fd75d7c563da9d4aeb3b16923172366535da6e70fc13f8e98d2?color=5a5a5a)
Die beiden Vektoren 
und 
sind also orthogonal zueinander.
Abstand berechnen
Da orthogonal zur ist, liegt auch orthogonal zur Geraden Zudem liegt 
auf Für den Abstand von 
zu gilt daher:
![\(\begin{array}[t]{rll}
d(C,g) &=& \left|\overrightarrow{MC} \right| \\[5pt]
&=& \left| \pmatrix{2\\1\\-2} \right| \\[5pt]
&=& \sqrt{2^2 +1^2 + (-2)^2} \\[5pt]
&=& 3
\end{array}\)](https://mathjax.schullv.de/8bc3b00129bdf73d5a1d262f413b601e7abb41bbf87f65775b363066da95e68b?color=5a5a5a)
Der Abstand von zur Geraden beträgt drei Längeneinheiten.