Lineare Algebra

Aufgabe I 3

Gegeben sind die Gerade $g: \overrightarrow{x}=\pmatrix{-1\\-2\\5}+r \cdot\pmatrix{1\\0\\1}, r \in \mathbb{R}$ und die Punkte $A(5\mid-1\mid 4),$ $B(1\mid1\mid 0)$ und $C(0\mid3\mid 2).$

Bestimme die Koordinaten der Schnittpunkte von $g$ mit den Koordinatenebenen.

(3 BE)

$h$ ist die Gerade durch $A$ und $B.$
Zeige, dass $g$ und $h$ zueinander windschief sind.

(4 BE)

Gib eine Gleichung einer Ebene an, die parallel zur $x_1 x_3$ -Ebene ist und von $C$ den Abstand $2$ hat.

(2 BE)

Es gilt: $\overrightarrow{AB} \cdot \overrightarrow{BC}=0.$

Erläutere, welche geometrische Größe durch den Term

$\dfrac{1}{2}\cdot\left| \overrightarrow{AB} \right| \cdot\left| \overrightarrow{BC} \right|$

berechnet wird.

(2 BE)

Es gibt genau einen Kreis, auf dem die Punkte $A, B$ und $C$ liegen.
Zeige, dass der Mittelpunkt dieses Kreises auf der Hypotenuse des Dreiecks $ABC$ liegt.

(4 BE)

Aufgabe II 3

Die Form eines Schirms für eine Stehlampe wird durch die Punkte $A(0\mid0\mid 0), B(4 \mid0 \mid 0), C(4 \mid4 \mid 0),$ $D(0\mid4 \mid 0), E(1 \mid1 \mid 8),$ $F(3 \mid1 \mid 8), G(3 \mid3 \mid 8)$ und $H(1 \mid3 \mid 8)$ beschrieben. Eine Längeneinheit entspricht $10\; \text{cm}.$

Zeichne den Lampenschirm in ein Koordinatensystem ein.

(3 BE)

Zeige, dass die Seitenfläche $ADHE$ ein Trapez ist.

(2 BE)

Beurteile die folgende Aussage:
Die Kante $BF$ schließt mit der $x_1x_2$ -Ebene einen Winkel von mehr als $81^{\circ}$ ein.

(3 BE)

Zur Stabilisierung sollen im Inneren des Lampenschirms dünne Stäbe angebracht werden.
Formuliere in dieser Anwendungssituation eine Aufgabenstellung, die sich mit folgendem Ansatz lösen lässt:

$\pmatrix{4\\0\\0}+s \cdot\pmatrix{-3\\3\\8}=\pmatrix{4\\4\\0}+t \cdot\pmatrix{-3\\-3\\8} ;$ $s, t \in[0 ; 1]$

(3 BE)

Im Lampenschirm soll eine LED-Lampe installiert werden. Diese soll von allen Eckpunkten den gleichen Abstand haben. Die LED-Lampe wird vereinfacht als punktförmig angenommen.
Bestimme die Koordinaten dieses Punktes.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Aufgabe I 3

Da der Richtungsvektor von $g$ keine $x_2$ -Koordinate besitzt, verläuft $g$ parallel zur $x_1x_3$ -Ebene. Somit gibt es keinen Schnittpunkt mit der $x_1x_3$ Ebene

Schnittpunkt mit der $\boldsymbol{x_1x_2}$ -Ebene bestimmen

Damit $g$ die $x_1x_2$ -Ebene schneidet, muss die $x_3$ -Koordinate gleich $0$ sein.
Dies ist der Fall, wenn $r=-5$ ist.
Somit gilt für den Schnittpunkt:

$\begin{array}[t]{rlll} \overrightarrow{OS}_{1,2} &=& \pmatrix{-1\\-2\\5}-5\cdot\pmatrix{1\\0\\1} \\[5pt] &=& \pmatrix{-6\\-2\\0} \end{array}$

Somit folgen für die Koordinaten des Schnittpunktes $S_{1,2}(-6 \mid -2 \mid 0).$

Schnittpunkt mit der $\boldsymbol{x_2x_3}$ -Ebene bestimmen

Damit $g$ die $x_2x_3$ -Ebene schneidet, muss die $x_1$ -Koordinate gleich $0$ sein.
Dies ist der Fall, wenn $r=1$ ist.
Somit gilt für den Schnittpunkt:

$\begin{array}[t]{rlll} \overrightarrow{OS}_{2,3} &=& \pmatrix{-1\\-2\\5}+1\cdot\pmatrix{1\\0\\1} \\[5pt] &=& \pmatrix{0\\-2\\6} \end{array}$

Somit folgen für die Koordinaten des Schnittpunktes $S_{2,3}(0 \mid -2 \mid 6).$

Geradengleichung von $h$ aufstellen

$\begin{array}[t]{rlll} h:\overrightarrow{x} &=& \overrightarrow{OA}+s\cdot\overrightarrow{AB} \\[5pt] &=& \overrightarrow{OA}+s\cdot\left(\overrightarrow{OB}-\overrightarrow{OA}\right) \\[5pt] &=& \pmatrix{5\\-1\\4}+s\cdot\left(\pmatrix{1\\1\\0}-\pmatrix{5\\-1\\4}\right) \\[5pt] &=& \pmatrix{5\\-1\\4}+s\cdot\pmatrix{-4\\2\\-4} \end{array}$

Lineares Gleichungssystem aufstellen

$\begin{array}[t]{rlll} \pmatrix{-1\\-2\\5}+r\cdot\pmatrix{1\\0\\1} &=& \pmatrix{5\\-1\\4}+s\cdot\pmatrix{-4\\2\\-4} &\mid\; -\pmatrix{-1\\-2\\5}\\[5pt] r\cdot\pmatrix{1\\0\\1} &=& \pmatrix{6\\1\\-1}+ s\cdot\pmatrix{-4\\2\\-4}&\mid\; -s\cdot\pmatrix{-4\\2\\-4}\\[5pt] r\cdot\pmatrix{1\\0\\1}-s\cdot\pmatrix{-4\\2\\-4} &=& \pmatrix{6\\1\\-1} \end{array}$

Aus Zeile 2 folgt für $s:$

$\begin{array}[t]{rlll} 0r-2s &=& 1 &\mid\; :(-2) \\[5pt] s &=& -\dfrac{1}{2} \end{array}$

Aus Zeile 1 folgt für $r:$

$\begin{array}[t]{rlll} r-(-\dfrac{1}{2})\cdot(-4) &=& 6 &\mid\; +2 \\[5pt] r &=& 8 \end{array}$

Das Überprüfen des LGS mit Zeile 3 liefert:

$\begin{array}[t]{rlll} 8\cdot1-(-\dfrac{1}{2})\cdot(-4) &=& -1 &\mid\; \\[5pt] 6 &\neq& -1 \end{array}$

Nach systematischem Ausprobieren folgt, dass das LGS keine Lösung hat. Somit schneiden sich $g$ und $h$ nicht.
Zusätzlich sind die Richtungsvektoren keine Vielfachen voneinander. Somit sind $g$ und $h$ auch nicht parallel.
Damit müssen die Geraden windschief sein.

Die Ebene ist parallel zur $x_1x_3$ -Ebene. Somit werden für die Spannvektoren die klassischen Spannvektoren der $x_1x_3$ Ebene gewählt.
Nun wird der Stützvektor so gewählt, dass er einen Abstand von $2$ zum Punkt $C$ hat, z.B. $\pmatrix{0\\1\\2}.$

Eine mögliche Ebenengleichug folgt also mit:

$E:\overrightarrow{x}=\pmatrix{0\\1\\2}+r\cdot\pmatrix{1\\0\\0}+s\cdot\pmatrix{0\\0\\1}; r,s \in \mathbb{R}$

Das Dreieck $ABC$ hat bei $B$ einen rechten Winkel. Somit entspricht die Höhe des Dreiecks der Strecke $\left| \overrightarrow{BC} \right|$ und die Grundseite des Dreiecks der Strecke $\left| \overrightarrow{AB} \right|.$ Für den Term des Flächeninhalts folgt:

$A= \dfrac{1}{2}\cdot \left| \overrightarrow{AB} \right|\cdot \left| \overrightarrow{BC} \right|$

Somit gibt der Term den Flächeninhalt des Dreiecks $ABC$ an.

Die Strecke $\overline{AC}$ muss die Hypotenuse des Dreiecks $ABC$ sein, da sich im Punkt $B$ ein rechter Winkel befindet.

Auf der Hypotenuse $\overline{AC}$ hat nur ihr Mittelpunkt $M$ denselben Abstand von $A$ und $C.$

Mittelpunkt $\boldsymbol{M}$ der Hypotenuse $\boldsymbol{\overrightarrow{AC}}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{OM} &=& \overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt] &=& \overrightarrow{OA}+\dfrac{1}{2}\cdot\left(\overrightarrow{OC}-\overrightarrow{OA}\right) \\[5pt] &=& \pmatrix{5\\-1\\4}+\dfrac{1}{2}\cdot\left(\pmatrix{0\\3\\2}-\pmatrix{5\\-1\\4}\right) \\[5pt] &=& \pmatrix{2,5\\1\\3} \end{array}$

Abstand $\boldsymbol{\left| \overrightarrow{AM} \right|}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{AM} \right| &=& \sqrt{(-2,5)^2+2^2+(-1)^2}\\[5pt] &\approx& 3,35 \end{array}$

Abstand $\boldsymbol{\left| \overrightarrow{MB} \right|}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{MB} \right| &=& \sqrt{(-1,5)^2+0^2+(-3)^2}\\[5pt] &\approx& 3,35 \end{array}$

Abstand $\boldsymbol{\left| \overrightarrow{CM} \right|}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{CM} \right| &=& \sqrt{2,5^2+(-2)^2+1^2}\\[5pt] &\approx& 3,35 \end{array}$

Da alle drei Punkte denselben Abstand zum Mittelpunkt der Strecke $\overline{AC}$ haben, befinden sie sich auf einem Kreis, dessen Mittelpunkt auf der Hypotenuse des Dreiecks $ABC$ liegt.

Aufgabe II 3

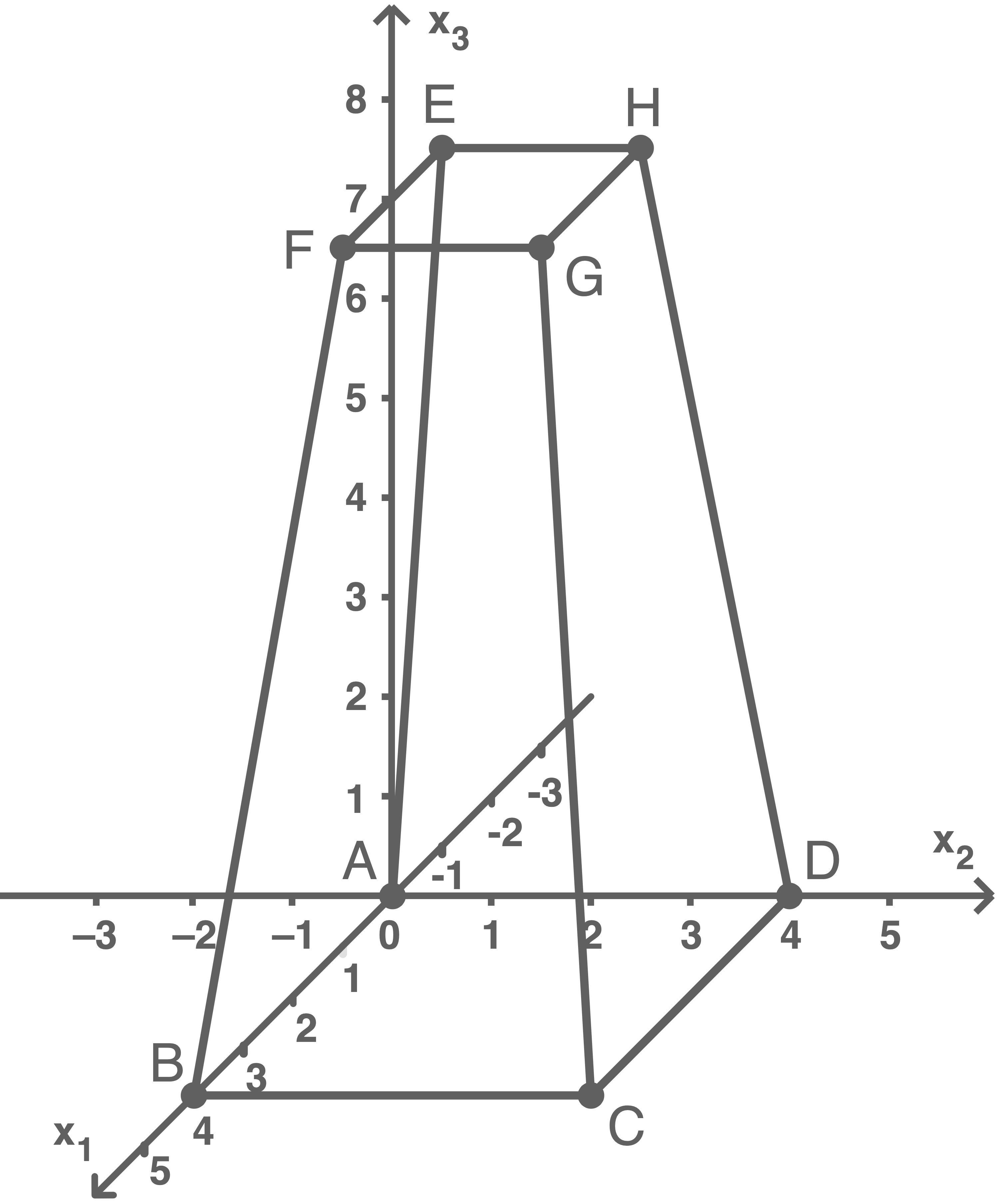
Grafik eines dreidimensionalen Koordinatensystems mit Punkten und Linien.

Damit ein Viereck ein Trapez ist, müssen zwei gegenüberliegende Kanten zueinander parallel sein.

$\boldsymbol{\overrightarrow{AD}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{AD} &=& \overrightarrow{OD}-\overrightarrow{OA} \\[5pt] &=&\pmatrix{0\\4\\0}-\pmatrix{0\\0\\0} \\[5pt] &=& \pmatrix{0\\4\\0} \end{array}$

$\boldsymbol{\overrightarrow{EH}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{EH} &=& \overrightarrow{OH}-\overrightarrow{OE} \\[5pt] &=&\pmatrix{1\\3\\8}-\pmatrix{1\\1\\8} \\[5pt] &=& \pmatrix{0\\2\\0} \end{array}$

Es gilt $\overrightarrow{AD}=\overrightarrow{EH}\cdot2.$ Somit sind die beiden Kanten parallel zueinander.
Da die Bedingung für ein Trapez erfüllt ist, ist das Viereck $ADHE$ ein Trapez.

$\boldsymbol{\overrightarrow{BF}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{BF} &=& \overrightarrow{OF}-\overrightarrow{OB} \\[5pt] &=&\pmatrix{3\\1\\8}-\pmatrix{4\\0\\0} \\[5pt] &=& \pmatrix{-1\\1\\8} \end{array}$

Eine mögliche orthogonale Projektion des Vektors $\overrightarrow{BF}$ ist $\pmatrix{-1\\1\\0}.$

Winkel zwischen $\boldsymbol{\overrightarrow{BF}}$ und der $\boldsymbol{x_1x_2}$ -Ebene berechnen

$\begin{array}[t]{rlll} \cos(\alpha) &=& \dfrac{\left| \pmatrix{-1\\1\\8}\circ\pmatrix{-1\\1\\0} \right|}{\left| \pmatrix{-1\\1\\8}\right|\cdot\left|\pmatrix{-1\\1\\0} \right|} \\[5pt] \cos(\alpha) &=& \dfrac{\left| -1\cdot (-1)+1\cdot1+8\cdot0\right|}{\sqrt{(-1)^2+1^2+8^2}\cdot\sqrt{(-1)^2+1^2+0^2}}\\[5pt] \cos(\alpha) &=& \dfrac{2}{\sqrt{66}\cdot\sqrt{2}} &\mid\; \cos^{-1} \\[5pt] \alpha &=& \cos^{-1}\left(\dfrac{2}{\sqrt{66}\cdot\sqrt{2}}\right) \\[5pt] \alpha &=& 79,98^\circ \end{array}$

Somit ist die Behauptung falsch.

Die Stäbe verbinden die Punkte $B$ und $H$ bzw. $C$ und $E.$ Es soll überprüft werden, ob sich die Stäbe kreuzen.

Der Punkt, der von den Eckpunkten des Lampenschirms den gleichen Abstand hat, liegt aus Symmetriegründen auf der Geraden durch den Punkt $(2\mid2\mid 0)$ mit Richtungsvektor $\pmatrix{0\\0\\1}.$ Die Koordinaten des gesuchten Punktes $P$ haben also die Form $P(2\mid2 \mid t)$ mit $0 \leq t \leq 4.$

Aus Symmetriegründen reicht es die Abstände $\left| \overrightarrow{AP} \right|=\left| \overrightarrow{EP} \right|$ gleichzusetzen.

$\boldsymbol{\overrightarrow{AP}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{AP} &=& \overrightarrow{OP}-\overrightarrow{OA} \\[5pt] &=& \pmatrix{2\\2\\t}-\pmatrix{0\\0\\0} \\[5pt] &=& \pmatrix{2\\2\\t} \end{array}$

$\boldsymbol{\overrightarrow{EP}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{EP} &=& \overrightarrow{OP}-\overrightarrow{OE} \\[5pt] &=& \pmatrix{2\\2\\t}-\pmatrix{1\\1\\8} \\[5pt] &=& \pmatrix{1\\1\\t-8} \end{array}$

$\boldsymbol{t}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{AP} \right| &=& \left| \overrightarrow{EP} \right| \\[5pt] \sqrt{2^2+2^2+t^2} &=& \sqrt{1^2+1^2+(t-8)^2} &\mid\; ^2 \\[5pt] 8+t^2 &=& 2+(t-8)^2 &\mid\; -2;-t^2 \\[5pt] 6+t^2 &=& (t-8)^2&\mid\; -t^2 \\[5pt] 6 &=&t^2-2\cdot8t+64-t^2 &\mid\; -64 \\[5pt] -58 &=& -16t &\mid\; :(-16)\\[5pt] \dfrac{29}{8} &=& t \end{array}$

Somit folgt, dass die LED-Lampe im Punkt $\left(2 \mid 2 \mid \frac{29}{8}\right)$ befestigt werden muss.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?