Stochastik

Aufgabe I 2

Ein Sportverein hat $800$ Mitglieder, von denen $200$ jugendlich sind. Alle anderen Mitglieder sind erwachsen. Insgesamt engagieren sich $10\, \%$ aller Mitglieder ehrenamtlich im Sportverein. $536$ Mitglieder sind erwachsen und engagieren sich nicht ehrenamtlich im Sportverein.

Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.

(3 BE)

Beurteile, ob der Anteil derjenigen, die sich ehrenamtlich im Sportverein engagieren, unter den erwachsenen Mitgliedern genauso groß ist wie unter den jugendlichen Mitgliedern.

(2 BE)

In einer Umkleidekabine treffen sich zufällig drei Mitglieder des Sportvereins.
Berechne die Wahrscheinlichkeit, dass alle drei jugendlich sind.

(2 BE)

Dem Sportverein tritt eine Gruppe Erwachsener bei, die sich aber alle nicht ehrenamtlich engagieren.
Dadurch steigt bei den nicht ehrenamtlich engagierten Mitgliedern der Anteil der Erwachsenen auf über $75\, \%.$
Ermittle, wie viele Personen mindestens beigetreten sind.

(4 BE)

Zur Jahreshauptversammlung des Sportvereins kommen insgesamt $75$ Mitglieder. Es wird angenommen, dass die Anzahl der Teilnehmer, die für eine Beitragserhöhung stimmen werden, binomialverteilt ist mit $p=0,6.$

Berechne die Wahrscheinlichkeit für folgende Ereignisse:

$A:$

„Mindestens $41$ Mitglieder stimmen für eine Beitragserhöhung.“

$B:$

„Es stimmen mehr als $35$ und höchstens $39$ Mitglieder für eine Beitragserhöhung.“

(4 BE)

Aufgabe II 2

Ein Restaurant verkauft industriell hergestellte Frühlingsrollen. Eine Untersuchung hat gezeigt, dass $17\, \%$ der industriell hergestellten Frühlingsrollen das vorgegebene Gewicht unterschreiten.

Es werden drei Frühlingsrollen bestellt. Dabei soll untersucht werden, wie viele Frühlingsrollen das vorgegebene Gewicht unterschreiten.

Stelle den Sachverhalt durch ein geeignetes beschriftetes Baumdiagramm dar.
Berechne die Wahrscheinlichkeit, dass mindestens zwei der drei Frühlingsrollen das vorgegebene Gewicht unterschreiten.

(5 BE)

Die Wahrscheinlichkeit eines Ereignisses $A$ lässt sich wie folgt berechnen:

$P(A)=1-0,83^{20}$

Beschreibe in der Anwendungssituation ein passendes Zufallsexperiment sowie ein mögliches Ereignis $A.$

(2 BE)

Die Verbraucherzentrale kontrolliert stichprobenartig das Gewicht der Frühlingsrollen. Dazu werden in einer Stichprobe $1500$ Frühlingsrollen untersucht. Es erfolgt eine Beanstandung, wenn die in der Stichprobe ermittelte Anzahl der zu leichten Frühlingsrollen um mehr als eine Standardabweichung nach oben vom Erwartungswert dieser Anzahl abweicht.

Bestimme die Wahrscheinlichkeit für eine Beanstandung.

(4 BE)

Ermittle die Anzahl an Frühlingsrollen, die man mindestens kaufen muss, damit man mit einer Wahrscheinlichkeit von mindestens $99\, \%$ mindestens $20$ Frühlingsrollen erhält, die das vorgegebene Gewicht einhalten.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Aufgabe I 2

	Jugendliche	Erwachsene	Summe
Ehrenamt	$16$	$64$	$80$
kein Ehrenamt	$184$	$536$	$720$
Summe	$200$	$600$	$800$

Der Anteil der im Sportverein ehrenamtlich engagierten erwachsenen Mitglieder beträgt $\frac{64}{600}.$

Der Anteil der im Sportverein ehrenamtlich engagierten jugendlichen Mitgliedern beträgt $\frac{16}{200}$ oder erweitert $\frac{48}{600}.$

Da $\frac{48}{600}\lt\frac{64}{600}$ gilt, stimmt die Aussage nicht, denn der Anteil derjenigen die sich ehrenamtlich engagieren, ist unter den erwachsenen Mitgliedern größer.

Von allen $800$ Mitgliedern sind $200$ jugendliche Mitglieder. Somit beträgt die Wahrscheinlichkeit einen einzelnen Jugendlichen in der Umkleidekabine zu treffen $\frac{200}{800}.$

Jetzt ist bereits ein Jugendlicher, und somit auch ein Mitglied des Sportvereins, in der Umkleide. Die Wahrscheinlichkeit, dass sich noch ein zweiter Jugendlicher in der Umkleide aufhält beträgt also $\frac{199}{799}.$

Mit dem dritten Jugendlichen verhält es sich genau so. Die Wahrscheinlichkeit, dass er in der Umkleide ist beträgt $\frac{198}{798}.$

Somit beträgt die Wahrscheinlichkeit, dass sich zufällig drei jugendliche Mitglieder in der Umkleide treffen $\frac{200}{800}\cdot\frac{199}{799}\cdot\frac{198}{798}\approx0,0154,$ also $15,4\,\%.$

$k$ ist die Anzahl der neuen Erwachsenen, die sich nicht ehrenamtlich engagieren.

Durch die neue Gruppe steigt bei den nicht ehrenamtlich engagierten Mitgliedern der Anteil der Erwachsenen auf über $75 \, \%.$ Somit folgt folgende Gleichung:

$\begin{array}[t]{rlll} \dfrac{536+k}{720+k}&\gt&0,75 &\mid\; \cdot (720+k) \\[5pt] 536+k &\gt& 540+0,75k &\mid\; - 536 \\[5pt] k &\gt& 4+0,75k &\mid\;-0,75k \\[5pt] 0,25k &\gt& 4&\mid\; \cdot 4 \\[5pt] k &\gt& 16 \end{array}$

Somit sind mindestens $17$ Personen beigetreten.

$X$ beschreibt die Anzahl derjenigen, die eine Beitragserhöhung befürworten und ist binomialverteilt mit $n=75$ und $p=0,6.$

Wahrscheinlichkeit $\boldsymbol{P(A)}$ berechnen

$\begin{array}[t]{rlll} P(A) &=& P(X \geq 31) \\[5pt] &=& 1-P(X \leq 40) \\[5pt] &\approx& 1-0,145 \\[5pt] &=& 0,855 \\[5pt] &=& 85,5 \,\% \end{array}$

Wahrscheinlichkeit $\boldsymbol{P(B)}$ berechnen

$\begin{array}[t]{rlll} P(B) &=& P(35\lt X \leq 39) \\[5pt] &=& P(X \leq 39)-P(X \leq 35) \\[5pt] &\approx& 0,0981-0,0133 \\[5pt] &=& 0,0848 \\[5pt] &=& 84,8 \, \% \end{array}$

Aufgabe II 2

$G:$

„Das vorgeschriebene Gewicht wird eingehalten.“

$\overline{G}:$

„Das vorgeschriebene Gewicht wird nicht eingehalten.“

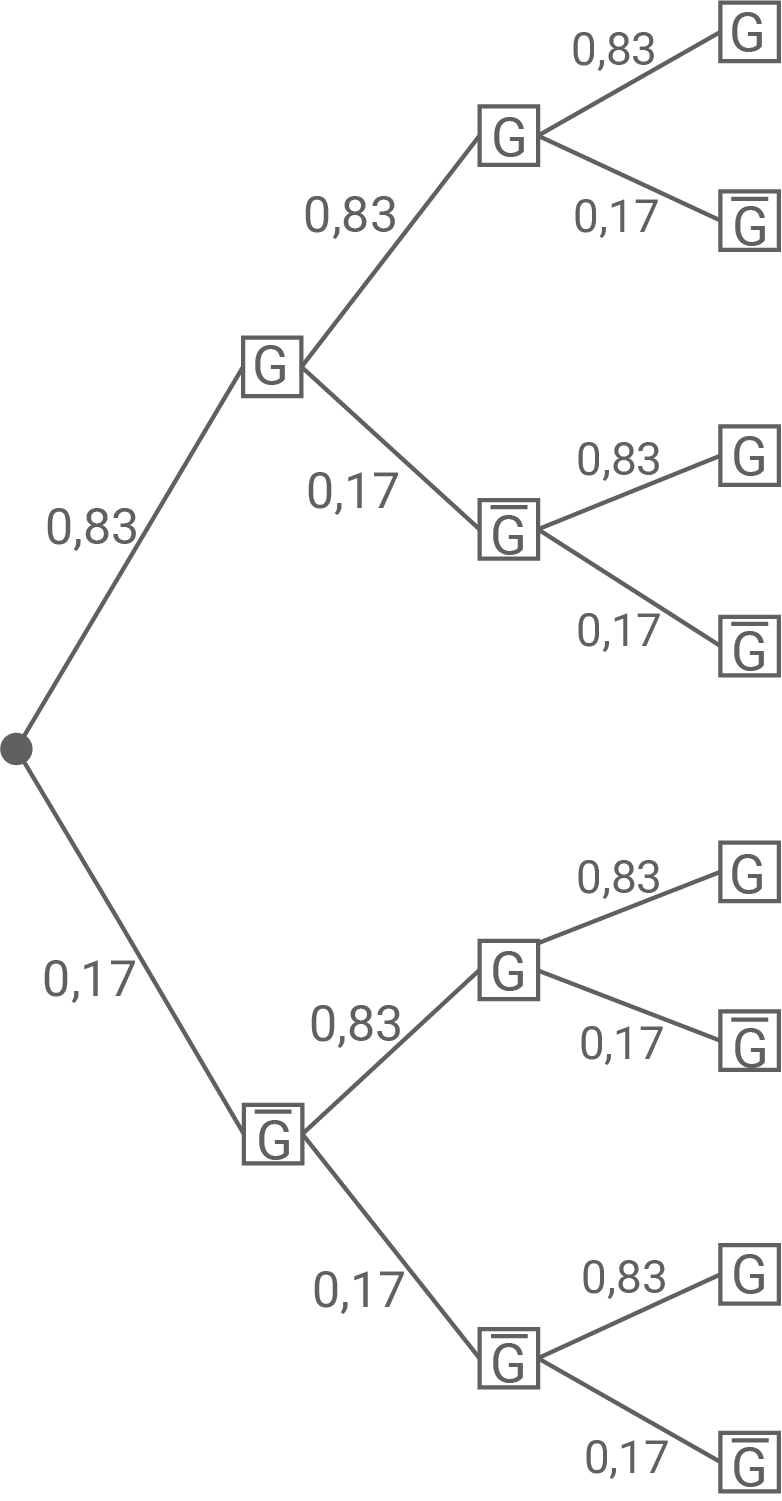
Wahrscheinlichkeitsbaum mit Verzweigungen, Ästen beschriftet mit 0,83 und 0,17 und G‑Kästchen an den Knoten.

Die Zufallsvariable $X$ beschreibt die Anzahl der Frühlingsrollen, die das vorgegebene Gewicht unterschreiten. Sie ist binomialverteilt mit den Parametern $n=3$ und $p=0,17.$

Wahrscheinlichkeit $\boldsymbol{P(X\geq2)}$ berechnen

$\begin{array}[t]{rlll} P(X\geq2) &=& 1-P(X\leq1) \\[5pt] &\approx& 1-0,923 \\[5pt] &=& 0,077 \end{array}$

Somit beträgt die Warscheinlichkeit für das beschriebene Ereignis $7,7\,\%.$

Ein mögliches Zufallsexperiment könnte sein, dass $20$ Frühlingsrollen bestellt werden.

Ein passendes Ereignis könnte sein, dass von den $20$ Frühlingsrollen mindestens eine das vorgegebene Gewicht unterschreitet.

Die Anzahl der Frühlingsrollen, die das vorgegebene Gewicht unterschreiten, ist binomialverteilt mit der Zufallsvariablen $Y$ und den Parametern $p=0,17$ und $n=1500.$

Erwartungswert berechnen

$\begin{array}[t]{rlll} E(Y) &=& 1500 \cdot 0,17 \\[5pt] &=& 255 \end{array}$

Standardabweichung berechnen

$\begin{array}[t]{rlll} \sigma &=& \sqrt{1500 \cdot 0,17 \cdot 0,83} \\[5pt] &\approx& 14,55 \end{array}$

Erwartungswert mit Standardabweichung addieren

$\begin{array}[t]{rlll} E(Y)+\sigma &=& 255+14,55 \\[5pt] &=& 269,55 \end{array}$

Wahrscheinlichkeit berechnen

$\begin{array}[t]{rlll} P(Y\geq270) &=& 1-P(Y\leq269)\\[5pt] &\approx& 1-0,841 \\[5pt] &=& 0,159 \end{array}$

Somit wird mit einer Wahrscheinlichkeit von ungefähr $15,9\,\%$ die Stichprobe beanstandet.

$Z$ beschreibt die Anzahl der Frühlingsrollen, die das vorgegebene Gewicht einhalten und ist binomialverteilt mit $p=0,83$ und unbekanntem $n.$

Gesucht ist das minimale $n,$ sodass gilt:

$\begin{array}[t]{rlll} P(Z \geq 20) &\geq& 0,99 \\[5pt] 1-P(Z \leq 19) &\geq& 0,99 \\[5pt] P(Z \leq 19) &\leq& 0,01 \end{array}$

Systematisches Ausprobieren mit dem Taschenrechner liefert:

$\color{#ffffff}{n}$	$\color{#ffffff}{P(Z\leq19)}$
$29$	$0,018$
$30$	$0,008$

Somit müssen mindestens $30$ Frühlingsrollen gekauft werden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?