Pflichtaufgaben

1 Analysis

Gegeben ist die Funktion $f$ mit $f(x)=x^3+3 x^2, x \in \mathbb{R}.$
$K$ ist der Graph der Funktion.

Berechne

die Koordinaten des Hoch- und des Tiefpunkts von $K$ und
die Steigung von $K$ im Wendepunkt.

(5 BE)

2 Stochastik

In einer Urne befinden sich drei rote und zwei gelbe Kugeln sowie eine blaue Kugel.
Aus dieser Urne werden nacheinander zufällig zwei Kugeln gezogen, ohne sie zurückzulegen, und ihre Farben werden jeweils notiert.

Stelle die Situation durch ein geeignetes beschriftetes Baumdiagramm dar.

(3 BE)

Formuliere im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit sich mit $1-\frac{3}{6} \cdot \frac{2}{5}-\frac{2}{6} \cdot \frac{1}{5}$ berechnen lässt.

(2 BE)

3 Lineare Algebra

Die Punkte $A(5\mid-1\mid 2), B(9\mid2\mid 12)$ und $C(3\mid-2\mid 4)$ sind die Eckpunkte eines Dreiecks $ABC.$

Weise nach, dass das Dreieck $ABC$ bei $C$ einen rechten Winkel besitzt.

(2 BE)

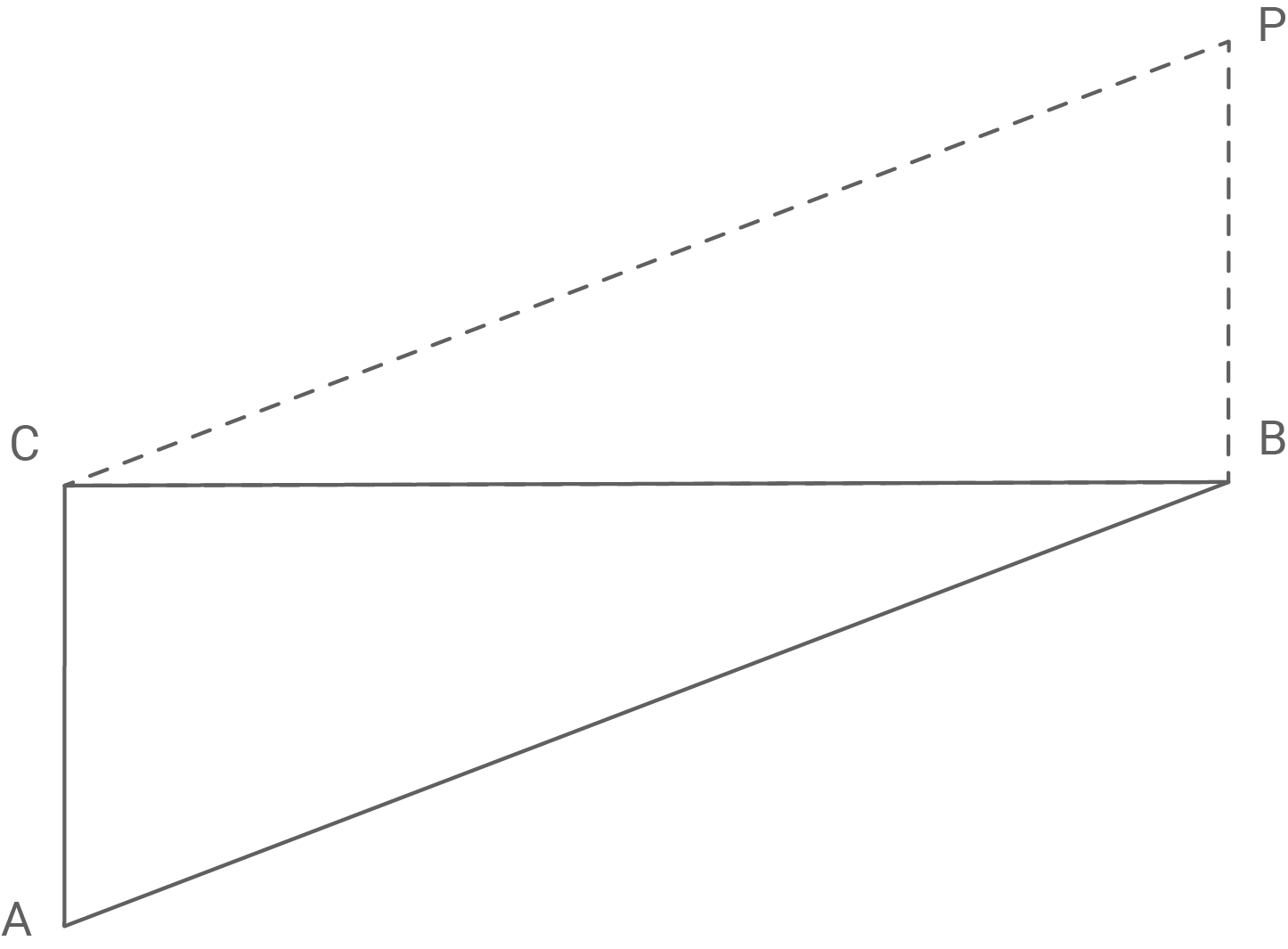
Die abgebildete Skizze stellt das Dreieck $ABC$ dar.

Dreieck mit den Punkten A, B und C, dargestellt in einer einfachen geometrischen Darstellung.

Nun wird ein Punkt $P$ hinzugefügt, sodass dieser zusammen mit $A, B$ und $C$ die Eckpunkte eines Parallelogramms bildet.

Erweitere die Skizze um einen möglichen Punkt $P.$
Bestimme mögliche Koordinaten des Punktes $P$ so, dass das Parallelogramm kein Rechteck ist.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1 Analysis

Hoch- und Tiefpunkt berechnen

Für die ersten beiden Ableitungen von $f$ folgt:

$\(\begin{array}[t]{rlll} f$

Anwenden der notwendigen Bedingung für Extremstellen $\(f$ ergibt:

$\(\begin{array}[t]{rlll} f$

Mit dem Satz des Nullprodukts folgt somit $x_1=0$ und $3x+6=0,$ d.h. $x_2=-2.$ Überprüfen der hinreichenden Bedingung für Extremstellen liefert:

$\(\begin{array}[t]{rlll} f$

Somit besitzt $K$ bei $x=0$ einen Tiefpunkt und bei $x=-2$ einen Hochpunkt. Für die Funktionswerte ergibt sich:

$\begin{array}[t]{rlll} f(0)&=&0^3+3\cdot0^2 \\[5pt] &=&0 \end{array}$

$\begin{array}[t]{rlll} f(-2)&=&(-2)^3+3\cdot(-2)^2 \\[5pt] &=&-8+12 \\[5pt] &=&4 \end{array}$

Die Koordinaten der beiden Extrempunkte von $K$ sind somit durch $T(0\mid0)$ und $H(-2\mid4)$ gegeben.

Steigung im Wendepunkt berechnen

Für die dritte Ableitung von $f$ folgt:

$\(f$

Anwenden der notwendigen Bedingung für Wendestellen $\(f$ ergibt:

$\(\begin{array}[t]{rlll} f$

Da $\(f$ konstant den Wert $6$ besitzt, ist $x=-1$ somit eine Wendestelle von $f.$ Für die Steigung von $K$ im Wendepunkt folgt somit:

$\(\begin{array}[t]{rlll} f$

2 Stochastik

Situation in Baumdiagramm darstellen

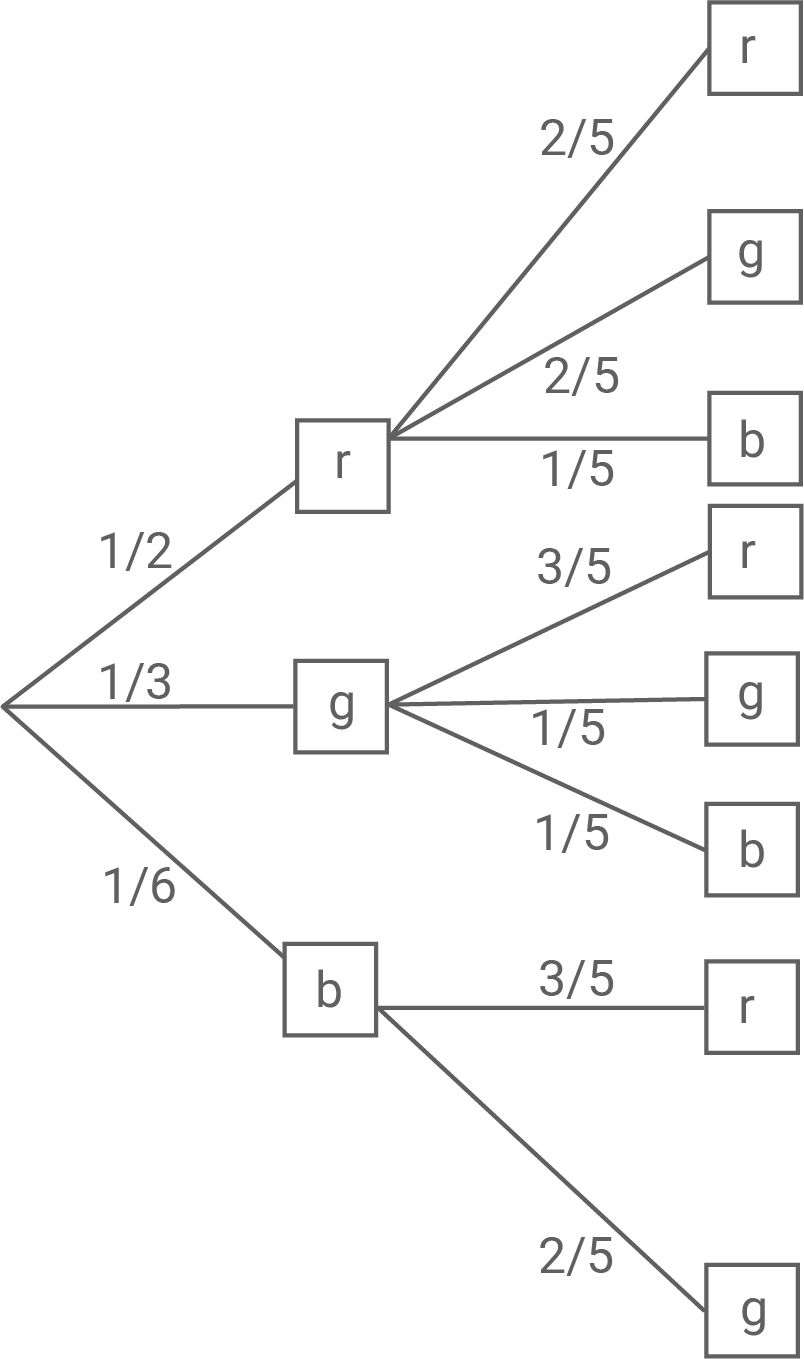
Baumdiagramm mit drei Startknoten r, g, b und Verzweigungen zu r, g, b mit angegebenen Bruchwahrscheinlichkeiten.

$r:$

„Die Kugel ist rot.“

$g:$

„Die Kugel ist grün.“

$b:$

„Die Kugel ist blau.“

Der Teilterm $\frac{3}{6}\cdot\frac{2}{5},$ anders geschrieben auch $\frac{1}{2}\cdot\frac{2}{5},$ beschreibt das Ereignis, dass zweimal eine rote Kugel gezogen wird.
Der Teilterm $\frac{2}{6}\cdot\frac{1}{5},$ anders geschrieben auch $\frac{1}{3}\cdot\frac{1}{5},$ beschreibt das Ereignis, dass zweimal eine grüne Kugel gezogen wird.
In der Urne gibt es nur eine blaue Kugel.
Folglich beschreibt der Term $1-\frac{3}{6}\cdot\frac{2}{5}-\frac{2}{6}\cdot\frac{1}{5}$ das Ereignis „Beide gezogenen Kugeln sind von unterschiedlicher Farbe.“

3 Lineare Algebra

$\begin{array}[t]{rlll} \overrightarrow{CA}&=&\pmatrix{5\\-1\\2}-\pmatrix{3\\-2\\4} \\[5pt] &=&\pmatrix{2\\1\\-2} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{CB}&=&\pmatrix{9\\2\\12}-\pmatrix{3\\-2\\4} \\[5pt] &=&\pmatrix{6\\4\\8} \end{array}$

Für das Skalarprodukt der beiden Vektoren folgt:

$\begin{array}[t]{rlll} \overrightarrow{CA}\circ\overrightarrow{CB}&=&\pmatrix{2\\1\\-2}\circ\pmatrix{6\\4\\8} \\[5pt] &=&12+4-16 \\[5pt] &=&0 \end{array}$

Somit besitzt das Dreick $ABC$ bei $C$ einen rechten Winkel.

Möglichen Punkt einzeichnen

Schematische Darstellung eines rechtwinkligen Dreiecks mit den Punkten A, B, C und einem Punkt P.

Mögliche Koordinaten bestimmen

$\begin{array}[t]{rlll} \overrightarrow{OP}&=&\overrightarrow{OC}+\overrightarrow{AB} \\[5pt] &=&\pmatrix{3\\-2\\4}+\pmatrix{4\\3\\10} \\[5pt] &=&\pmatrix{7\\1\\14} \end{array}$

Mögliche Koordinaten von $P$ sind somit gegeben durch $P(7\mid1\mid14).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?