Wahlaufgaben

5 Analysis

Die Abbildung zeigt den Graphen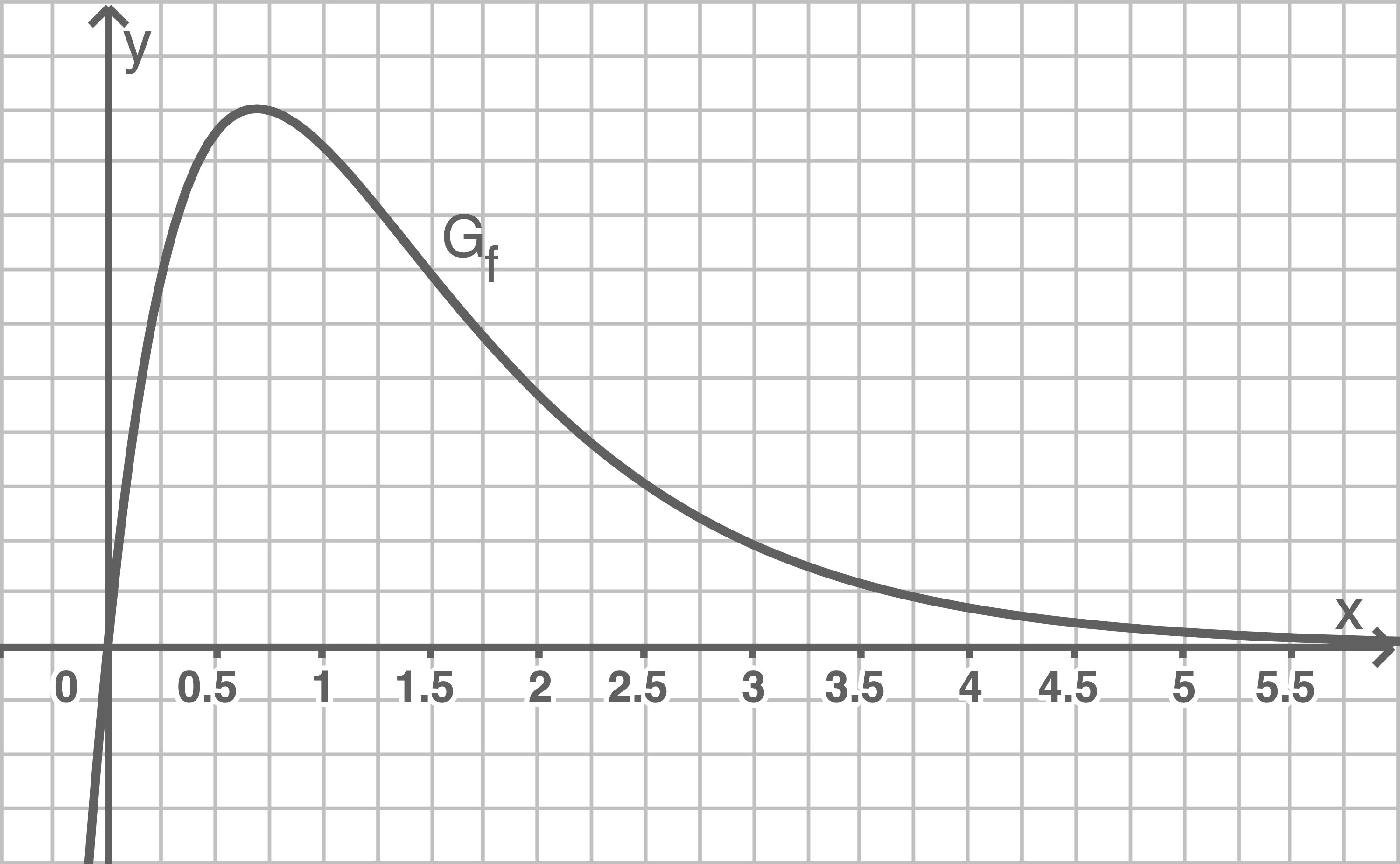 $G_f$ der in $\mathbb{R}$ definierten Funktion $f: x \mapsto \mathrm e^{-x} - \mathrm e^{-2x}.$
$G_f$ schneidet die $x$ -Achse an der Stelle $x_1 = 0$ und hat einen Hochpunkt an der Stelle $x_H.$

baden württemberg berufliches gymnasium abitur 2024

Weise rechnerisch nach, dass $x_1$ die einzige Nullstelle von $f$ ist.

(2 BE)

Entscheide mit Hilfe der Abbildung, ob die folgenden Aussagen wahr oder falsch sind. Begründe jeweils deine Entscheidung.

(1)

$\(f$

(2)

$\displaystyle\int_{0}^{2}f(x)\;\mathrm dx \lt 2 \cdot f(x_H)$

(3 BE)

5 Analysis

Gegeben ist die Funktion $f$ mit $f(x) = (x^2 - 4) \cdot (x - 1)$ mit $x \in \mathbb{R}$ . Ihr Graph ist $K_f$ .

Gib die Nullstellen von $f$ an.

(1 BE)

Betrachtet wird die Tangente an $K_f$ im Schnittpunkt von $K_f$ mit der $y$ -Achse.

Zeige, dass diese Tangente mit $K_f$ einen gemeinsamen Punkt auf der $x$ -Achse hat.

(4 BE)

5 Lineare Algebra

Gegeben sind die beiden $2 \times 2$ -Matrizen $A$ und $B$ sowie der Vektor $\vec{v}$ .

$A = \begin{pmatrix} 2 & -1 \\ -3 & 1 \end{pmatrix},$

$B = \begin{pmatrix} -1 & -1 \\ -3 & -2 \end{pmatrix},$

$\vec{v} = \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}$

Zeige rechnerisch, dass $B$ eine inverse Matrix zu $A$ ist.

(2 BE)

Gib eine mögliche Fragestellung an, die durch die Lösung des folgenden Gleichungssystems beantwortet werden kann:

$\begin{array}[t]{rll} 2v_1 - v_2 &=& 1 & \\[5pt] -3v_1 + v_2 &=& 2 \end{array}$

(3 BE)

5 Lineare Algebra

Für eine reelle Zahl $a$ ist die Gerade $g$ durch $\vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 1 \\ a \end{pmatrix}$ mit $t \in \mathbb{R}$ gegeben.
Außerdem wird die Ebene $E$ beschrieben durch $E: x_1 + x_2 = 3.$

Bestimme den Wert von $a$ so, dass sich $g$ und $E$ orthogonal schneiden.

(2 BE)

Für $a = 1,5$ schneidet $g$ die $x_1$ -Achse im Punkt $P$ und die Ebene $E$ im Punkt $S(1 \mid 2 \mid 3)$ . Zudem ist der Punkt $Q(1 \mid 2 \mid 0)$ bekannt.
Berechne den Flächeninhalt des Dreiecks $PQS$ .

(3 BE)

6 Stochastik

(PLA; mit Hilfsmitteln)

Bearbeite die folgende Aufgabe unter Berücksichtigung der einzelnen Problemlöseschritte. Dokumentiere und reflektiere deine Vorgehensweise.

Drei zufällig mit derselben Wahrscheinlichkeit gewählte, verschiedene Eckpunkte eines regelmäßigen Fünfecks (d.h. alle Seiten sind gleich lang, alle Innenwinkel betragen $108°$ ) werden zu einem Dreieck verbunden.

Untersuche, mit welcher Wahrscheinlichkeit der Mittelpunkt des Fünfecks innerhalb des Dreiecks liegt.

(10 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

5 Analysis

$\begin{array}[t]{rll} f(x)&=& 0 \\[5pt] \mathrm e^{-x}-\mathrm e^{-2x}&=& 0 &\quad \scriptsize \mid\; +\mathrm e^{-2x} \\[5pt] \mathrm e^{-x}&=& \mathrm e^{-2x} &\quad \scriptsize \mid\; \ln(\,)\\[5pt] -x&=& -2x \end{array}$

Diese Gleichung ist nur für $x=0$ erfüllt, damit ist $x_1$ die einzeige Nullstelle von $f.$

(1)

Die Aussage ist falsch.

Der Graph ist an der Stelle $x=0,5$ rechtsgekrümmt, weshalb $\(f$ gelten muss.

(2)

Die Aussage ist wahr.

Es gilt $\displaystyle\int_{0}^{2}f(x_h)\;\mathrm dx=2\cdot f(x_h).$ Da die Funktion $f$ im gegebenen Intervall jedoch einen kleineren Flächeninhalt einschließt als die Funktion $y=f(x_h),$ gilt die angegebene Ungleichung.

5 Analysis

Nach dem Satz vom Nullprodukt sind die Lösungen der Gleichung $f(x)=0$ gegeben durch:

$x_1=2\quad$ $x_2=-2\quad$ $x_3=1$

$f(x)=x^3-x^2-4x+4$

$\(f$

Die allgemeinte Tangentengleichung ist von der Form $y=m\cdot x+c.$

Für die Steigung $m$ gilt:

$\(\begin{array}[t]{rll} m&=& f$

Für den $y$ -Achsenabschnitt $c$ ergibt sich:

$\begin{array}[t]{rll} c&=& f(0)& \\[5pt] &=& (0^2-4)\cdot (0-1)& \\[5pt] &=& 4 \end{array}$

Die Tangente hat also die Gleichung $y=-4x+4.$

Der Schnittpunkt mit der $x$ -Achse ergibt sich zu:

$\begin{array}[t]{rll} 0&=& -4x+4 &\quad \scriptsize \mid\;+4x \\[5pt] 4x&=& 4 &\quad \scriptsize \mid\;:4\\[5pt] x&=& 1 \end{array}$

Nach Teilaufgabe a) schneidet auch der Graph $K_f$ die $x$ -Achse an dieser Stelle. Die Aussage ist somit gezeigt.

5 Lineare Algebra

Rechenweg anzeigen

$\pmatrix{2 & -1\\-3 & 1}\cdot \pmatrix{-1 & -1\\-3 & -2}=\pmatrix{1 & 0\\0 & 1}$

Damit ist gezeigt, dass $B$ eine inverse Matrix zu $A$ ist.

Welche Werte für $v_1$ und $v_2$ lösen die folgende Matrix-Vektor-Gleichung?

$\pmatrix{2& -1\\-3& 1}\pmatrix{v_1\\v_2}=\pmatrix{1\\2}$

5 Lineare Algebra

$g$ und $E$ schneiden sich genau dann orthogonal, wenn das Skalarprodukt des Richtungsvektors der Geraden und des Normalenvektors der Ebene gleich Null ist.

Es gilt:

$\begin{array}[t]{rll} \pmatrix{1\\1\\a}\circ \pmatrix{1\\1\\0}&=& 1\cdot 1+1\cdot 1+0\cdot a&\\[5pt] &=& 2 \end{array}$

Der Wert des Skalarprodukts ist unabhängig von $a$ immer ungleich Null. Es existiert also kein Wert für $a,$ sodass sich $g$ und $E$ orthogonal schneiden.

Koordinaten von $P$ berechnen

$\pmatrix{x_1\\0\\0}=\pmatrix{1\\2\\3}+t\cdot \pmatrix{1\\1\\1,5}$

Aus der zweiten und dritten Zeile folgt direkt $t=-2.$

Daraus ergibt sich für die erste Zeile:

$\begin{array}[t]{rll} x_1 &=& 1+(-2)\cdot 1&\quad \scriptsize \mid\; \\[5pt] &=& -1 \end{array}$

Der Punkt $P$ hat also die Koordinaten $P(-1\mid 0\mid 0).$

Seitenlängen des Dreiecks berechnen

$\overrightarrow{QS}=\pmatrix{1-1\\2-2\\3-0}=\pmatrix{0\\0\\3}$

$\overrightarrow{PQ}=\pmatrix{1-(-1)\\2-0\\0-0}=\pmatrix{2\\2\\0}$

Wegen $\overrightarrow{QS}\circ\overrightarrow{PQ}=0\cdot 2+0\cdot 2+3\cdot 0=0$ handelt es sich um ein rechtwinkliges Dreieck mit Grundseite $|\overrightarrow{QS}|$ und Höhe $|\overrightarrow{PQ}|.$

Mit der Formel für den Flächeninhalt eines Dreiecks folgt:

Rechenweg anzeigen

$A=\dfrac{3}{2}\sqrt{8}$

6 Stochastik

Fünfeck-Eigenschaften:
Ein regelmäßiges Fünfeck hat fünf Eckpunkte. Es gibt $\binom{5}{3}=10$ mögliche Dreiecke, die aus drei dieser Eckpunkte gebildet werden können.
Untersuchung der Dreiecke:

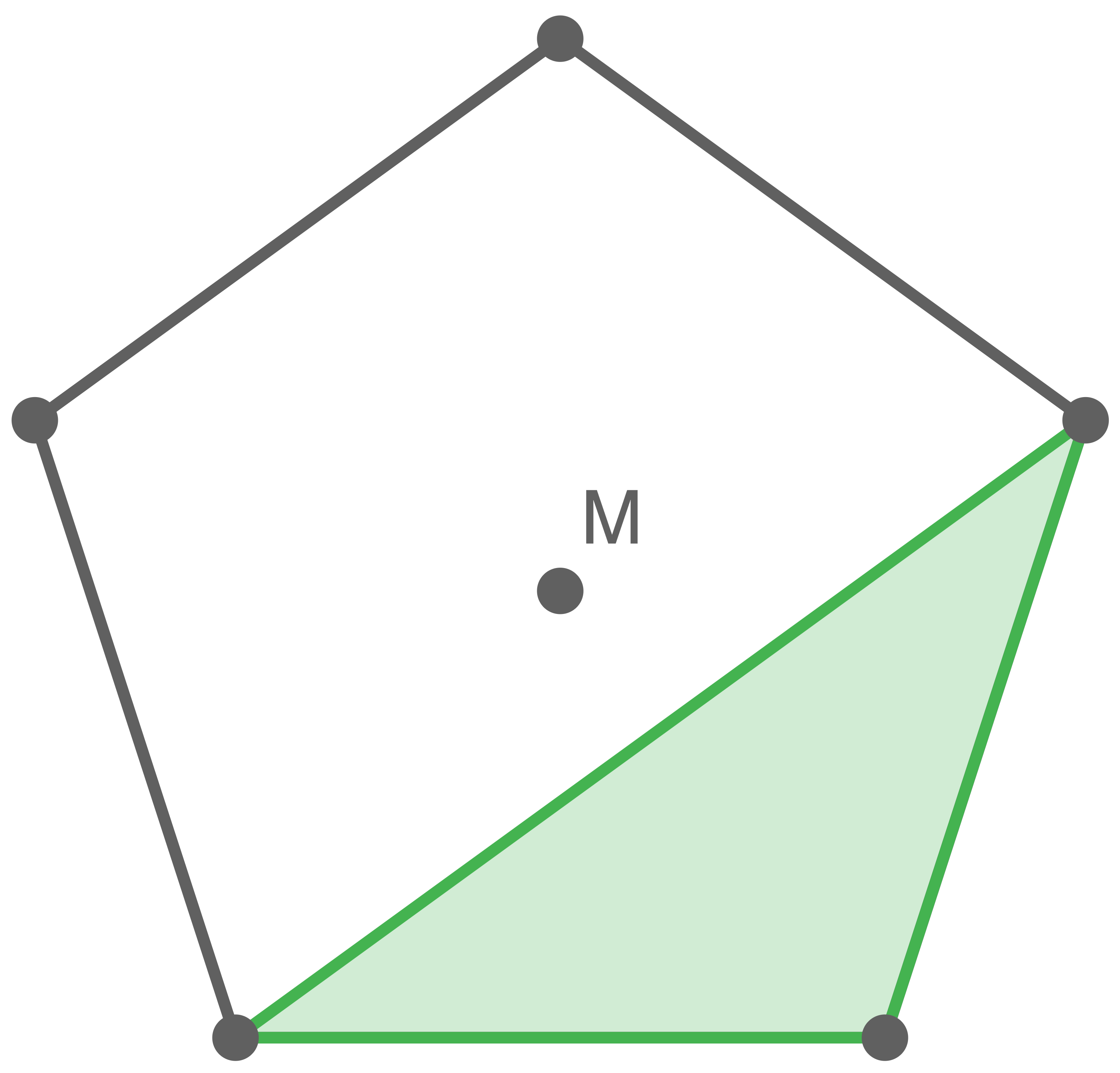
Der Mittelpunkt des Fünfecks liegt in 5 Fällen innerhalb des Dreiecks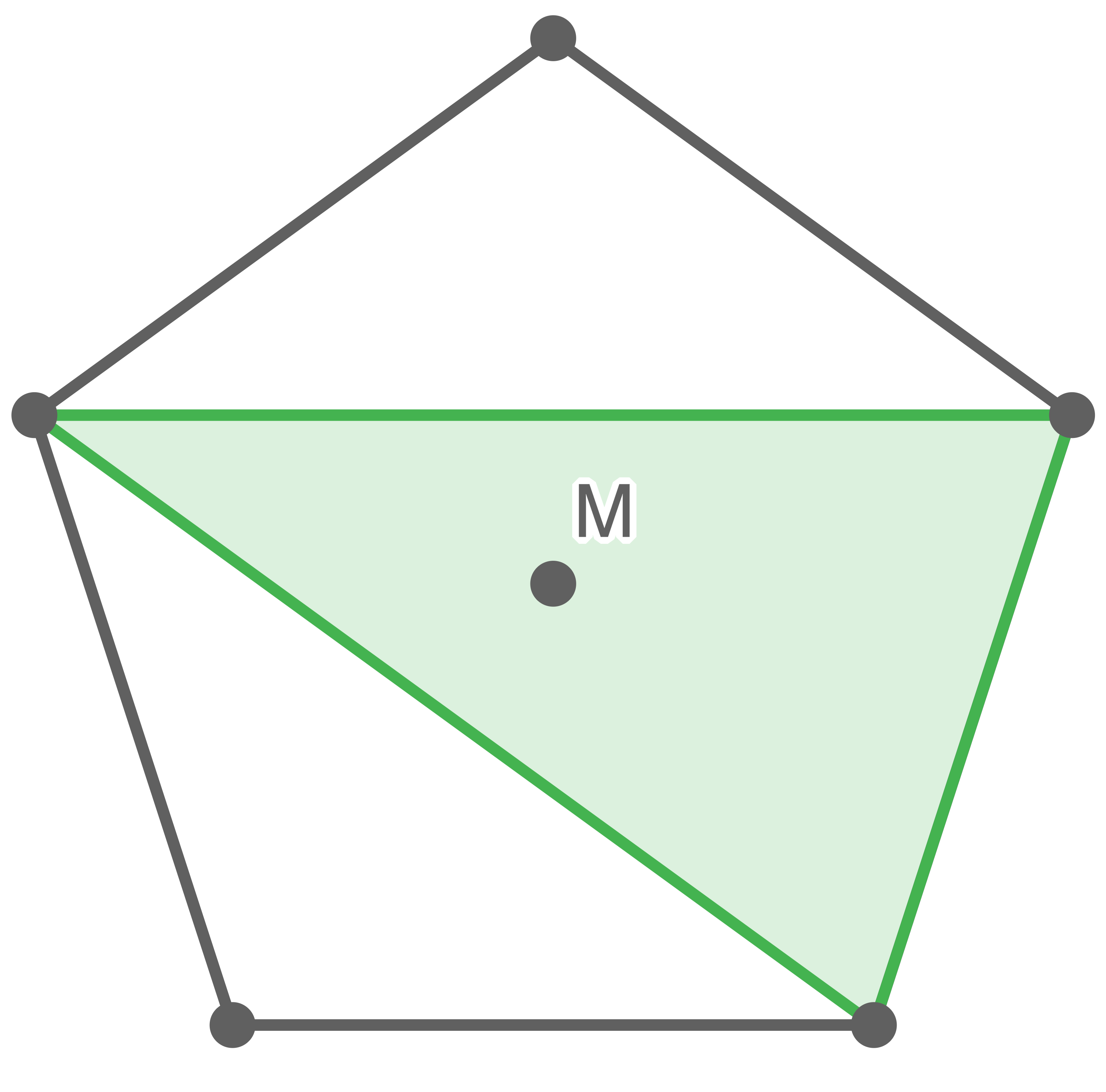

Der Mittelpunkt des Fünfecks liegt in 5 Fällen außerhalb des Dreiecks

Der Mittelpunkt des Fünfecks liegt daher mit einer Wahrscheinlichkeit von $\dfrac{5}{10}=\dfrac{1}{2}$ innerhalb des Dreiecks.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?