Lineare Algebra
Aufgabe III 1
In einem Garten steht ein vollständig verglastes Gewächshaus. Die rechteckige Grundfläche  in der
in der  -Ebene ist
-Ebene ist  Meter
Meter  lang und
lang und  breit. In einer Höhe von
breit. In einer Höhe von  beginnt die Dachschräge, das gesamte Gewächshaus ist
beginnt die Dachschräge, das gesamte Gewächshaus ist  hoch.
hoch.
In der Skizze unten ist die symmetrische Frontansicht des Gewächshauses dargestellt.

In der Skizze unten ist die symmetrische Frontansicht des Gewächshauses dargestellt.

a)
Zeichne das Gewächshaus in ein dreidimensionales Koordinatensystem, wenn die Eckpunkte 




 und
und  bekannt sind.
bekannt sind.
(4 BE)
b)
Berechne das Gewicht des für das Gewächshaus benötigten Glases, wenn ein Quadratmeter Glas  wiegt.
wiegt.
(4 BE)
c)
Berechne den Neigungswinkel für eine der schrägen Dachkanten.
An der Seite des Gewächshauses soll ein dreieckiges, ebenes Sonnensegel angebracht werden. Die Eckpunkte des Sonnensegels sollen sich in den Punkten
(3 BE)
d)
Untersuche, ob der Stumpf gekürzt werden muss, damit das Segel wie geplant gespannt werden kann.
(5 BE)
e)
Zeige, dass es sich bei dem Segel nicht um ein gleichschenkliges Dreieck handelt.
(2 BE)
f)
Bestimme einen Wert für  so dass durch die Verschiebung der Pfostenspitze in den Punkt
so dass durch die Verschiebung der Pfostenspitze in den Punkt  ein gleichschenkliges Dreieck
ein gleichschenkliges Dreieck  entsteht.
entsteht.
(4 BE)
g)
Zur Lösung einer Aufgabe im Zusammenhang mit den Punkten  und
und  ergibt sich folgender Ansatz:
ergibt sich folgender Ansatz:
![\(\begin{array}[t]{rll}
\begin{vmatrix}\pmatrix{5-t\\2-4\\0-3}\end{vmatrix}&=& \begin{vmatrix}\pmatrix{0-t\\2-4\\2-3}\end{vmatrix} &
\end{array}\)](https://www.schullv.de/resources/formulas/8f5908c8caa600d5a7ca9c9fa7ec2d09c8608b45aba1ef8556b005fdb7a6ef39_light.svg) Interpretiere diesen Ansatz.
Interpretiere diesen Ansatz.
(3 BE)
Aufgabe III 2
Gegeben sind die Punkte
a)
Zeige, dass die Geraden  und
und  in einer gemeinsamen Ebene
in einer gemeinsamen Ebene  liegen.
liegen.
(4 BE)
b)
Bestimme eine Koordinatengleichung der in Teilaufgabe a) beschriebenen Ebene  (Zur Kontrolle:
(Zur Kontrolle:  )
)
(3 BE)
c)
Berechne die Koordinaten der Spurpunkte von 
Stelle die Ebene mit Hilfe der Spurpunkte in einem räumlichen Koordinatensystem dar.
mit Hilfe der Spurpunkte in einem räumlichen Koordinatensystem dar.
Die Punkte Stelle die Ebene
(3 BE)
Dieses Quadrat
d)
Zeige, dass ein weiterer Eckpunkt des Quadrats die Koordinaten  hat.
hat.
Berechne die Koordinaten des vierten Eckpunktes.
Berechne die Koordinaten des vierten Eckpunktes.
(5 BE)
e)
Bestimme die Koordinaten einer möglichen Spitze der Pyramide, sodass diese die Höhe  hat.
hat.
Eine weitere gerade Pyramide mit der Grundfläche
(3 BE)
Der Schattenpunkt der Spitze
f)
Begründe, dass der Schattenpunkt  außerhalb der Grundfläche der Pyramide liegt.
außerhalb der Grundfläche der Pyramide liegt.
Berechne die Koordinaten der Spitze
Berechne die Koordinaten der Spitze
(7 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung III 1
a)
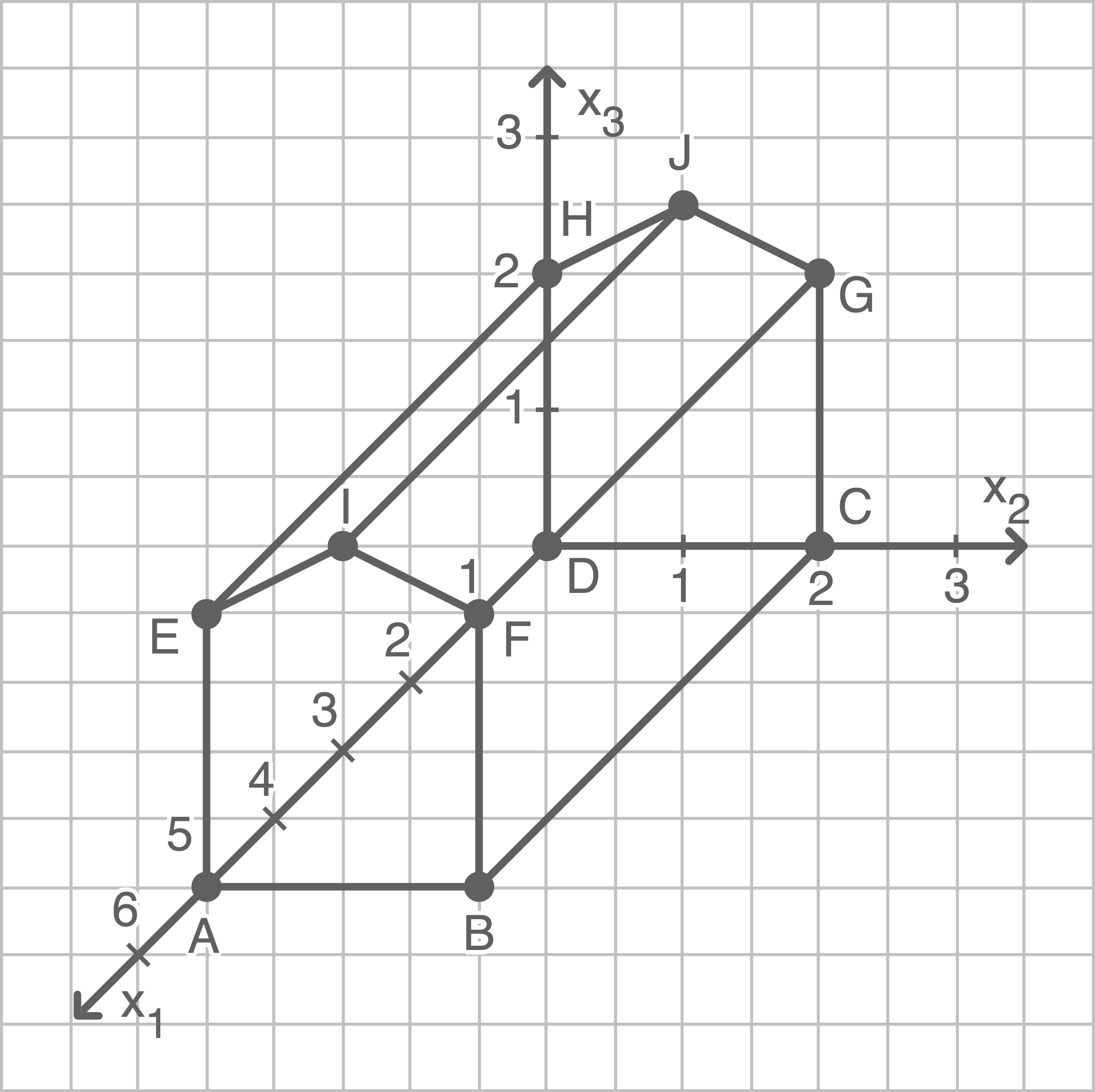
b)
Flächeninhalt der rechteckigen Seitenflächen:
![\(\begin{array}[t]{rll}
A_S&=& 5\,\text{m}\cdot 2\,\text{m} \\[5pt]
&=& 10\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/29ed05f2ed16743084025b7990bf83dcca4e071f1a19b528945aae0d94eb4c29_light.svg) Flächeninhalt der Vorderseite berechnen:
Flächeninhalt der Vorderseite berechnen:
![\(\begin{array}[t]{rll}
A_V&=& (2\,\text{m})^2+\dfrac{1}{2}\cdot 2\,\text{m}\cdot (2,50\,\text{m}-2\,\text{m}) \\[5pt]
&=& 4,50\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/b5420ddd4fbbccd2e651bcfb6abf3f9403665bc57929e4cf85a3a396c01104be_light.svg) Für den Flächeninhalt einer Dachseite muss zunächst die Länge
Für den Flächeninhalt einer Dachseite muss zunächst die Länge  der Dachschräge mit dem Satz des Pythagoras berechnet werden:
der Dachschräge mit dem Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
d^2&=& (2,50\,\text{m}-2\,\text{m})^2+\left(\dfrac{2\,\text{m}}{2}\right)^2 \\[5pt]
d^2&=& 1,25\,\text{m}^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
d&\approx& 1,12\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/dd8e6673f9097e4c2b843cd5b090da5d5aa36ad01dea04b51714f5833ea51faf_light.svg) Damit folgt für den Flächeninhalt einer rechteckigen Dachseite:
Damit folgt für den Flächeninhalt einer rechteckigen Dachseite:
![\(\begin{array}[t]{rll}
A_D&=& 1,12\,\text{m}\cdot 5\,\text{m} \\[5pt]
&=& 5,60\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/f2c33bc6d6f33e30bb3b3b657f7f36ed48d665e2a5e2f9a0dfbf631cccd1bd6d_light.svg) Für den Flächeninhalt der Gesamtoberfläche des Gewächshauses folgt:
Für den Flächeninhalt der Gesamtoberfläche des Gewächshauses folgt:
![\(\begin{array}[t]{rll}
A&=& 2\cdot (4,50\,\text{m}^2+1,12\,\text{m}+5,60\,\text{m}^2) \\[5pt]
&=& 22,44\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/eb04bc6a7f5ec7313ba4fa5dccd88d23f343474705ba623e838456d89ea84e9b_light.svg) Für das Gewicht des benötigten Glases gilt schließlich:
Für das Gewicht des benötigten Glases gilt schließlich:

c)
Steigung der Dachkanten berechnen:
 Der Neigungswinkel
Der Neigungswinkel  lässt sich nun wie folgt berechnen:
lässt sich nun wie folgt berechnen:
![\(\begin{array}[t]{rll}
\tan(\theta)&=& 0,5 & \quad \scriptsize \mid\; \arctan \\[5pt]
\theta&=& \arctan(0,5) \\[5pt]
\theta&\approx& 26,57^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/68a61f55375f89ae3202cd63cb41bbac67f61b33002765e75cf0fd28078d6d62_light.svg)
d)
e)
f)
Es handelt sich um ein gleichschenkliges Dreieck, wenn der Abstand zwischen  und
und  gleich dem Abstand zwischen
gleich dem Abstand zwischen  und
und  ist.
Mit der pq-Formel folgt:
ist.
Mit der pq-Formel folgt:
![\(\begin{array}[t]{rll}
k_{1,2}&=& -\dfrac{-4}{2}\pm\sqrt{\left(\dfrac{-4}{2}\right)^2-(-16,75)} \\[5pt]
&=& 2\pm\sqrt{20,75} \\[5pt]
k_1&\approx& 6,56 \\[5pt]
k_2&\approx& -2,56
\end{array}\)](https://www.schullv.de/resources/formulas/143b4558d72cc406ea768939788ebe4f00931f172608bda0a3bffa5c8c63f95c_light.svg) Für diese Werte von
Für diese Werte von  ist das Dreieck
ist das Dreieck  gleichschenklig.
gleichschenklig.
g)
Gesucht ist ein Wert für  sodass die Punkte
sodass die Punkte  und
und  vom Punkt
vom Punkt  jeweils den gleichen Abstand haben. Dafür wird der Betrag der jeweiligen Differenzen gleichgesetzt.
jeweils den gleichen Abstand haben. Dafür wird der Betrag der jeweiligen Differenzen gleichgesetzt.
Lösung III 2
a)
b)
Ein Normalenvektor von  ergibt sich durch das Kreuzprodukt der Richtungsvektoren von
ergibt sich durch das Kreuzprodukt der Richtungsvektoren von  und
und  Die Ebenengleichung ist also von der Form
Die Ebenengleichung ist also von der Form  Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  liefert:
liefert:
 Die Ebenengleichung ist gegeben durch
Die Ebenengleichung ist gegeben durch 
c)
Spurpunkte berechnen
![\(\begin{array}[t]{rll}
2x_1+2\cdot 0+0&=& 6 &\quad \scriptsize \mid\; :2 \\[5pt]
x_1&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/98f6c6050dc63861931ead867ff52dde1c52058c9e979c237c7271fdae4f2b37_light.svg)
![\(\begin{array}[t]{rll}
2\cdot 0+2x_2+0&=& 6 &\quad \scriptsize \mid\; :2 \\[5pt]
x_2&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/899fe103c6b1cd350154ee113d043fbc40b5ee7cceb5770d2f23aaf2f7caa60a_light.svg)
![\(\begin{array}[t]{rll}
2\cdot 0+2\cdot 0+x_3&=& 6 \\[5pt]
x_3&=& 6
\end{array}\)](https://www.schullv.de/resources/formulas/9789cad4c4ea128b6814b0323508245759a4e58f03ca2e0e61869f87f2d8d232_light.svg) Ebene
Ebene  darstellen
darstellen
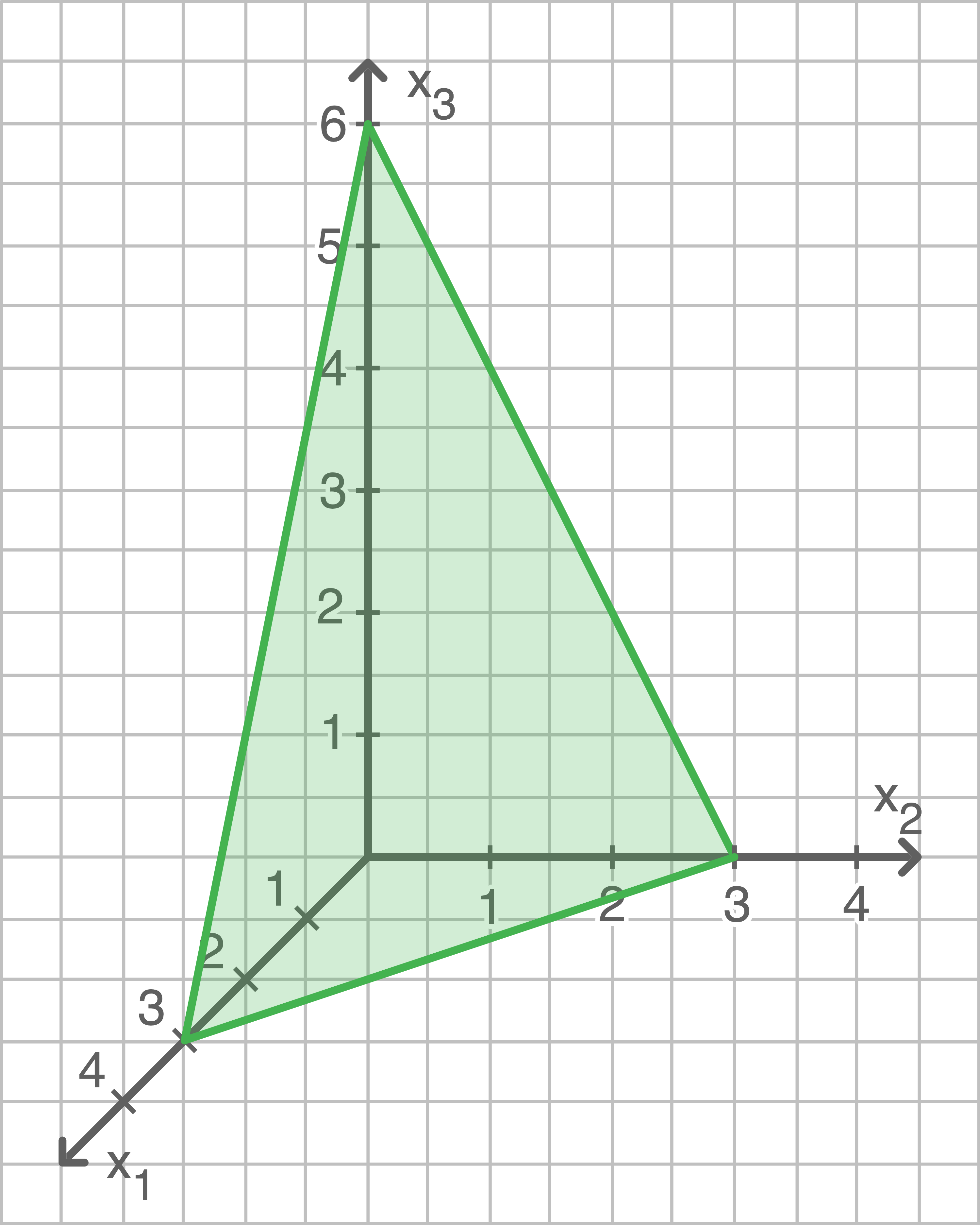

d)
Koordinaten bestätigen
![\(\begin{array}[t]{rll}
M&=&\left(\dfrac{0+2}{2}, \dfrac{3+(-1)}{2}, \dfrac{0+4}{2}\right) & \\[5pt]
&=& (1\mid 1\mid 2)
\end{array}\)](https://www.schullv.de/resources/formulas/20b1547314bde3a1836030ca07d5750a42dc54b8b312ffc74fe636c329d86948_light.svg)

 Mit den gegebenen Koordinaten
Mit den gegebenen Koordinaten  folgt:
folgt:

 Außerdem gilt:
Da
Außerdem gilt:
Da  und
und  die gleiche Länge haben und orthogonal zueinander stehen, ist der Punkt
die gleiche Länge haben und orthogonal zueinander stehen, ist der Punkt  ein weiterer Eckpunkt des Quadrats.
Koordinaten des vierten Eckpunkts berechnen
ein weiterer Eckpunkt des Quadrats.
Koordinaten des vierten Eckpunkts berechnen
![\(\begin{array}[t]{rll}
\overrightarrow{OD}&=& \overrightarrow{OM}-\overrightarrow{MB} \\[5pt]
&=& \pmatrix{1\\1\\2}-\pmatrix{-2\\1\\2} \\[5pt]
&=& \pmatrix{3\\0\\0}
\end{array}\)](https://www.schullv.de/resources/formulas/7765486fffb3d780bc5660a8e6a7ce1a9fa93003dda42a788c97f9d6ca42e9d9_light.svg) Der vierte Eckpunkt hat die Koordinaten
Der vierte Eckpunkt hat die Koordinaten 
e)
f)
Lage des Schattenpunkts begründen
Die kleinste  -Koordinate der Eckpunkte des Vierecks ist
-Koordinate der Eckpunkte des Vierecks ist  Für die
Für die  -Koordinate aller Punkte innerhalb des Quadrats muss also
-Koordinate aller Punkte innerhalb des Quadrats muss also  gelten. Da für
gelten. Da für  aber
aber  gilt, kann der Schattenpunkt nicht innerhalb der Grundfläche der Pyramide liegen.
Koordinaten von
gilt, kann der Schattenpunkt nicht innerhalb der Grundfläche der Pyramide liegen.
Koordinaten von  berechnen
Die
berechnen
Die  - und
- und  -Koordinaten der Spitze
-Koordinaten der Spitze  stimmen mit den Koordinaten des Schattenpunkts
stimmen mit den Koordinaten des Schattenpunkts  überein, weil der Schatten in der
überein, weil der Schatten in der  -Richtung auf die Ebene
-Richtung auf die Ebene  projiziert wird. Der Punkt
projiziert wird. Der Punkt  liegt also auf der Geraden mit der folgenden Gleichung:
liegt also auf der Geraden mit der folgenden Gleichung:
 Da der Punkt
Da der Punkt  auf der Geraden senkrecht zur Ebene
auf der Geraden senkrecht zur Ebene  durch den Punkt
durch den Punkt  läuft, liegt
läuft, liegt  außerdem auf der folgenden Geraden:
außerdem auf der folgenden Geraden:
 Gleichsetzen der Geradengleichungen liefert:
Gleichsetzen der Geradengleichungen liefert:
 Aus der ersten und zweiten Zeile folgt:
Aus der ersten und zweiten Zeile folgt:
![\(\begin{array}[t]{rll}
3&=& 1+2s &\quad \scriptsize \mid\;-1 \\[5pt]
2&=& 2s &\quad \scriptsize \mid\;:2 \\[5pt]
1&=& s
\end{array}\)](https://www.schullv.de/resources/formulas/41dee546dffd192a4b9ea27a87ca1c2d8923dd1083f774fddd117b47c1f4ee3d_light.svg) Aus der dritten Zeile ergibt sich somit:
Aus der dritten Zeile ergibt sich somit:
![\(\begin{array}[t]{rll}
-6+r&=& 2+1 &\quad \scriptsize \mid\;+6 \\[5pt]
r&=& 9
\end{array}\)](https://www.schullv.de/resources/formulas/884eb91030628d0e2538b9cd33f2bad96d8199bf0534ba30e8242a1285de1649_light.svg) Einsetzen in beispielsweise die Geradengleichung von
Einsetzen in beispielsweise die Geradengleichung von  liefert:
liefert:
 Die Spitze der Pyramide hat also die Koordianten
Die Spitze der Pyramide hat also die Koordianten 