Stochastik

Aufgabe II 1

Bei einem Marathonlauf kommen erfahrungsgemäß $77 \%$ der Teilnehmer im Ziel an.
Untersucht wird eine Gruppe von 150 zufällig ausgewählten Teilnehmern. Die Zufallsgröße $X$ beschreibt die Anzahl der Teilnehmer dieser Gruppe, die im Ziel ankommen.

Es gilt: $P(X \gt 115) \approx 50{,}7 \%.$

Interpretiere diese Aussage im Sachzusammenhang.

(2 BE)

Berechne jeweils die Wahrscheinlichkeiten der folgenden Ereignisse:

Aus dieser Gruppe kommen genau 110 Teilnehmer im Ziel an.

Aus dieser Gruppe kommen weniger als 119 Teilnehmer im Ziel an.

(4 BE)

Jeder der 45 000 Teilnehmer, der im Ziel ankommt, erhält ein Finisher-Shirt.
$Y$ beschreibt die Anzahl an ausgegebenen Finisher-Shirts.
Bestimme die Wahrscheinlichkeit, dass $Y$ um weniger als eine halbe Standardabweichung vom Erwartungswert abweicht.

(6 BE)

Von den Teilnehmern, die nicht im Ziel angekommen sind, haben

$82\,\%$ wegen „mangelnder Vorbereitung“
$72\,\%$ entweder wegen „mangelnder Vorbereitung“ oder wegen „Schmerzen während des Laufs“
$13\,\%$ weder wegen „mangelnder Vorbereitung“ noch wegen „Schmerzen während des Laufs“

den Lauf abgebrochen.

Zeige, dass $20 \%$ derjenigen, die nicht im Ziel angekommen sind, den Lauf wegen „Schmerzen während des Laufs“ abgebrochen haben.
Untersuche, ob die Ereignisse „mangelnde Vorbereitung“ und „Schmerzen während des Laufs“ stochastisch unabhängig sind.

(5 BE)

$34 \%$ der Teilnehmer, die den Lauf beenden, sind Frauen. Betrachtet wird eine Gruppe von 1000 Teilnehmern, die den Lauf beendet haben. Ermittle die größte natürliche Zahl $k,$ sodass die Wahrscheinlichkeit, dass sich in dieser Gruppe weniger als $k$ Frauen befinden, kleiner als $20\,\%$ ist.

(4 BE)

Die Laufzeit einer Frau, die im Ziel ankommt, wird durch eine normalverteilte Zufallsgröße mit einer Standardabweichung von $44\,\text{min}$ beschrieben.
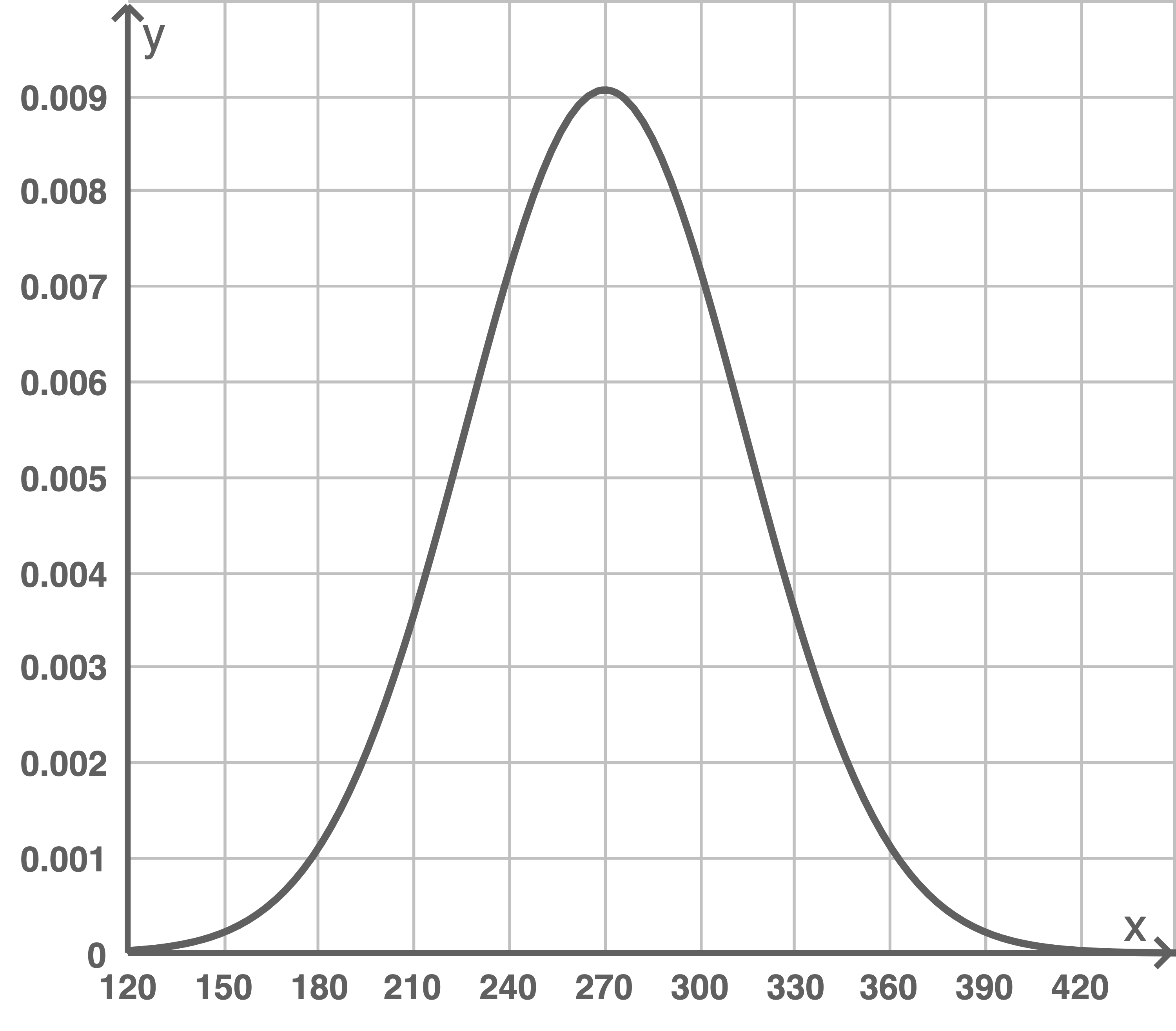
Die Abbildung zeigt den Graphen einer zugehörigen Dichtefunktion.
Ermittle näherungsweise die Wahrscheinlichkeit, dass die Laufzeit einer Frau zwischen vier und fünf Stunden beträgt.
Beurteile die folgende Aussage: „Der Abbildung entnimmt man, dass die Wahrscheinlichkeit einer Zeit von genau vier Stunden etwa $0,7\,\%$ beträgt.“

baden württemberg berufliches gymnasium abitur 2024

(4 BE)

Aufgabe II 2

Ein Unternehmen lässt ein neues Pflegeprodukt auf Verträglichkeit prüfen. Tests ergaben, dass $91\,\%$ der Anwender das Produkt vertragen. Bei den anderen Anwendern trat eine Unverträglichkeit auf.

Es werden nacheinander 20 zufällig ausgewählte Testpersonen befragt.
Berechne für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:

$E_1:$

Nur die dritte Testperson verträgt das Produkt nicht.

$E_2:$

Genau $18$ Testpersonen vertragen das Produkt.

$E_3:$

Mindestens $70\,\%$ der Testpersonen vertragen das Produkt.

(5 BE)

200 Personen nutzen das Pflegeprodukt. Berechne die Wahrscheinlichkeit, dass dabei die Anzahl der Personen, die das Produkt nicht vertragen, zwischen 14 und 22 liegt.

(3 BE)

Bei den Unverträglichkeiten der Testpersonen kann es sich um eine Allergie $(A)$ oder um eine Irritation $(I)$ handeln. Beide Unverträglichkeiten können einzeln oder auch gemeinsam auftreten. Bei $5,5\,\%$ aller Testpersonen tritt eine Allergie auf. Von diesen haben $90\,\%$ keine Irritation.

	$A$	$\overline{A}$	$\Sigma$
$I$
$\overline{I}$		$0,91$
$\Sigma$

Übertrage die Vierfeldertafel auf dein Blatt und vervollständige diese.
$($ Zur Kontrolle: $P(A \cap I) = 0{,}0055)$

(3 BE)

Zeige, dass das Auftreten der beiden Unverträglichkeiten stochastisch abhängig voneinander ist.

(2 BE)

Berechne die Wahrscheinlichkeit, dass entweder eine Allergie oder eine Irritation auftritt.

(3 BE)

Nachdem eine Testperson das Pflegeprodukt anwendet, tritt bei ihr eine Irritation auf. Ermittle, mit welcher Wahrscheinlichkeit sie auch allergisch reagiert.

(2 BE)

Die Kosten für die Herstellung des Pflegeprodukts betragen $0,50\,€$ pro Stück, der Kaufpreis $9,50\,€$ pro Stück. Das Unternehmen erstattet den gesamten Kaufpreis, wenn der Kunde dies begründet beantragt. Dafür muss angegeben werden, ob dies entweder aufgrund einer Unverträglichkeit oder aus sonstigen Gründen geschieht. Alle Kunden mit auftretender Unverträglichkeit beantragen eine Rückerstattung.

Das Unternehmen möchte einen durchschnittlichen Gewinn von mindestens $6,50\,€$ pro Stück erwirtschaften.
Berechne, wie groß der Anteil aller Kunden höchstens sein darf, welche die Rückerstattung aus sonstigen Gründen beantragen.

(7 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung II 1

Mit einer Wahrscheinlichkeit von über $50\,\%$ kommen mehr als 115 Teilnehmer der Gruppe im Ziel an.

$P(A)=P(X=110)\approx0,042=4,2\,\%$

$P(B)=P(X\leq 118)\approx 0,716=71,6\,\%$

Erwartungswert berechnen:

$E(Y)=45\,000 \cdot 0,77=34\,650$

Eine halbe Standardabweichung ergibt sich zu:

$\dfrac{1}{2}\cdot \sigma(Y)=\dfrac{1}{2}\sqrt{45000 \cdot 0,77 \cdot 0,23} \approx 44,6$

Es gilt also:

$34\,650-44,6=34\,605,4$

$34\,650+44,6=34\,694,6$

Damit folgt für die gesuchte Wahrscheinlichkeit:

$\begin{array}[t]{rll} && P(34\,606\leq Y\leq 34\,694) \\[5pt] &=& P(Y\leq 34\,694)-P(Y\leq 34\,605)\\[5pt] &\approx& 0,6907-0,3088 \\[5pt] &=& 0,3819 \end{array}$

Die Wahrscheinlichkeit beträgt also ca. $38,19\,\%.$

Wahrscheinlichkeit zeigen

$A:$ Ereignis, dass jemand den Lauf wegen "mangelnder Vorbereitung" abgebrochen hat.

$B:$ Ereignis, dass jemand den Lauf wegen "Schmerzen während des Laufs" abgebrochen hat.

Die folgenden Werte lassen sich direkt in eine Vierfeldertafel eintragen:

	$B$	$\overline{B}$	$\Sigma$
$A$			$\boldsymbol{0,82}$
$\overline{A}$	$0,05$	$\boldsymbol{0,13}$	$0,18$
$\Sigma$			$\boldsymbol{1}$

Weiter ist bekannt, dass die Summe der Wahrscheinlichkeiten $P(\overline{A}\cap B)$ und $P(A\cap \overline{B})$ insgesamt $72\,\%$ beträgt. Wegen $P(\overline{A}\cap B)=0,05$ folgt für die Wahrscheinlichkeit von $P(A\cap \overline{B}):$

$P(A\cap \overline{B})=0,72-0,05=0,67$

Damit lässt sich die Vierfeldertafel wie folgt vervollständigen:

	$B$	$\overline{B}$	$\Sigma$
$A$	$0,15$	$0,67$	$\boldsymbol{0,82}$
$\overline{A}$	$0,05$	$\boldsymbol{0,13}$	$0,18$
$\Sigma$	$0,20$	$0,80$	$\boldsymbol{1}$

Es gilt also $P(B)=20\,\%,$ damit ist die Aussage gezeigt.

Stochastische Unabhängigkeit überprüfen

$P(A\cap B)=0,15$

$P(A)\cdot P(B)=0,82\cdot 0,20=0,164$

Wegen $P(A\cap B)\neq P(A)\cdot P(B)$ sind die beiden Ereignisse $A$ und $B$ stochastisch abhängig.

Die Zufallsvariable $X$ gibt die Anzahl der Frauen an. $X$ ist binomialverteilt mit $n=1000$ und $p=0,34.$

Gesucht ist der größte Wert für $k,$ sodass gilt:

$\begin{array}[t]{rll} P(X\lt k)&\lt& 0,2 \\[5pt] P(X\leq k-1)&\lt& 0,2 \end{array}$

Systematisches Ausprobieren mit dem Taschenrechner liefert:

$k=327:$

$P(X\leq 326)=0,1839$

$k=328:$

$P(X\leq 327)=0,2023$

Der gesuchte Wert ist somit $k=327.$

Wahrscheinlichkeit für Laufzeit ermitteln

Die Laufzeit zwischen 4 und 5 Stunden entspricht der Laufzeit zwischen 240 und 300 Minuten. Die zugehörige Wahrscheinlichkeit ist gegeben durch den Flächeninhalt unter der Dichtefunktion in diesem Intervall.

Dieser entspricht ungefähr 17 Kästchen.

Ein Kästchen entspricht $30\cdot 0,001=0,03$

Die gesuchte Wahrscheinlichkeit ergibt sich zu:

$17\cdot 0,03=0,51$

Die Wahrscheinlichkeit, dass die Laufzeit einer Frau zwischen 4 und 5 Stunden liegt, beträgt ungefähr $50\,\%.$

Aussage beurteilen

Die Aussage ist falsch, da bei einer stetigen Verteilung wie der Normalverteilung die Wahrscheinlichkeit für einen exakten Wert, wie genau 4 Stunden, immer 0 ist.

Lösung II 2

$\begin{array}[t]{rll} P(E_1)&=& 0,91^{19}\cdot 0,09&\\[5pt] &\approx & 0,015&\\[5pt] &=&1,5\,\% \end{array}$

$\begin{array}[t]{rll} P(E_2)&=& \binom{20}{18} \cdot 0,91^{18} \cdot 0,09^2&\\[5pt] &\approx & 0,231&\\[5pt] &=&23,1\,\% \end{array}$

Für $E_3$ ist die Wahrscheinlichkeit gesucht, dass mindestens $70\,\%$ der 20 Personen das Produkt vertragen:

$0,7\cdot 20=14$

Die Zufallsvariable $X$ gibt die Anzahl der Personen an, die das Produkt vertragen und ist binomialverteilt mit $n=20$ und $p=0,91.$

Damit folgt für die gesuchte Wahrscheinlichkeit:

$P(X\geq 14)\approx 0,9987=99,87\,\%$

Die Zufallsvariable $Y$ gibt die Anzahl der Personen an, die das Produkt nicht vertragen und ist binomialverteilt mit $n=200$ und $p=0,09.$

$\begin{array}[t]{rll} &&P(14\leq Y \leq 22)\\[5pt] &=& P(Y\leq 22)-P(Y\leq 13) \\[5pt] &\approx & 0,8657-0,1308 \\[5pt] &=& 0,7349 \end{array}$

Die Wahrscheinlichkeit beträgt ungefähr $73,5\,\%.$

Eintragen des bekannten Werts $P(A)=0,055$ und Ergänzen der Wahrscheinlichkeiten liefert zunächst:

	$A$	$\overline{A}$	$\Sigma$
$I$		$0,035$
$\overline{I}$		$0,91$
$\Sigma$	$0,055$	$0,945$	$1$

Mit Hilfe der in der Aufgabenstellung gegebenen Wahrscheinlichkeiten folgt weiter:

$\begin{array}[t]{rll} P(A\cap \overline{I})&=& P_A(\overline{I})\cdot P(A) \\[5pt] &=& 0,9\cdot 0,055 \\[5pt] &=& 0,0495 \end{array}$

Damit folgt insgesamt:

	$A$	$\overline{A}$	$\Sigma$
$I$	$0,0055$	$0,035$	$0,0405$
$\overline{I}$	$0,0495$	$0,91$	$0,9595$
$\Sigma$	$0,055$	$0,945$	$1$

$P(A\cap I)=0,0055$

$P(A)\cdot P(I)=0,055\cdot 0,0405\approx 0,0022$

Wegen $P(A\cap I)\neq P(A)\cdot P(I)$ ist das Auftreten der Unverträglichkeiten stochastisch abhängig voneinander.

$\begin{array}[t]{rll} && P(A\cap \overline{I})+ P(\overline{A}\cap I)\\[5pt] &=& 0,0495+0,035 \\[5pt] &=& 0,0845 \end{array}$

Die Wahrscheinlichkeit beträgt somit $8,45\,\%.$

$\begin{array}[t]{rll} P_I(A)&=& \dfrac{P(A\cap I)}{P(I)} \\[5pt] &=& \dfrac{0,0055}{0,0405} \\[5pt] &\approx& 0,1358 \end{array}$

Die Wahrscheinlichkeit beträgt ungefähr $13,6\,\%.$

Der Gewinn pro Stück beträgt $9,50\,€-0,50\,€=9,00\,€.$

Bei einer Rückerstattung verliert das Unternehmen den Wert der Herstellungskosten von $0,50\,€.$

Die Wahrscheinlichkeit, dass ein Kunde das Produkt nicht verträgt, beträgt $0,09$ . Der durchschnittliche Gewinn pro verkaufter Einheit sollte mindestens $6,50\,€$ betragen.

Daher ergibt sich mit der Wahrscheinlichkeit $p_s$ für Kunden, die eine Rückerstattung aus sonstigen Gründen beantragen:

Rechenweg anzeigen

$p_s\approx 0,17$

Der Anteil der Kunden, die eine Rückerstattung aus sonstigen Gründen beantragen, darf maximal $17\,\%$ betragen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?