B1 – Analysis

Gegeben ist die in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierte Funktion $Formula: f : x ↦ \tfrac{1}{100}\cdot\left(2x^3 − 43x^2 + 248x\right).$ $Formula: f : x ↦ \tfrac{1}{100}\cdot\left(2x^3 − 43x^2 + 248x\right).$ Abbildung 1 zeigt den Graphen Formula: G_f von im Bereich $Formula: 0 \leq x \leq 10.$ $Formula: 0 \leq x \leq 10.$

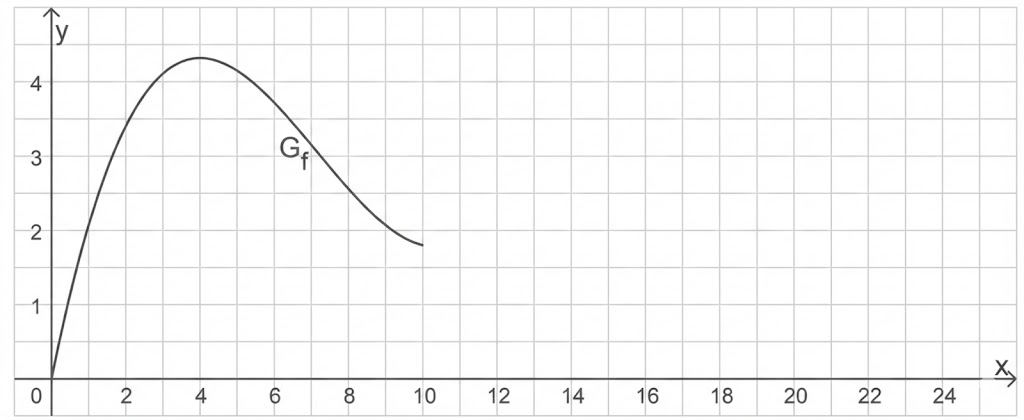
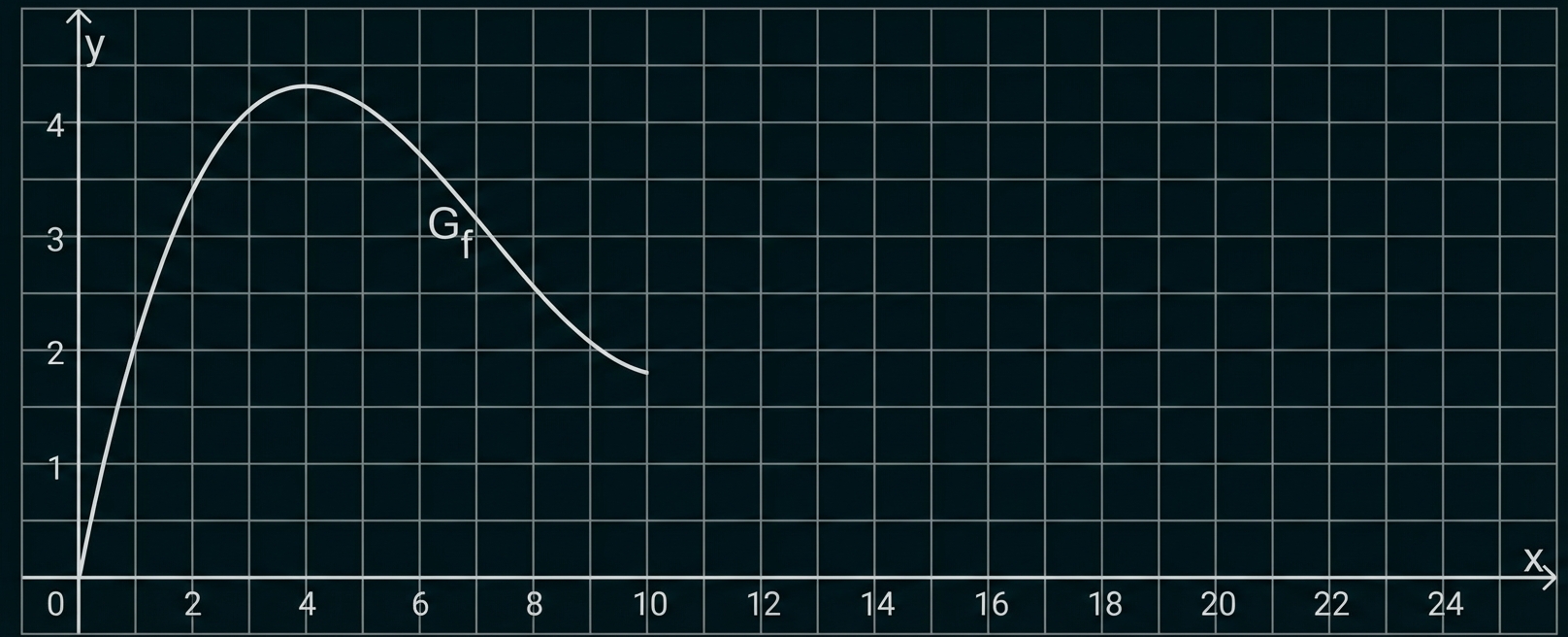
Koordinatensystem mit G_f-Kurve: steigt zu einem Gipfel bei x≈3–4, fällt danach, beschriftete Achsen und Gitternetz.

Abb. 1

Begründe anhand des Terms von Formula: f, dass Formula: G_f nicht symmetrisch bezüglich des Koordinatenursprungs ist, und zeige rechnerisch, dass für $Formula: x \lt 7\tfrac{1}{6}$ $Formula: x \lt 7\tfrac{1}{6}$ rechtsgekrümmt ist.

4 BE

Es gibt eine Stelle $Formula: x_0 \in [0;10],$ $Formula: x_0 \in [0;10],$ an der die lokale Änderungsrate von Formula: f mit der mittleren Änderungsrate von im Intervall Formula: [0;10] übereinstimmt. Ermittle grafisch anhand von Abbildung 1 einen Näherungswert für Formula: x_0.

3 BE

Bestimme eine Gleichung der Tangente Formula: t an Formula: G_f im Punkt $Formula: (10 \mid f(10))$ $Formula: (10 \mid f(10))$ und zeichne für $Formula: x \geq 10$ $Formula: x \geq 10$ in Abbildung 1 ein.

(zur Kontrolle: Gleichung von $Formula: \small{t: y = -0,12x + 3}$ $Formula: \small{t: y = -0,12x + 3}$ )

4 BE

Betrachtet wird die Schar der in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierten Funktionen $Formula: g_k : x \mapsto 3x\cdot\mathrm e^{kx}$ $Formula: g_k : x \mapsto 3x\cdot\mathrm e^{kx}$ mit $Formula: k \in \mathbb{R} \setminus \{0\}.$ $Formula: k \in \mathbb{R} \setminus \{0\}.$ Der Graph jeder Funktion der Schar hat genau einen Extrempunkt Formula: E_k. Abbildung 2 zeigt den Graphen einer Funktion dieser Schar.

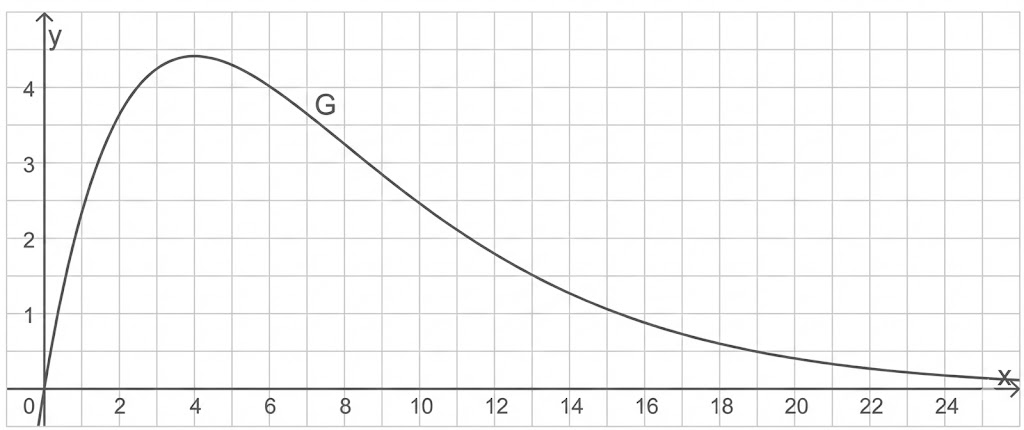
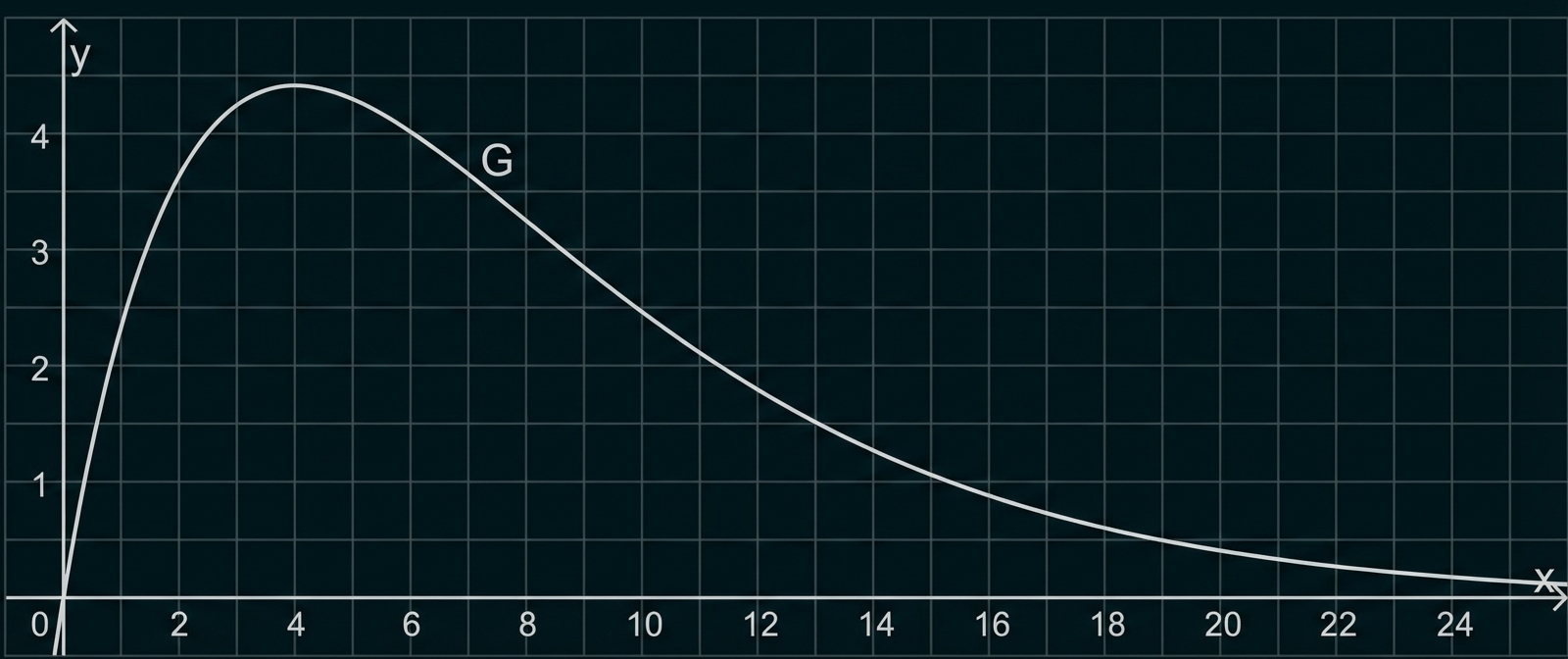
Koordinatensystem mit Kurve G, Maximum bei x≈3 y≈4,5, fällt dann langsam und nähert sich 0 für große x

Abb. 2

Alle Extrempunkte Formula: E_k liegen auf der Gerade Formula: h. Bestimme rechnerisch die Steigung von

5 BE

Der Graph Formula: G besitzt den Hochpunkt $Formula: \left(4\,\bigg\vert\,\dfrac{12}{\mathrm e}\right).$ $Formula: \left(4\,\bigg\vert\,\dfrac{12}{\mathrm e}\right).$

Begründe, dass Formula: G der Graph der Funktion Formula: g_k mit Formula: k = −0,25 ist.

2 BE

Gib alle Werte $Formula: a \in \mathbb{R}$ $Formula: a \in \mathbb{R}$ an, für die die Gleichung $Formula: 3\mathrm e^{-0,25x}= a$ $Formula: 3\mathrm e^{-0,25x}= a$ genau eine Lösung besitzt.

2 BE

Junge Hunde wachsen in ihren ersten Lebensmonaten sehr schnell zu ausgewachsenen Hunden heran. Zur Beschreibung der Zunahme der Körpermasse eines Hundes einer bestimmten Rasse in den ersten 25 Lebensmonaten werden die folgenden beiden Modelle betrachtet:

Für Modell wird für $Formula: 0 \leq x \leq 10$ $Formula: 0 \leq x \leq 10$ der Graph aus Aufgabe 1 und für $Formula: 10 \leq x \leq 25$ $Formula: 10 \leq x \leq 25$ die Tangente (vgl. Aufgabe 1c) verwendet.
Für Modell wird für $Formula: 0 \leq x \leq 25$ $Formula: 0 \leq x \leq 25$ der Graph der Funktion $Formula: g_{-0,25}$ $Formula: g_{-0,25}$ aus Aufgabe 2 genutzt.

In beiden Modellen steht die Formula: x -Koordinate des jeweiligen Punkts auf den Graphen bzw. der Tangente für die Zeit in Monaten, die seit der Geburt des Hundes vergangen sind, und seine Formula: y -Koordinate für die momentane Änderungsrate der Körpermasse des Hundes in Kilogramm pro Monat. Dabei wird vereinfachend davon ausgegangen, dass jeder Monat 30 Tage hat.

Formuliere eine Aussage im Sachzusammenhang, die für beide Modelle für Formula: x = 4 zutrifft.

1 BE

Berechne auf der Grundlage von Modell Formula: A, wie viele Monate nach der Geburt ein Hund der betrachteten Rasse erstmals nicht mehr an Körpermasse zunimmt.

(zur Kontrolle: 25 Monate)

2 BE

Begründe, dass auf der Grundlage von Modell Formula: A die Masse in Kilogramm, um die ein Hund der betrachteten Rasse in den ersten 25 Monaten nach seiner Geburt insgesamt zunimmt, mit dem Term $Formula: \displaystyle\int_0^{10}f(x)\;\mathrm dx+13,5$ $Formula: \displaystyle\int_0^{10}f(x)\;\mathrm dx+13,5$ berechnet werden kann.

3 BE

Die Funktionen Formula: f und $Formula: g_{-0,25},$ $Formula: g_{-0,25},$ die für die Modelle Formula: A bzw. Formula: B verwendet werden, stimmen im Bereich $Formula: 0 \leq x \leq 10$ $Formula: 0 \leq x \leq 10$ nur für Formula: x = 0 in ihren Funktionswerten überein. Zur Entwicklung weiterer Modelle sind in Formula: [0;10] definierte Funktionen gesucht, deren Funktionswerte für $Formula: x \gt 0$ $Formula: x \gt 0$ zwischen den Funktionswerten von Formula: f und $Formula: g_{-0,25}$ $Formula: g_{-0,25}$ liegen. Gib für zwei verschiedene solche Funktionen jeweils einen Funktionsterm an.

4 BE

30 BE

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Der Graph der ganzrationalen Funktion Formula: f ist nicht symmetrisch bezüglich des Koordinatenursprungs, da der Term von nicht nur Potenzen von Formula: x mit ungeradem Exponenten enthält. Für die ersten beiden Ableitungen von ergibt sich:

$Formula: f'(x)=\dfrac{1}{100} \cdot\left(6 x^2-86 x+248\right)$ $Formula: f'(x)=\dfrac{1}{100} \cdot\left(6 x^2-86 x+248\right)$

$Formula: f''(x)=\dfrac{1}{100} \cdot(12 x-86)$ $Formula: f''(x)=\dfrac{1}{100} \cdot(12 x-86)$

Für $Formula: x\lt7 \frac{1}{6}$ $Formula: x\lt7 \frac{1}{6}$ gilt $Formula: 12x\lt86$ $Formula: 12x\lt86$ und somit $Formula: f''(x)\lt0.$ $Formula: f''(x)\lt0.$

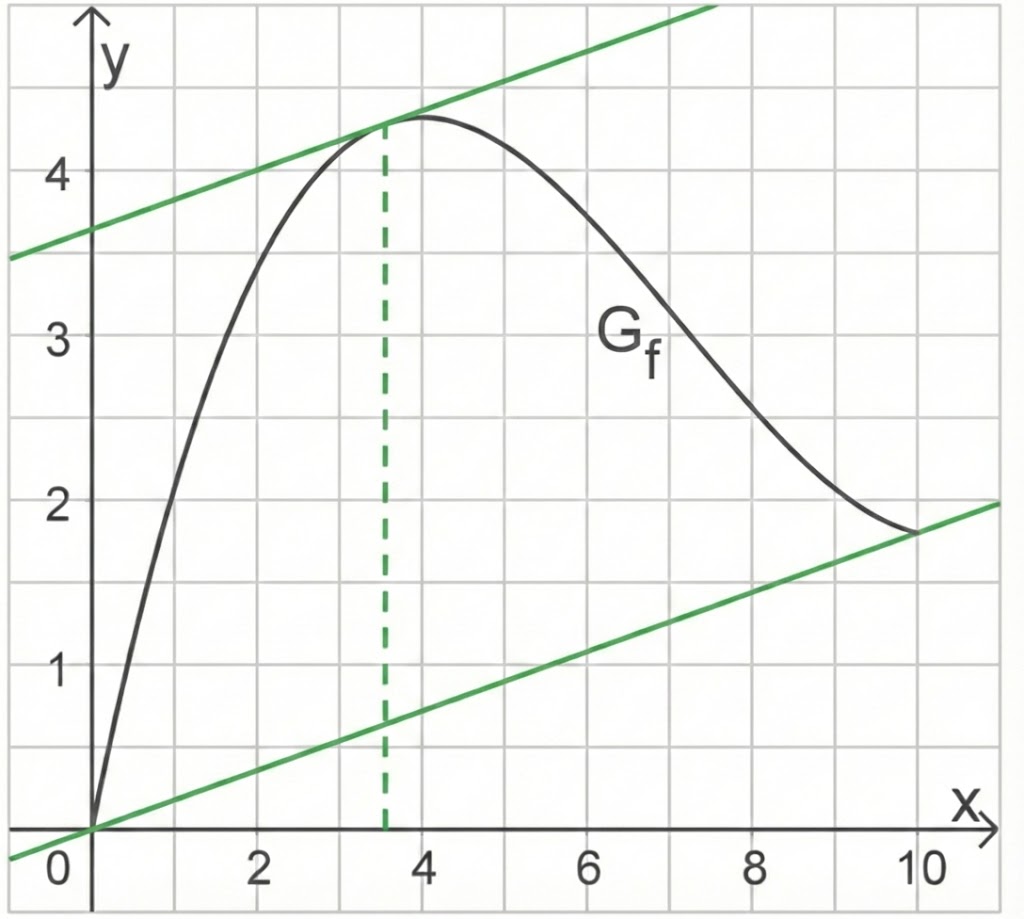
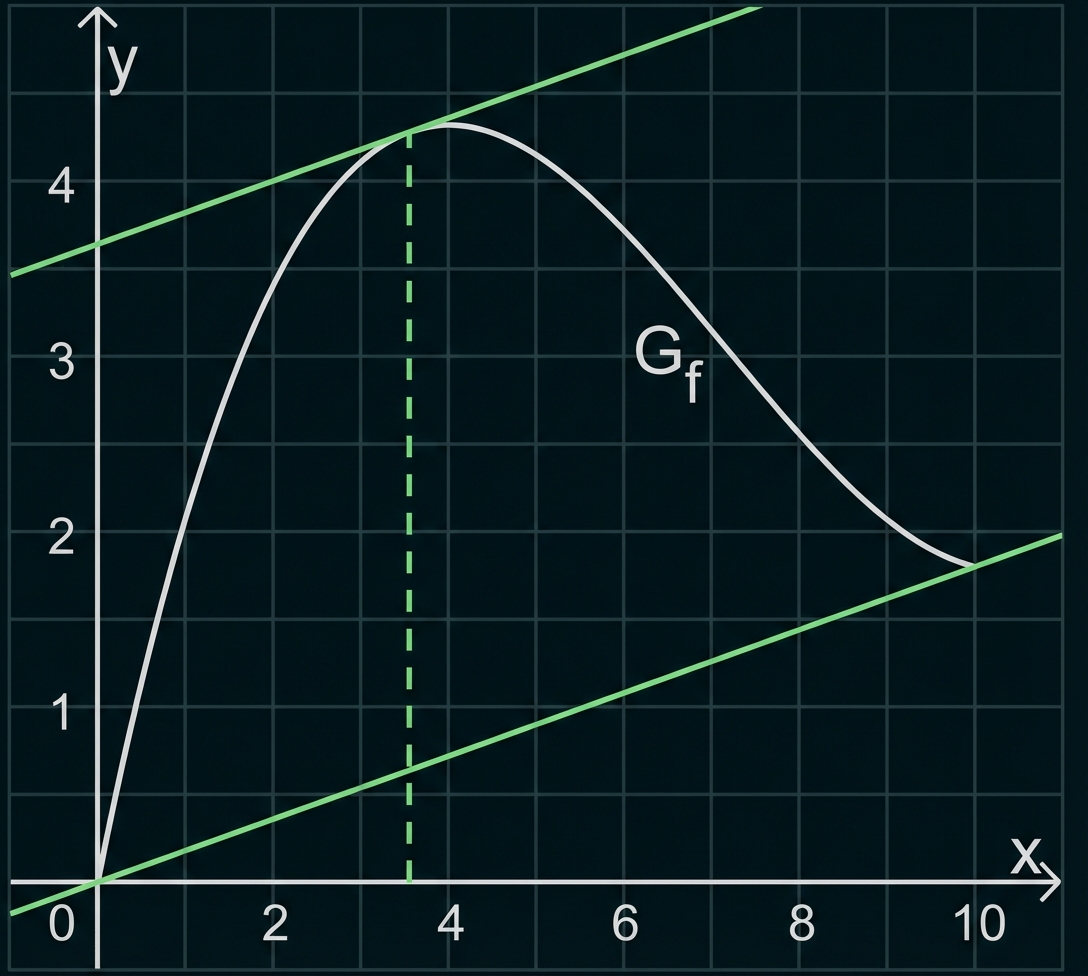
Graphische Bestimmung der lokalen Steigung des Graphen von f

Aus der Abbildung folgt $Formula: x_0\approx3,6.$ $Formula: x_0\approx3,6.$

$Formula: \begin{array}[t]{rll} f'(10)&=& -0,12 \\[5pt] f(10) &=& 1,8 \end{array}$ $Formula: \begin{array}[t]{rll} f'(10)&=& -0,12 \\[5pt] f(10) &=& 1,8 \end{array}$

Einsetzen der Steigung und der Koordinaten des Punktes in die allgemeine Tangentengleichung liefert:

$Formula: \begin{array}[t]{rll}1,8&=&-0,12 \cdot 10+n &\quad\mid\;+1,2 \\[5pt] 3 &=& n \end{array}$ $Formula: \begin{array}[t]{rll}1,8&=&-0,12 \cdot 10+n &\quad\mid\;+1,2 \\[5pt] 3 &=& n \end{array}$

Somit ist Formula: y=-0,12 x+3 eine mögliche Gleichung der Tangente.

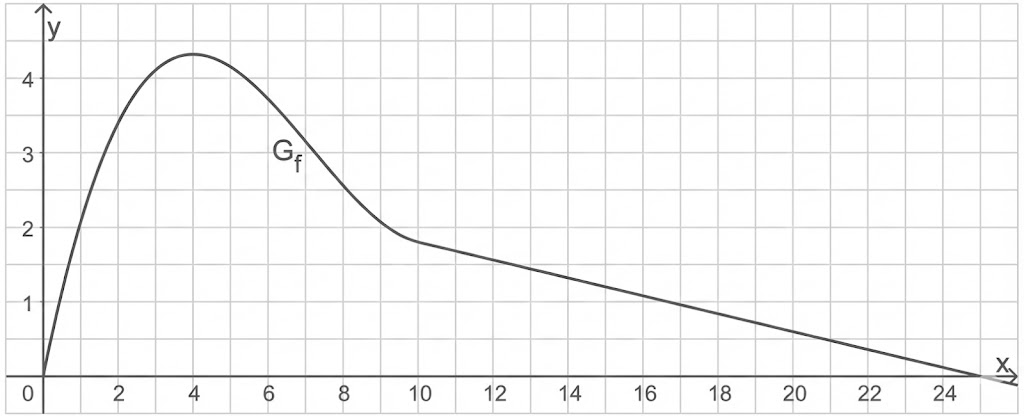
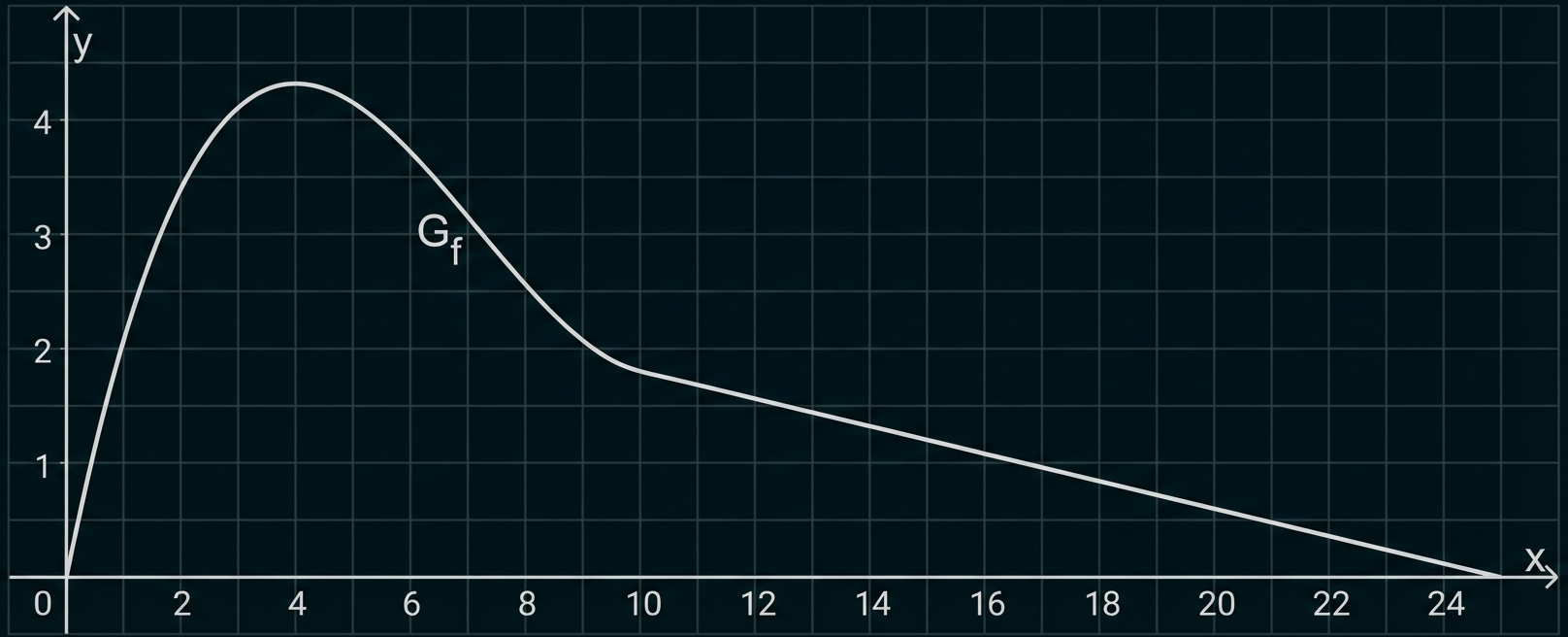
Koordinatensystem mit Funktion G_f, steigt bis etwa x=3 (y≈4,5), fällt danach und geht linear gegen y=0 bei x≈24.

$Formula: g_k'(x)=3 \cdot \mathrm e^{k x}+3 x \cdot k \cdot \mathrm e^{k x}$ $Formula: g_k'(x)=3 \cdot \mathrm e^{k x}+3 x \cdot k \cdot \mathrm e^{k x}$ $Formula: =3 \mathrm e^{k x} \cdot(1+k x)$ $Formula: =3 \mathrm e^{k x} \cdot(1+k x)$

Da die $Formula: \mathrm e$ $Formula: \mathrm e$ -Funktion stets ungleich Null ist, liefert Nullsetzen der Ableitung:

$Formula: \begin{array}[t]{rll} g_k'(x)&=&0 \\[5pt] 1+k x&=&0 &\quad\mid\;-1\\[5pt] k x&=&-1 &\quad\mid\;:k \\[5pt] x &=& -\dfrac{1}{k} \end{array}$ $Formula: \begin{array}[t]{rll} g_k'(x)&=&0 \\[5pt] 1+k x&=&0 &\quad\mid\;-1\\[5pt] k x&=&-1 &\quad\mid\;:k \\[5pt] x &=& -\dfrac{1}{k} \end{array}$

$Formula: g_k^{\prime}(x)=0 \Leftrightarrow x=-\frac{1}{k}$

Mit $Formula: E_1\left(-1 \mid-3 \mathrm e^{-1}\right)$ $Formula: E_1\left(-1 \mid-3 \mathrm e^{-1}\right)$ und $Formula: E_3\left(\left.-\frac{1}{3} \right\rvert\,-\mathrm e^{-1}\right)$ $Formula: E_3\left(\left.-\frac{1}{3} \right\rvert\,-\mathrm e^{-1}\right)$ ergibt sich für die Steigung der Gerade:

$Formula: \dfrac{-\mathrm e^{-1}-\left(-3 \mathrm e^{-1}\right)}{-\frac{1}{3}-(-1)}=\frac{2 \mathrm e^{-1}}{\frac{2}{3}}=3 \mathrm e^{-1}$ $Formula: \dfrac{-\mathrm e^{-1}-\left(-3 \mathrm e^{-1}\right)}{-\frac{1}{3}-(-1)}=\frac{2 \mathrm e^{-1}}{\frac{2}{3}}=3 \mathrm e^{-1}$

$Formula: \begin{array}[t]{rll} g_k(4)&=&\dfrac{12}{\mathrm e} \\[5pt] 12 \cdot \mathrm e^{4 k}&=&\dfrac{12}{\mathrm e} &\quad\mid\;:12 \\[5pt] \mathrm e^{4 k}&=&\dfrac{1}{\mathrm e} &\quad\mid\;\ln \\[5pt] 4k&=&\ln(1)-\ln(\mathrm e) &\quad\mid\;:4 \\[5pt] k &=&-0,25 \end{array}$ $Formula: \begin{array}[t]{rll} g_k(4)&=&\dfrac{12}{\mathrm e} \\[5pt] 12 \cdot \mathrm e^{4 k}&=&\dfrac{12}{\mathrm e} &\quad\mid\;:12 \\[5pt] \mathrm e^{4 k}&=&\dfrac{1}{\mathrm e} &\quad\mid\;\ln \\[5pt] 4k&=&\ln(1)-\ln(\mathrm e) &\quad\mid\;:4 \\[5pt] k &=&-0,25 \end{array}$

$Formula: a=\frac{12}{\mathrm{e}}$ $Formula: a=\frac{12}{\mathrm{e}}$ oder $Formula: a \in\;]-\infty ; 0]$ $Formula: a \in\;]-\infty ; 0]$

Vier Monate nach der Geburt nimmt die Masse eines Hundes der betrachteten Rasse am stärksten zu.

$Formula: \begin{array}[t]{rll} -0,12 x+3&=&0 &\quad\mid\;-3\\[5pt] -0,12 x&=&-3 &\quad\mid\;:(-0,12)\\[5pt] x&=&25 \end{array}$ $Formula: \begin{array}[t]{rll} -0,12 x+3&=&0 &\quad\mid\;-3\\[5pt] -0,12 x&=&-3 &\quad\mid\;:(-0,12)\\[5pt] x&=&25 \end{array}$

Der Graph Formula: G_f für $Formula: 0 \leq x \leq 10$ $Formula: 0 \leq x \leq 10$ und die Tangente Formula: t für $Formula: 10 \leq x \leq 25$ $Formula: 10 \leq x \leq 25$ beschreiben die lokale Änderungsrate der Zunahme der Körpermasse. Die Zunahme der Körpermasse in den ersten 25 Lebensmonaten ist die zu dieser lokalen Änderungsrate gehörige Gesamtänderung. Sie lässt sich folglich mithilfe der Summe aus dem Inhalt des Flächenstücks, das im Bereich $Formula: 0 \leq x \leq 10$ $Formula: 0 \leq x \leq 10$ von Formula: G_f und der Formula: x -Achse begrenzt wird, und dem Flächeninhalt des Dreiecks, das im Bereich $Formula: 10 \leq x \leq 25$ $Formula: 10 \leq x \leq 25$ von der Tangente Formula: t und der -Achse begrenzt wird, ermitteln.

$Formula: \dfrac{1}{2} \cdot\left(f(x)+g_{-0,25}(x)\right)$ $Formula: \dfrac{1}{2} \cdot\left(f(x)+g_{-0,25}(x)\right)$

$Formula: \dfrac{1}{4} \cdot f(x)+\dfrac{3}{4} \cdot g_{-0,25}(x)$ $Formula: \dfrac{1}{4} \cdot f(x)+\dfrac{3}{4} \cdot g_{-0,25}(x)$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?