B2 – Analysis

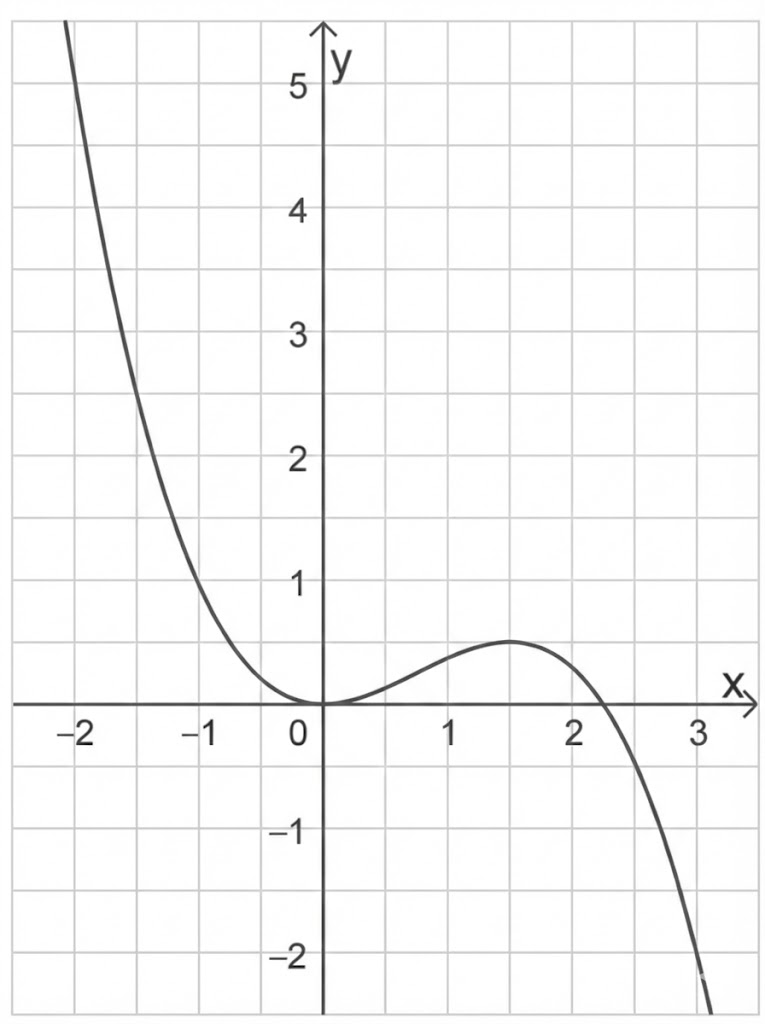
Gegeben ist die in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierte Funktion $Formula: f: x \mapsto-\tfrac{8}{27} x^3+ax^2$ $Formula: f: x \mapsto-\tfrac{8}{27} x^3+ax^2$ mit $Formula: a \in \mathbb{R}.$ $Formula: a \in \mathbb{R}.$ Die Nullstellen von sind Formula: 0 und $Formula: \tfrac{9}{4}.$ $Formula: \tfrac{9}{4}.$ Abbildung 1 zeigt den Graphen Formula: G_f von Formula: f.

Bestimme rechnerisch den Wert von Formula: a.

(zur Kontrolle: $Formula: \small{a=\tfrac{2}{3}}$ $Formula: \small{a=\tfrac{2}{3}}$ )

2 BE

Berechne den Inhalt des Flächenstücks, das Formula: G_f im ersten Quadranten mit der Formula: x -Achse einschließt.

3 BE

Die Tangente an Formula: G_f im Punkt $Formula: \left(\left.\dfrac{9}{4}\,\right\rvert\, 0\right)$ $Formula: \left(\left.\dfrac{9}{4}\,\right\rvert\, 0\right)$ wird mit Formula: t bezeichnet.

Weise nach, dass Formula: t durch den Punkt $Formula: \left(0\,\left\lvert\, \tfrac{27}{8}\right.\right)$ $Formula: \left(0\,\left\lvert\, \tfrac{27}{8}\right.\right)$ verläuft. Begründe, dass der Inhalt des Flächenstücks, das Formula: G_f im ersten Quadranten mit und der Formula: y -Achse einschließt, kleiner als $Formula: \tfrac{1}{2} \cdot \tfrac{9}{4} \cdot \tfrac{27}{8}$ $Formula: \tfrac{1}{2} \cdot \tfrac{9}{4} \cdot \tfrac{27}{8}$ ist.

5 BE

Koordinatensystem mit Gitternetz und einer geschwungenen Kurve, die über und unter der x-Achse verläuft.

Eine in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierte ganzrationale Funktion Formula: g hat die folgenden Eigenschaften:

ist Tangente an den Graphen von im Punkt $Formula: \left(\left.\tfrac{9}{4}\,\right\rvert\, 0\right).$ $Formula: \left(\left.\tfrac{9}{4}\,\right\rvert\, 0\right).$
Der Graph von verläuft für $Formula: 0\lt x\lt\tfrac{9}{4}$ $Formula: 0\lt x\lt\tfrac{9}{4}$ oberhalb von

Gib einen möglichen Term von Formula: g an.

3 BE

In einer Messstation wird seit 1958 kontinuierlich die CO₂-Konzentration in der Luft gemessen, die in ppm (parts per million) angegeben wird. Die Tabelle gibt für die Jahre 1960, 1985 und 2010 jeweils den jährlichen Durchschnittswert der Messwerte an.

Jahr	1960	1985	2010
CO₂-Konzentration	$Formula: 317\;\text{ppm}$ $Formula: 317\;\text{ppm}$	$Formula: 346\;\text{ppm}$ $Formula: 346\;\text{ppm}$	$Formula: 390\;\text{ppm}$ $Formula: 390\;\text{ppm}$

Die jährlichen Durchschnittswerte haben sich im Zeitraum von 1960 bis 1985 in guter Näherung exponentiell entwickelt. Ermittle die zugehörige Wachstumsrate in Prozent.

(zur Kontrolle: etwa $Formula: \small{0,35\,\%}$ $Formula: \small{0,35\,\%}$ )

3 BE

Berechne unter der Annahme, dass sich das exponentielle Wachstum nach 1985 in gleicher Weise fortgesetzt hat, den jährlichen Durchschnittswert für das Jahr 2010. Vergleiche diesen Wert mit dem zugehörigen Wert aus der Tabelle und formuliere das Ergebnis deines Vergleichs im Sachzusammenhang.

3 BE

Innerhalb eines Jahres schwankt die CO₂-Konzentration. Für einen bestimmten Zeitraum von acht Monaten lassen sich die gemessenen Werte modellhaft durch die in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierte Funktion $Formula: k: x \mapsto 3,3 \cdot \sin \left(\tfrac{\pi}{6} x\right)+406$ $Formula: k: x \mapsto 3,3 \cdot \sin \left(\tfrac{\pi}{6} x\right)+406$ beschreiben. Dabei ist Formula: x die in diesem Zeitraum vergangene Zeit in Monaten und Formula: k(x) die CO₂-Konzentration in ppm. Vereinfachend wird davon ausgegangen, dass jeder Monat 30 Tage hat.

Gib an, wie der Graph von Formula: k schrittweise aus dem Graphen der in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierten Funktion $Formula: s: x \mapsto \sin (x)$ $Formula: s: x \mapsto \sin (x)$ hervorgeht. Beurteile, ob die Reihenfolge der einzelnen Schritte von Bedeutung ist.

5 BE

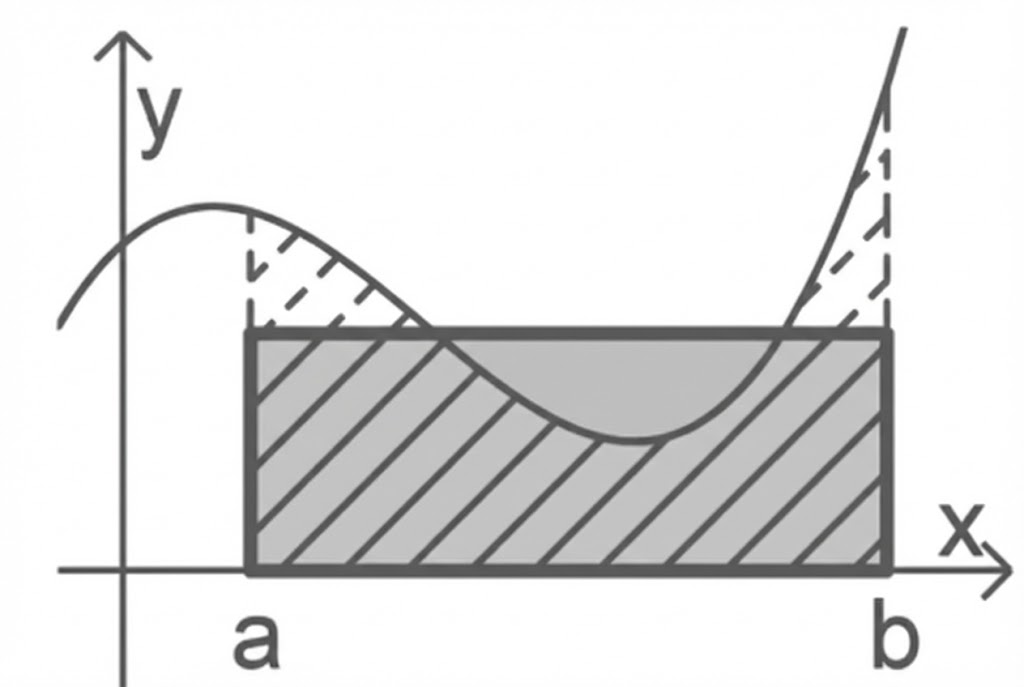
Der durchschnittliche Funktionswert einer Funktion Formula: h im Intervall Formula: [a ; b] kann mithilfe der folgenden Überlegung bestimmt werden:

Schließt der Graph von Formula: h mit der Formula: x -Achse und den Geraden mit den Gleichungen und ein Flächenstück ein, so gibt es ein Rechteck der Länge Formula: b-a, das den gleichen Flächeninhalt wie das Flächenstück hat (vgl. Abbildung 2). Die Breite dieses Rechtecks stimmt mit dem Betrag des durchschnittlichen Funktionswerts von im Intervall überein.

Koordinatensystem mit schraffiertem Rechteck zwischen x=a und x=b und einer geschwungenen Kurve darüber

Bestimme für den betrachteten Zeitraum von acht Monaten die prozentuale Abweichung des Maximums der CO₂-Konzentration von der durchschnittlichen CO₂-Konzentration.

6 BE

30 BE

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$Formula: \begin{array}[t]{rll}f\left(\dfrac{9}{4}\right)&=&0 \\[5pt] -\dfrac{8}{27} \cdot\left(\dfrac{9}{4}\right)^3+a \cdot\left(\dfrac{9}{4}\right)^2&=&0 &\quad\mid\;\cdot\left(\frac{4}{9}\right)^2 \\[5pt] -\dfrac{8}{27} \cdot\dfrac{9}{4}+a &=&0 &\quad\mid\;+\frac{2}{3} \\[5pt] a &=& \dfrac{2}{3} \end{array}$ $Formula: \begin{array}[t]{rll}f\left(\dfrac{9}{4}\right)&=&0 \\[5pt] -\dfrac{8}{27} \cdot\left(\dfrac{9}{4}\right)^3+a \cdot\left(\dfrac{9}{4}\right)^2&=&0 &\quad\mid\;\cdot\left(\frac{4}{9}\right)^2 \\[5pt] -\dfrac{8}{27} \cdot\dfrac{9}{4}+a &=&0 &\quad\mid\;+\frac{2}{3} \\[5pt] a &=& \dfrac{2}{3} \end{array}$

$Formula: \begin{array}[t]{rll}A&=&\displaystyle\int_0^{\tfrac{9}{4}} f(x)\;\mathrm d x \\[5pt] &=&\left[-\dfrac{2}{27} x^4+\dfrac{2}{9} x^3\right]_0^{\tfrac{9}{4}} \\[5pt] &=&-\dfrac{2}{27} \cdot\left(\dfrac{9}{4}\right)^4+\dfrac{2}{9} \cdot\left(\dfrac{9}{4}\right)^3 \\[5pt] &=& \dfrac{81}{128} \end{array}$ $Formula: \begin{array}[t]{rll}A&=&\displaystyle\int_0^{\tfrac{9}{4}} f(x)\;\mathrm d x \\[5pt] &=&\left[-\dfrac{2}{27} x^4+\dfrac{2}{9} x^3\right]_0^{\tfrac{9}{4}} \\[5pt] &=&-\dfrac{2}{27} \cdot\left(\dfrac{9}{4}\right)^4+\dfrac{2}{9} \cdot\left(\dfrac{9}{4}\right)^3 \\[5pt] &=& \dfrac{81}{128} \end{array}$

$Formula: f'(x)=-\dfrac{8}{9} x^2+\dfrac{4}{3} x$ $Formula: f'(x)=-\dfrac{8}{9} x^2+\dfrac{4}{3} x$

Für die Steigung im Punkt an den die Tangente anliegt folgt:

$Formula: f'\left(\dfrac{9}{4}\right)=-\dfrac{3}{2}$ $Formula: f'\left(\dfrac{9}{4}\right)=-\dfrac{3}{2}$

Einsetzen der Koordinaten des Punktes und der Steigung in die allgemeine Tangentengleichung liefert:

$Formula: \begin{array}[t]{rll}0&=&-\dfrac{3}{2} \cdot \dfrac{9}{4}+n &\quad\mid\;+\frac{27}{8}\\[5pt] \dfrac{27}{8} &=& n \end{array}$ $Formula: \begin{array}[t]{rll}0&=&-\dfrac{3}{2} \cdot \dfrac{9}{4}+n &\quad\mid\;+\frac{27}{8}\\[5pt] \dfrac{27}{8} &=& n \end{array}$

Somit verläuft Formula: t durch den Punkt aus der Aufgabenstellung.

Der in der Aufgabenstellung angegebene Term gibt den Flächeninhalt des Dreiecks an, das die Koordinatenachsen mit der Tangente einschließen. Für $Formula: 0\lt x\lt\tfrac{9}{4}$ $Formula: 0\lt x\lt\tfrac{9}{4}$ verläuft Formula: G_f innerhalb dieses Dreiecks.

$Formula: g(x)=-\dfrac{3}{2} x+\dfrac{27}{8}+\left(x-\dfrac{9}{4}\right)^2$ $Formula: g(x)=-\dfrac{3}{2} x+\dfrac{27}{8}+\left(x-\dfrac{9}{4}\right)^2$

$Formula: \begin{array}[t]{rll}317 \cdot p^{25}&=&346 &\quad\mid\;:317\\[5pt] p^{25}&=&\dfrac{346}{317} &\quad\mid\;\sqrt[25]{\;}\\[5pt] p &=& \sqrt[25]{\dfrac{346}{317}} \end{array}$ $Formula: \begin{array}[t]{rll}317 \cdot p^{25}&=&346 &\quad\mid\;:317\\[5pt] p^{25}&=&\dfrac{346}{317} &\quad\mid\;\sqrt[25]{\;}\\[5pt] p &=& \sqrt[25]{\dfrac{346}{317}} \end{array}$

Es gilt $Formula: \sqrt[25]{\tfrac{346}{317}} \approx 1,0035,$ $Formula: \sqrt[25]{\tfrac{346}{317}} \approx 1,0035,$ d. h. die jährliche Wachstumsrate beträgt etwa $Formula: 0,35\,\%.$ $Formula: 0,35\,\%.$

$Formula: 346 \cdot 1,0035^{25} \approx 378\lt390$ $Formula: 346 \cdot 1,0035^{25} \approx 378\lt390$

Der Durchschnittswert der CO₂-Konzentration für das Jahr 2010 ist somit größer als der, der sich bei einer unveränderten Fortsetzung des exponentiellen Wachstums ergeben hätte.

Der Graph von Formula: k geht aus dem Graphen von Formula: s hervor durch

Streckung in -Richtung mit dem Faktor $Formula: \tfrac{6}{\pi}$ $Formula: \tfrac{6}{\pi}$
Streckung in -Richtung mit dem Faktor
Verschiebung um in positive -Richtung

Die Reihenfolge der Schritte ist von Bedeutung. Würde die Verschiebung in Formula: y -Richtung vor der Streckung in -Richtung durchgeführt werden, so hätten die Punkte des entstehenden Graphen deutlich größere -Koordinaten als die des Graphen von $k.$

$Formula: \begin{array}[t]{rll}A&=&\dfrac{1}{8} \cdot \displaystyle\int_0^8 k(x)\;\mathrm dx \\[5pt] &=&\dfrac{1}{8} \cdot\left[-\dfrac{3,3 \cdot 6}{\pi} \cdot \cos \left(\dfrac{\pi}{6} x\right)+406 x\right]_0^8 \\[5pt] &\approx& 407,2 \end{array}$ $Formula: \begin{array}[t]{rll}A&=&\dfrac{1}{8} \cdot \displaystyle\int_0^8 k(x)\;\mathrm dx \\[5pt] &=&\dfrac{1}{8} \cdot\left[-\dfrac{3,3 \cdot 6}{\pi} \cdot \cos \left(\dfrac{\pi}{6} x\right)+406 x\right]_0^8 \\[5pt] &\approx& 407,2 \end{array}$

Für die prozentuale Abweichung folgt damit:

$Formula: \dfrac{k(3)-407,2}{407,2}=\dfrac{409,3-407,2}{407,2}$ $Formula: \dfrac{k(3)-407,2}{407,2}=\dfrac{409,3-407,2}{407,2}$ $Formula: \approx 0,5\,\%$ $Formula: \approx 0,5\,\%$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?