B5 – Geometrie
Gegeben sind die Punkte 
und 
Es gilt 
somit ist das Viereck 
ein Trapez.
Zeige, dass das Trapez bei 
einen rechten Innenwinkel hat.
Bestimme den Flächeninhalt des Trapezes 
(zur Kontrolle: 
)
Das Trapez liegt in der Ebene 
Bestimme eine Gleichung von 
in Koordinatenform.
(zur Kontrolle: 
)
In einem Modell stellt die 
-Ebene die horizontale Grundfläche dar, auf der sich ein Hügel erhebt. Ein Hang des Hügels wird durch das Trapez dargestellt. Auf einem parallel zur Grundfläche verlaufenden Plateau, das durch ein Viereck mit 
und als Eckpunkten beschrieben wird, steht eine Burg. Die höchste Stelle der vorderen Fassade der Burg wird dabei durch den Punkt 
dargestellt (vgl. Abbildung). Eine Längeneinheit entspricht 
in der Realität.
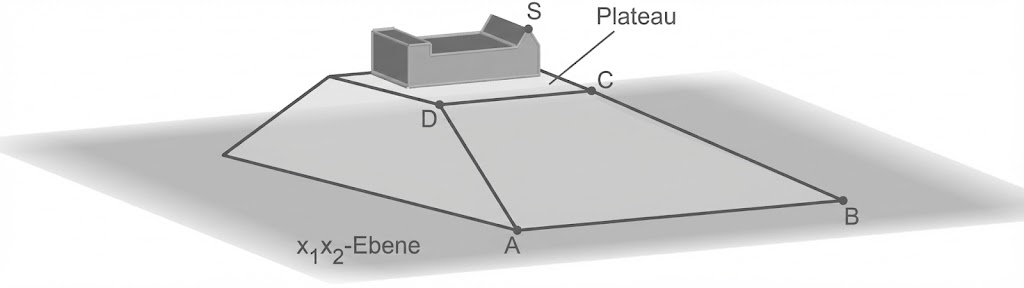
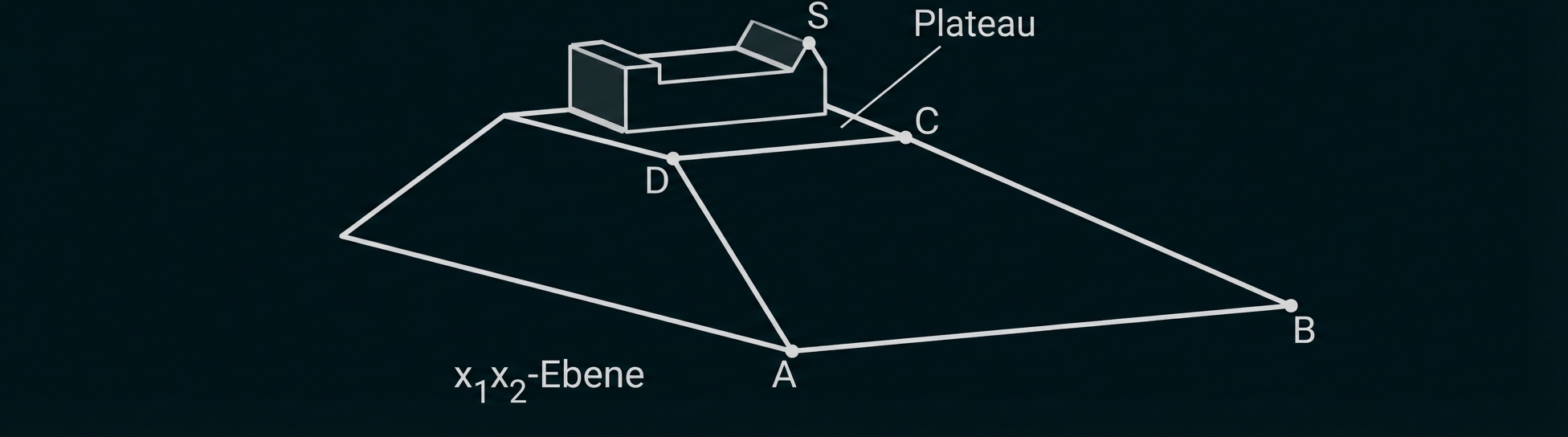
Bestimme die Höhe der vorderen Burgfassade an ihrer höchsten Stelle in Metern.
Der durch das Trapez beschriebene Hang wird auf seiner gesamten Fläche für den Weinanbau genutzt. Berechne den Inhalt der Weinanbaufläche des Hangs in Hektar und untersuche mithilfe der folgenden Tabelle, um welche Art von Weinanbaulage es sich handelt.
|
Art der Wein- anbaulage |
Größe des Neigungswinkels des Hangs gegenüber der horizontalen Grundfläche |
|---|---|
|
Flachlage |
|
|
Hanglage |
|
|
Steillage |
|
Bei der Weinlese steht ein Arbeiter auf dem Hang an einer Stelle, die durch den Punkt 
beschrieben wird. Er stellt sich dort auf seine Zehenspitzen und versucht, aus einer Blickhöhe von zwei Metern die Burg zu sehen. Beurteile, ob der Hang dabei die freie Sicht auf die höchste Stelle der vorderen Fassade der Burg verhindert.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
![Formula: \begin{array}[t]{rll} \overrightarrow{A B} \times \overrightarrow{A D}&=&\left(\begin{array}{c}0 \\ 30 \\ 0\end{array}\right) \times\left(\begin{array}{c}-15 \\ 0 \\ 8\end{array}\right) \\[5pt] &=&\left(\begin{array}{c}240 \\ 0 \\ 450\end{array}\right) \\[5pt] &=& 30 \cdot\left(\begin{array}{c}8 \\ 0 \\ 15\end{array}\right) \end{array}](https://www.schullv.de/resources/formulas/ab4b3864b646ca3c404388a3c276cf8a6431bb9d14423de1215ecc0824638247_light.svg)
![Formula: \begin{array}[t]{rll} \overrightarrow{A B} \times \overrightarrow{A D}&=&\left(\begin{array}{c}0 \\ 30 \\ 0\end{array}\right) \times\left(\begin{array}{c}-15 \\ 0 \\ 8\end{array}\right) \\[5pt] &=&\left(\begin{array}{c}240 \\ 0 \\ 450\end{array}\right) \\[5pt] &=& 30 \cdot\left(\begin{array}{c}8 \\ 0 \\ 15\end{array}\right) \end{array}](https://www.schullv.de/resources/formulas/ab4b3864b646ca3c404388a3c276cf8a6431bb9d14423de1215ecc0824638247_dark.svg)
Für eine allgemeine Ebenengleichung folgt somit 
Einsetzen der Koordinaten von 
liefert:
![Formula: \begin{array}[t]{rll} 8\cdot17+15\cdot0-c&=&0 &\quad\mid\;+c\\[5pt] 136 &=& c \end{array}](https://www.schullv.de/resources/formulas/8373b5cb3ad2d785506c86177b95c5adecb016e3febea614af8aec30f4c08e13_light.svg)
![Formula: \begin{array}[t]{rll} 8\cdot17+15\cdot0-c&=&0 &\quad\mid\;+c\\[5pt] 136 &=& c \end{array}](https://www.schullv.de/resources/formulas/8373b5cb3ad2d785506c86177b95c5adecb016e3febea614af8aec30f4c08e13_dark.svg)
Damit ergibt sich 
Inhalt der Anbaufläche: 
Wird die Größe des Neigungswinkels des Hangs mit 
bezeichnet, so gilt:
![Formula: \begin{array}[t]{rll} \cos \varphi&=&\dfrac{\pmatrix{8 \\ 0 \\ 15}\circ\pmatrix{0 \\ 0 \\ 1}}{\left\vert\pmatrix{8 \\ 0 \\ 15}\right\vert\cdot\left\vert\pmatrix{0 \\ 0 \\ 1}\right\vert} \\[5pt] \cos \varphi &=&\dfrac{15}{17} \\[5pt] \varphi &=& \cos^{-1}\left(\dfrac{15}{17}\right) \\[5pt] \varphi &\approx& 28,1^\circ \end{array}](https://www.schullv.de/resources/formulas/eb1c786a503aba211c99e9d510d4be8bf771f8dce4c90f3caf5f60ad7be46865_light.svg)
![Formula: \begin{array}[t]{rll} \cos \varphi&=&\dfrac{\pmatrix{8 \\ 0 \\ 15}\circ\pmatrix{0 \\ 0 \\ 1}}{\left\vert\pmatrix{8 \\ 0 \\ 15}\right\vert\cdot\left\vert\pmatrix{0 \\ 0 \\ 1}\right\vert} \\[5pt] \cos \varphi &=&\dfrac{15}{17} \\[5pt] \varphi &=& \cos^{-1}\left(\dfrac{15}{17}\right) \\[5pt] \varphi &\approx& 28,1^\circ \end{array}](https://www.schullv.de/resources/formulas/eb1c786a503aba211c99e9d510d4be8bf771f8dce4c90f3caf5f60ad7be46865_dark.svg)
Es handelt sich daher um eine Steillage.
Die Blickposition des Arbeiters entspricht dem Punkt 
Für die Gleichung der Gerade durch 
und 
ergibt sich z.B:
Einsetzen in die Gleichung von liefert:
![Formula: \begin{array}[t]{rll} 8 \cdot(-6+11,75 \mu)+15 \cdot(12-5,8 \mu)-136 &=&0 \\[5pt] -4 +7\mu&=&0 &\quad\mid\;+4\\[5pt] 7\mu&=&4 &\quad\mid\;:7\\[5pt] \mu &=& \dfrac{4}{7} \end{array}](https://www.schullv.de/resources/formulas/cbf36dc5c05c90d415ff87fec43c73ff31269a6595085e9b946c98e63d3e373e_light.svg)
![Formula: \begin{array}[t]{rll} 8 \cdot(-6+11,75 \mu)+15 \cdot(12-5,8 \mu)-136 &=&0 \\[5pt] -4 +7\mu&=&0 &\quad\mid\;+4\\[5pt] 7\mu&=&4 &\quad\mid\;:7\\[5pt] \mu &=& \dfrac{4}{7} \end{array}](https://www.schullv.de/resources/formulas/cbf36dc5c05c90d415ff87fec43c73ff31269a6595085e9b946c98e63d3e373e_dark.svg)
Also hat der Schnittpunkt von 
und die 
-Koordinate 
Wegen 
befindet sich dieser oberhalb der Ebene mit der Gleichung 
in welcher die Kante 
liegt. Der Hang verhindert die freie Sicht somit nicht.