Pflichtaufgaben

1 Analysis

Gegeben ist die Funktion $f$ mit $f(x)=x^3+3 x^2, x \in \mathbb{R}.$
$K$ ist der Graph der Funktion.

Berechne

die Koordinaten des Hoch- und des Tiefpunkts von $K$ und
die Steigung von $K$ im Wendepunkt

(5 BE)

2 Analysis

In einem Wassertank wird Wasser gespeichert.
Die Abbildung zeigt den Verlauf der momentanen Änderungsrate $w(t)$ des Wasservolumens im Tank. Dabei ist $t$ die Zeit in Stunden seit Beginn der Beobachtung $(t=0)$ und $w(t)$ die momentane Änderungsrate in $\text{m}^3$ pro Stunde zum Zeitpunkt $t.$ Der Beobachtungszeitraum beträgt $18$ Stunden.

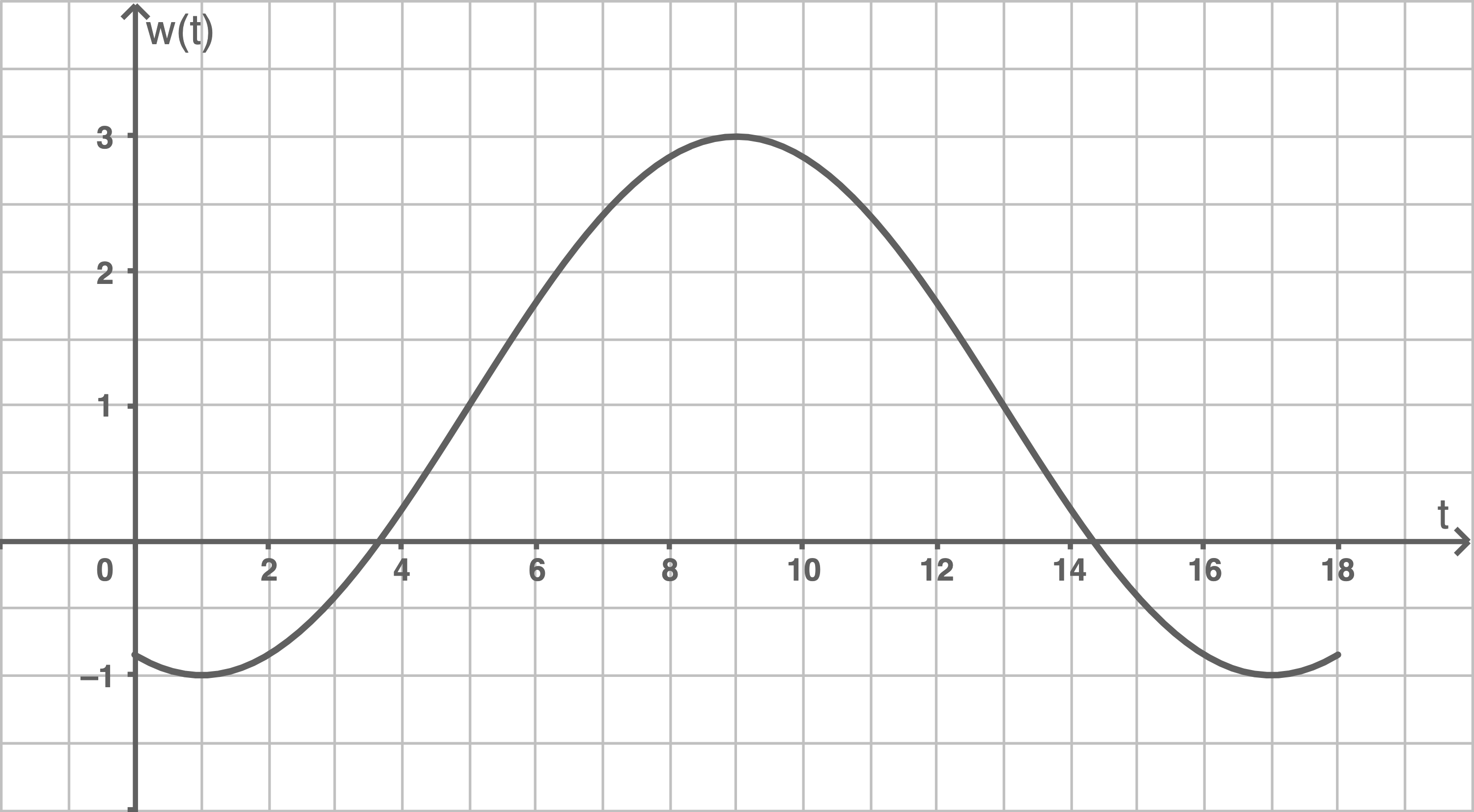
Grafik eines Zeitverlaufs mit einer Wellenform, dargestellt durch eine Kurve auf einem Koordinatensystem.

Begründe, dass neun Stunden nach Beginn der Beobachtung mehr Wasser im Tank ist als zu Beginn.

(2 BE)

Die Funktion $w$ ist eine trigonometrische Funktion.
Ermittle einen möglichen Funktionsterm dieser Funktion.

(3 BE)

3 Stochastik

Die Abbildung zeigt den Graphen der Dichtefunktion einer normalverteilten Zufallsgröße $X.$

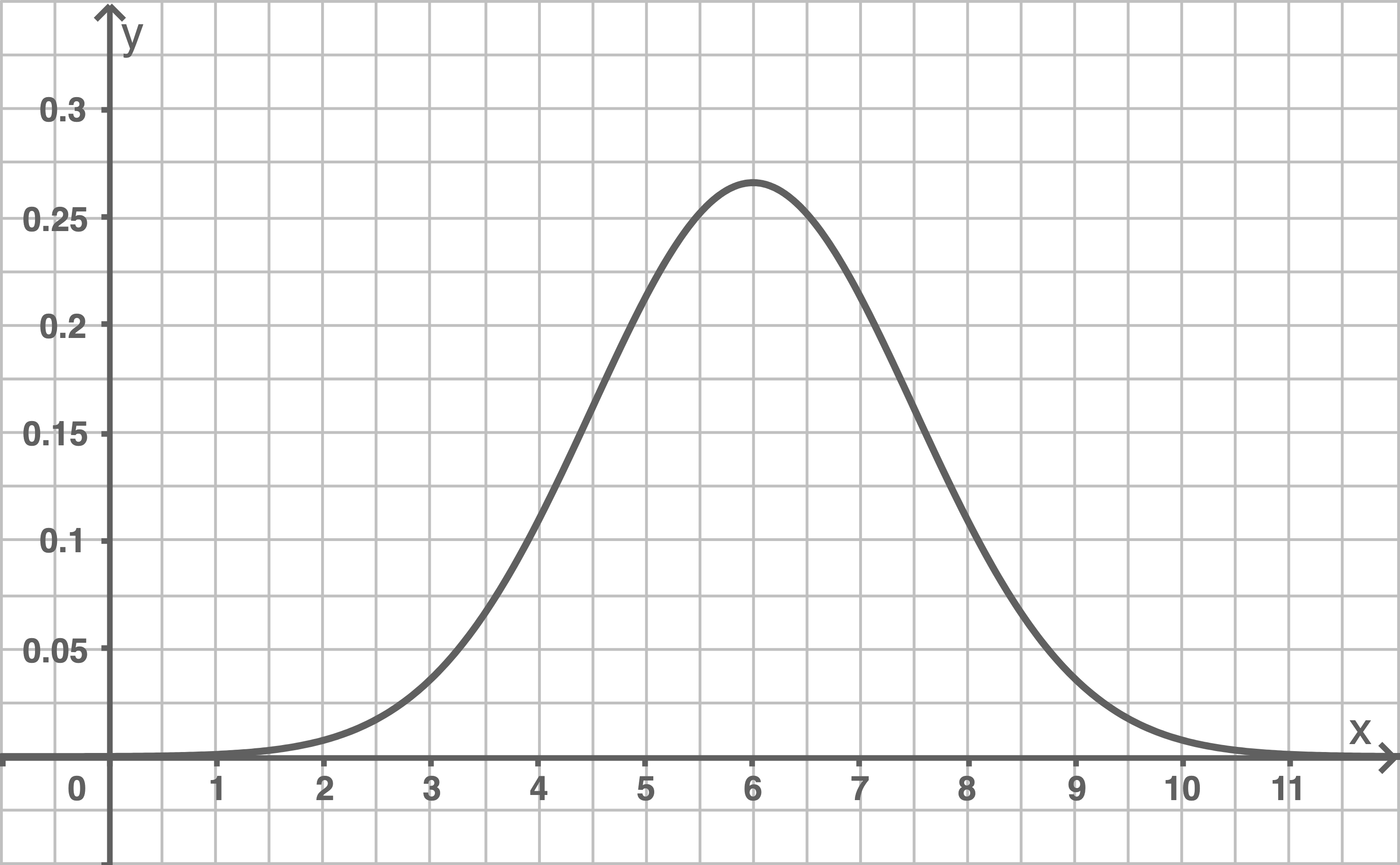
Grafik eines Kurvenverlaufs mit Achsenbeschriftungen x und y.

Gib den Erwartungswert der Zufallsgröße $X$ an.

(1 BE)

Gib näherungsweise den Wert der Standardabweichung von $X$ an.
Begründe diesen.

(2 BE)

Ermittle näherungsweise die Wahrscheinlichkeit, dass der Wert der Zufallsgröße $X$ im Intervall $[5; 7]$ liegt.

(2 BE)

4 Lineare Algebra

Die Punkte $A(5\mid-1\mid 2), B(9\mid2\mid 12)$ und $C(3\mid-2\mid 4)$ sind die Eckpunkte eines Dreiecks $ABC.$

Weise nach, dass das Dreieck $ABC$ bei $C$ einen rechten Winkel besitzt.

(2 BE)

Die abgebildete Skizze stellt das Dreieck $ABC$ dar.

Dreieck mit den Punkten A, B und C, dargestellt in einer einfachen geometrischen Darstellung.

Nun wird ein Punkt $P$ hinzugefügt, sodass dieser zusammen mit $A, B$ und $C$ die Eckpunkte eines Parallelogramms bildet.

Übernehme die Skizze auf dein Lösungsblatt und erweitere diese um einen möglichen Punkt $P.$
Bestimme mögliche Koordinaten des Punktes $P$ so, dass das Parallelogramm kein Rechteck ist.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1 Analysis

Hoch- und Tiefpunkt berechnen

Für die ersten beiden Ableitungen von $f$ folgt:

$\(\begin{array}[t]{rlll} f$

Anwenden der notwendigen Bedingung für Extremstellen $\(f$ ergibt:

$\(\begin{array}[t]{rlll} f$

Mit dem Satz des Nullprodukts folgt somit $x_1=0$ und $3x+6=0,$ d.h. $x_2=-2.$ Überprüfen der hinreichenden Bedingung für Extremstellen liefert:

$\(\begin{array}[t]{rlll} f$

Somit besitzt $K$ bei $x=0$ einen Tiefpunkt und bei $x=-2$ einen Hochpunkt. Für die Funktionswerte ergibt sich:

$\begin{array}[t]{rlll} f(0)&=&0^3+3\cdot0^2 \\[5pt] &=&0 \end{array}$

$\begin{array}[t]{rlll} f(-2)&=&(-2)^3+3\cdot(-2)^2 \\[5pt] &=&-8+12 \\[5pt] &=&4 \end{array}$

Die Koordinaten der beiden Extrempunkte von $K$ sind somit durch $T(0\mid0)$ und $H(-2\mid4)$ gegeben.

Steigung im Wendepunkt berechnen

Für die dritte Ableitung von $f$ folgt:

$\(f$

Anwenden der notwendigen Bedingung für Wendestellen $\(f$ ergibt:

$\(\begin{array}[t]{rlll} f$

Da $\(f$ konstant den Wert $6$ besitzt, ist $x=-1$ somit eine Wendestelle von $f.$ Für die Steigung von $K$ im Wendepunkt folgt somit:

$\(\begin{array}[t]{rlll} f$

2 Analysis

Die Veränderung der Wassermenge im Tank in einem bestimmten Zeitintervall wird durch die Flächenbilanz der Fläche zwischen dem Graphen und der $x$ -Achse in diesem Intervall gegeben.
Mit Hilfe der Abbildung lässt sich erkennen, dass $\displaystyle\int_{0}^{9}w(t)\;\mathrm dt\gt0$ gilt. Somit ist neun Stunden nach Beginn der Beobachtung mehr Wasser im Tank als zu Beginn.

Aus der Abbildung folgt, dass $w$ eine Periodenlänge von $16,$ eine Amplitude von $2$ und einen Hochpunkt bei $(9\mid3)$ besitzt. Damit ist ein möglicher Funktionsterm von $w$ z.B. wie folgt gegeben:

$\begin{array}[t]{rlll} w(t)&=&2\cdot\cos\left(\dfrac{2\pi}{16}\cdot(t-9)\right)+1 \\[5pt] &=&2\cdot\cos\left(\dfrac{\pi}{8}\cdot(t-9)\right)+1 \end{array}$

3 Stochastik

Der Erwartungswert entspricht der Hochstelle der Dichtefunktion und beträgt somit $\mu=6.$

Die Wendestellen der Dichtefunktion können mit Hilfe der Abbildung bei ungefähr $x\approx4,5$ und $x\approx7,5$ abgelesen werden. Damit ergibt sich die Standardabweichung als $\sigma\approx\frac{1}{2}\cdot(7,5-4,5)=1,5.$

Durch Zählen der Kästchen werden im betrachteten Intervall unterhalb des Graphen ungefähr $40$ Koordinatenkästchen erhalten. Diese besitzen jeweils einen Flächeninhalt von $0,025\cdot0,5=0,0125.$ Damit folgt:

$\begin{array}[t]{rlll} P(5\leq X\leq7)&\approx&40\cdot0,0125 \\[5pt] &=&0,5 \\[5pt] &=&50\,\% \end{array}$

4 Lineare Algebra

$\begin{array}[t]{rlll} \overrightarrow{CA}&=&\pmatrix{5\\-1\\2}-\pmatrix{3\\-2\\4} \\[5pt] &=&\pmatrix{2\\1\\-2} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{CB}&=&\pmatrix{9\\2\\12}-\pmatrix{3\\-2\\4} \\[5pt] &=&\pmatrix{6\\4\\8} \end{array}$

Für das Skalarprodukt der beiden Vektoren folgt:

$\begin{array}[t]{rlll} \overrightarrow{CA}\circ\overrightarrow{CB}&=&\pmatrix{2\\1\\-2}\circ\pmatrix{6\\4\\8} \\[5pt] &=&12+4-16 \\[5pt] &=&0 \end{array}$

Somit besitzt das Dreick $ABC$ bei $C$ einen rechten Winkel.

Möglichen Punkt einzeichnen

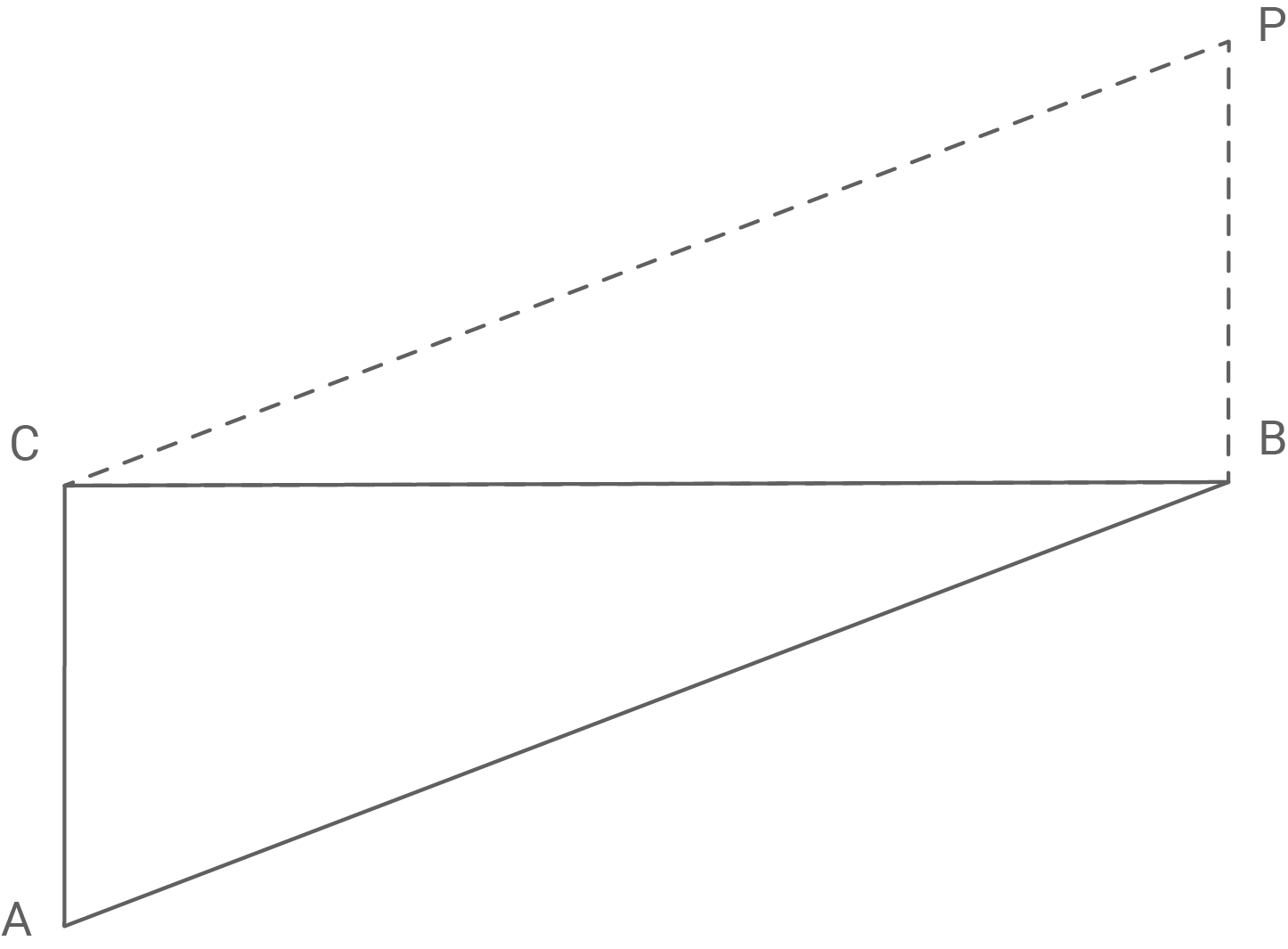
Schematische Darstellung eines rechtwinkligen Dreiecks mit den Punkten A, B, C und einem Punkt P.

Mögliche Koordinaten bestimmen

$\begin{array}[t]{rlll} \overrightarrow{OP}&=&\overrightarrow{OC}+\overrightarrow{AB} \\[5pt] &=&\pmatrix{3\\-2\\4}+\pmatrix{4\\3\\10} \\[5pt] &=&\pmatrix{7\\1\\14} \end{array}$

Mögliche Koordinaten von $P$ sind somit gegeben durch $P(7\mid1\mid14).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?