Stochastik

Aufgabe I 2

An einem Tag kommen durchschnittlich $8500$ Besucher in ein Wintersportgebiet. $20\, \%$ der Besucher können Snowboard fahren.

Berechne, wie viele Besucher des Wintersportgebiets an einem Tag erwartungsgemäß Snowboard fahren können.

(1 BE)

$40\, \%$ der Besucher, die Snowboard fahren können, können auch Ski fahren. $5 \,\%$ aller Besucher können weder Ski noch Snowboard fahren.

Ermittle jeweils die Wahrscheinlichkeit für folgende Ereignisse:

$A:$

„Ein Besucher kann Ski fahren.“

$B:$

„Ein Besucher kann Ski, aber kein Snowboard fahren.“

$C:$

„Ein Besucher, der Ski fahren kann, kann auch Snowboard fahren.“

(7 BE)

Die Zufallsgröße $Y$ gibt die von einem Besucher an einem Tag zurückgelegten Kilometer auf der Piste an und ist normalverteilt mit $\mu=22,5$ und $\sigma=5,5.$

Bestimme die Wahrscheinlichkeit dafür, dass die von einem Skifahrer an einem Tag auf der Piste zurückgelegten Kilometer um nicht mehr als eine halbe Standardabweichung vom Erwartungswert abweichen.

(3 BE)

Für ein $a\gt0$ liegen bei $35 \,\%$ aller Skifahrer die pro Tag auf der Piste zurückgelegten Kilometer im Intervall $[22,5-a ; 22,5+a].$

Ermittle den Wert von $a$ auf eine Nachkommastelle genau.

(3 BE)

Die Abbildung zeigt einen vereinfachten Ausschnitt des Pistenplans im Wintersportgebiet.

Besucher, die am Gipfel stehen, fahren mit einer Wahrscheinlichkeit von $0,6$ Piste 1. Danach nehmen sie entweder den Lift I zurück auf den Gipfel oder fahren Piste 2. Mit einer Wahrscheinlichkeit von $0,3$ nehmen die Besucher Lift I zurück auf den Gipfel.

Nach der Fahrt auf Piste 2 nehmen Besucher mit einer Wahrscheinlichkeit $p$ mit $0\lt p\lt1$ den Lift II. Alle anderen nehmen den Lift III.

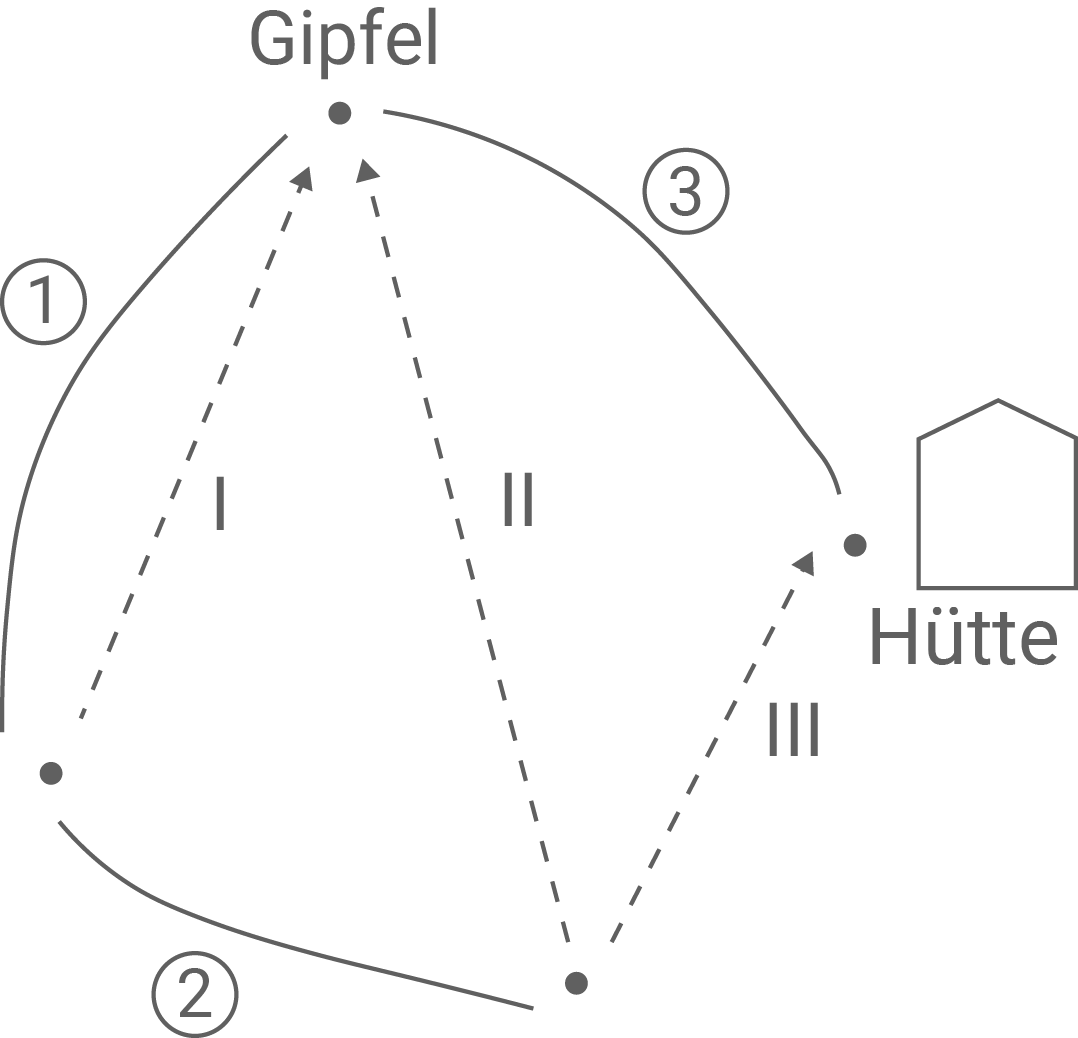
Schematische Darstellung eines Berggipfels mit verschiedenen Routen und einer Hütte.

Betrachtet werden Besucher, die vom Gipfel zur Hütte fahren und dabei noch genau eine Lifffahrt machen. Diese kommen mit einer höheren Wahrscheinlichkeit über die Piste 3 an als über den Lift III.

Berechne, welchen Wert $p$ mindestens hat.

(6 BE)

Aufgabe II 2

Für einen Ausbildungsplatz bei der Polizei müssen die Bewerber einen Eignungstest bestehen. Bei diesem müssen sie unter anderem ein Diktat schreiben. Erfahrungsgemäß bestehen $65$ Prozent der Bewerber das Diktat.

Untersucht wird zunächst eine Gruppe von $200$ Bewerbern.

Berechne jeweils die Wahrscheinlichkeit der folgenden Ereignisse:

$A:$

„In dieser Gruppe bestehen genau $125$ Bewerber das Diktat.“

$B:$

„In dieser Gruppe bestehen mindestens $60 \,\%$ der Bewerber das Diktat.“

(5 BE)

Bestimme die Wahrscheinlichkeit, dass die Anzahl der Bewerber, die das Diktat bestehen, um höchstens eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht.

(5 BE)

Erläutere in Bezug auf die Anwendungssituation, zu welchem Ereignis die Wahrscheinlichkeit mit folgendem Term berechnet wird:

$1-\displaystyle\sum_{i=0}^{30}\binom{200}{i} \cdot 0,35^i \cdot 0,65^{200-i}$

(2 BE)

Die Bewerber müssen die Mittlere Reife oder das Abitur als höchsten Schulabschluss vorweisen. Von den Bewerbern mit Abitur bestehen erfahrungsgemäß $80$ Prozent das Diktat, von den Bewerbern mit Mittlerer Reife bestehen erfahrungsgemäß nur $55$ Prozent das Diktat.

Ermittle die Wahrscheinlichkeit, dass ein zufällig ausgewählter Bewerber das Abitur als höchsten Schulabschluss hat.

(4 BE)

Betrachtet wird nun eine Gruppe von zufällig ausgewählten fünf Bewerbern. Bei diesen fünf Bewerbern wird ein Drogentest durchgeführt. Es wird davon ausgegangen, dass die Anzahl der bei dem Drogentest positiven Testergebnisse binomialverteilt ist. Die Wahrscheinlichkeit, dass mindestens einer der fünf Bewerber ein positives Testergebnis hat, beträgt gerundet $14,1 \,\%.$

Aus den fünf Bewerbern wird einer zufällig ausgewählt.
Berechne die Wahrscheinlichkeit, dass dieser ein positives Testergebnis hat.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung I 2

$8500\cdot0,2=1700$

$S$ beschreibt das Ereignis, dass ein Besucher Snowboard fahren kann. Mit den Wahrscheinlichkeiten aus den Aufgabenstellungen folgt:

$\begin{array}[t]{rlll} P(S\cap A)&=&P_S(A)\cdot P(S) \\[5pt] &=&0,4\cdot 0,2 \\[5pt] &=&0,08 \end{array}$

Damit ergibt sich folgende Vierfeldertafel:

	$\color{#fff}{A}$	$\color{#fff}{\overline{A}}$
$\color{#fff}{S}$	$0,08$	$0,12$	$0,2$
$\color{#fff}{\overline{S}}$	$0,75$	$0,05$	$0,8$
	$0,83$	$0,17$	$1$

Aus der Vierfeldertafel ergibt sich nun direkt $P(A)=0,83$ und $P(B)=0,75.$ Für die Wahrscheinlichkeit von Ereignis $C$ folgt:

$\begin{array}[t]{rlll} P(C)&=&P_A(S) \\[5pt] &=&\dfrac{P(A\cap S)}{P(A)} \\[5pt] &=&\dfrac{0,08}{0,83} \\[5pt] &\approx&0,096 \end{array}$

Es gilt $\mu+\frac{\sigma}{2}=25,25$ und $\mu-\frac{\sigma}{2}=19,75.$ Damit ergibt sich für die gesuchte Wahrscheinlichkeit:

$\begin{array}[t]{rlll} P(19,75\leq Y\leq 25,25)&\approx&0,383 \\[5pt] &=&38,3\,\% \end{array}$

Es ist der Wert von $a$ gesucht, sodass gilt:

$P(22,5-a \leq Y \leq 22,5+a)=0,35$

Aufgrund der Symmetrie der Wahrscheinlichkeitsverteilung ist das gleichbedeutend mit $P(22,5 \leq Y \leq 22,5+a)$ $=0,175.$
Systematisches Ausprobieren mit dem Taschenrechner liefert:

$a\approx2,5$

$A:$

„Ein Besucher kommt über die Piste 3 an.“

$B:$

„Ein Besucher kommt mit Lift III an.“

Für Ereignis $A$ gibt es zwei Möglichkeiten: Entweder, der Besucher fährt Piste 1 und nimmt dann Lift 1 bevor er Piste 3 nimmt, oder der Besucher fährt Pisten 1 und 2 und fährt dann mit Lift 2 zum Start von Piste 3. Damit ergibt sich:

$\begin{array}[t]{rlll} P(A)&=&0,6\cdot0,7\cdot p\cdot0,4+0,6\cdot0,3\cdot0,4 \\[5pt] &=&0,168p+0,072 \end{array}$

Bei Ereignis $B$ fährt der Besucher Pisten 1 und 2 und fährt dann mit Lift 3 zur Hütte. In diesem Fall folgt somit:

$\begin{array}[t]{rlll} P(B)&=&0,6\cdot0,7\cdot (1-p) \\[5pt] &=&0,42-0,42p \end{array}$

Für den minimalen Wert von $p$ folgt somit:

Rechenweg anzeigen

$p \gt 0,592$

Lösung II 2

Die Zufallsvariable $X,$ die die Anzahl der Bewerber angibt, die das Diktat bestehen, ist binomialverteilt mit $n=200$ und $p=0,65.$ Damit ergibt sich:

$\begin{array}[t]{rlll} P(A)&=&P(X=125) \\[5pt] &\approx&0,044 \\[5pt] &=&4,4\,\% \end{array}$

$\begin{array}[t]{rlll} P(B)&=&P(X\geq0,6\cdot200) \\[5pt] &=&P(X\geq120) \\[5pt] &=&1-P(X\leq119) \\[5pt] &\approx&0,939 \\[5pt] &=&93,9\,\% \end{array}$

Für den Erwartungswert und die Standardabweichung von $X$ ergibt sich:

$\mu=n\cdot p=200\cdot0,65=130$

$\begin{array}[t]{rlll} \sigma&=&\sqrt{n\cdot p\cdot (1-p)} \\[5pt] &=&\sqrt{200\cdot 0,65\cdot 0,35} \\[5pt] &\approx&6,75 \end{array}$

Damit folgt für die gesuchte Wahrscheinlichkeit:

Rechenweg anzeigen

$P\left(\mu-\dfrac{\sigma}{2}\leq X\leq\mu+\dfrac{\sigma}{2}\right) = 39,6\,\%$

Mindestens $31$ Bewerber bestehen das Diktat nicht

$A:$

„Ein Bewerber hat das Abitur als höchsten Schulabschluss.“

$D:$

„Ein Bewerber hat das Diktat bestanden.“

Für die gesuchte Wahrscheinlichkeit ergibt sich:

Rechenweg anzeigen

$P(A)=0,4$

Die Zufallsvariable $Y,$ die die Anzahl der Bewerber angibt, die ein positives Testergebnis haben, ist binomialverteilt mit $n=5$ und unbekanntem $p.$ Mit der Gegenwahrscheinlichkeit des Ereignisses aus der Aufgabenstellung ergibt sich für $p:$

$\begin{array}[t]{rlll} P(Y=0)&\approx&1-0,141 \\[5pt] (1-p)^5&\approx&0,859 &\mid\;\sqrt[5]{\;} \\[5pt] 1-p&\approx&\sqrt[5]{0,859} &\mid\;-1 \\[5pt] -p&\approx&\sqrt[5]{0,859}-1 &\mid\;\cdot(-1) \\[5pt] p&\approx&0,03 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?