Lineare Algebra

Aufgabe I 3

Gegeben sind die Punkte $A(-3\mid-2\mid 5), B(1\mid-2\mid 3), C(9\mid6\mid 7)$ und $D(5\mid6\mid 9).$

Zeige, dass das Viereck $ABCD$ ein Parallelogramm ist.

(2 BE)

Zeichne das Parallelogramm $ABCD$ in ein dreidimensionales Koordinatensystem.

(3 BE)

Weise nach, dass die $x_3$ -Achse das Parallelogramm $A B C D$ schneidet.

(5 BE)

Die Gerade $g$ verläuft parallel zur $x_3$ -Achse durch Punkt $C.$
Die Gerade $h$ verläuft senkrecht zum Parallelogramm durch Punkt $C.$
Berechne den Winkel, unter dem sich die beiden Geraden schneiden.

(4 BE)

Eine Ebene $F$ ist parallel zur $x_1 x_3$ -Ebene und teilt das Parallelogramm in zwei Teilflächen.

Begründe, dass es sich bei beiden Teilflächen wieder um Parallelogramme handelt.
Das Verhältnis der Flächeninhalte dieser beiden Teilflächen beträgt $1: 2.$
Ermitttle die Koordinaten des Schnittpunktes der Ebene $F$ mit der Seite $BC.$ Begründe dein Vorgehen.

(6 BE)

Aufgabe II 3

Ein Kirchturm hat einen quadratischen Grundriss. In einer gewissen Höhe geht der Kirchturm in ein achteckiges Prisma über. Das Dach hat die Form einer achteckigen Pyramide.

Der obere Teil des Kirchturms ist in der Abbildung dargestellt. Der quadratische Grundriss des Turms hat eine Seitenlänge von $6$ Metern.

Die Punkte $A_1(3\mid3\mid 0), A_2(-3\mid3\mid 0),$ ... liegen in der $x_1 x_2$ -Ebene. Folgende weitere Punkte sind gegeben:

$B_1(3\mid3\mid 2), B_2(-3\mid3\mid 2)$
$C_1(3\mid1\mid 4), C_2(1\mid3\mid 4), C_3(-1\mid3\mid 4)$
$D_1(3\mid1\mid 8), D_2(1\mid3\mid 8), D_3(-1\mid3\mid 8)$

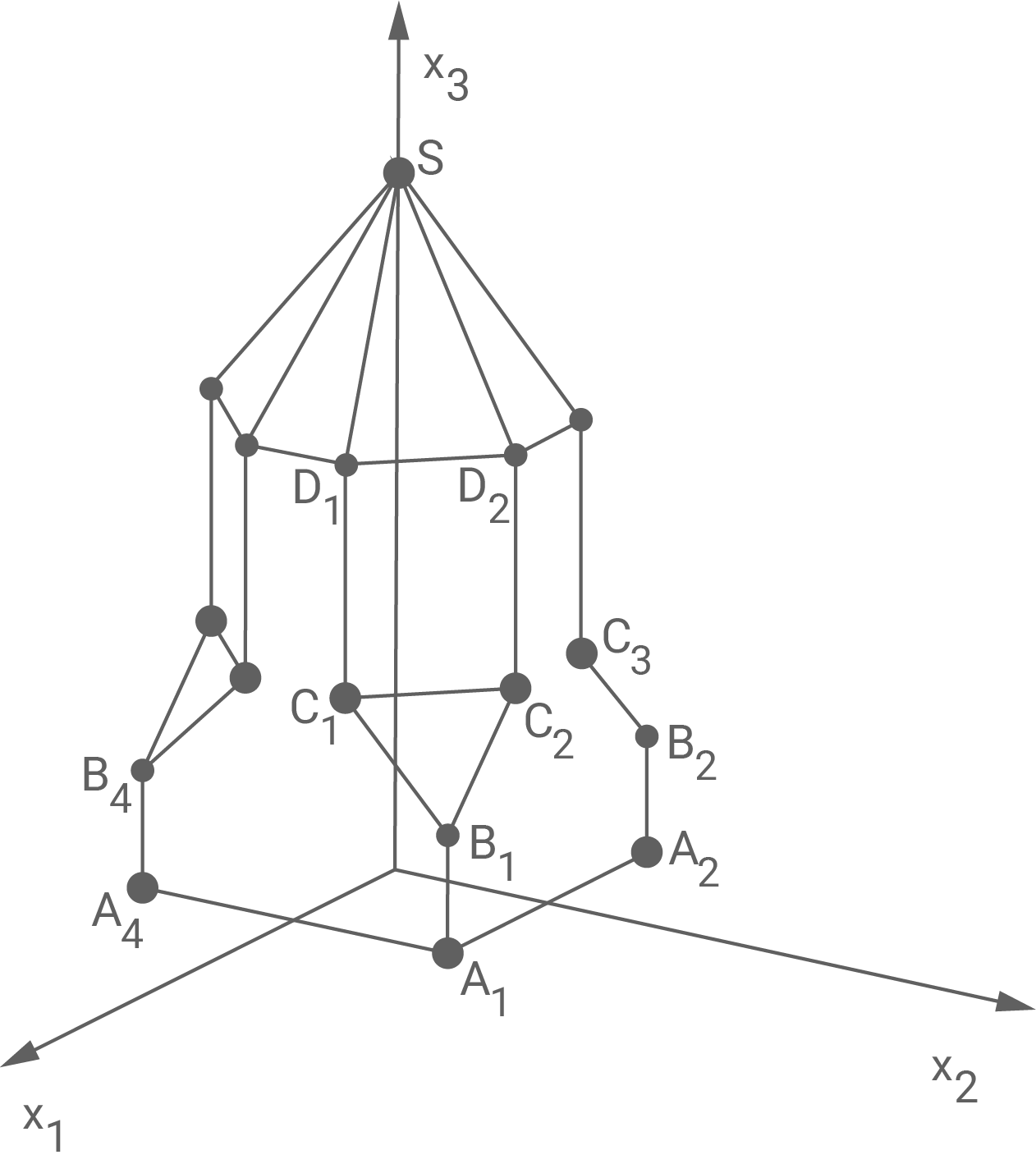
Dreidimensionales Diagramm mit Punkten und Linien in einem Koordinatensystem.

Alle Punkte $B_{...}$ haben die $x_3$ -Koordinate $2.$ Alle Punkte $C_{...}$ haben die $x_3$ -Koordinate $4.$
Alle Punkte $D_{...}$ haben die $x_3$ -Koordinate $8.$ Eine Längeneinheit entspricht $1$ Meter.

Zeichne das Quadrat $A_1 A_2 A_3 A_4$ in ein zweidimensionales $x_1 x_2$ -Koordinatensystem ein.
Zeichne in dasselbe Koordinatensystem die orthogonalen Projektionen der Punkte $C_1$ und $C_2$ ein.

(5 BE)

Zeige, dass das Dreieck $C_1 B_1 C_2$ gleichseitig ist.
Berechne den Flächeninhalt des Dreiecks $C_1 B_1 C_2.$

(5 BE)

Die Spitze $S$ liegt auf der $x_3$ -Achse.

Vier der acht Dreiecksflächen des Daches sind parallel zu den jeweils unterhalb liegenden Dreiecksflächen.
Ermittle die Koordinaten der Spitze $S.$

(3 BE)

Der Mittelpunkt der Strecke $D_1 D_2$ ist $M.$ Der Mittelpunkt der Strecke $D_2 D_3$ ist $N.$
Begründe, dass die Strecken $MS$ und $NS$ unterschiedliche Neigungswinkel haben.

(3 BE)

Der Kirchplatz liegt in einer zur $x_1 x_2$ -Ebene parallelen Ebene. Die Spitze $S$ befindet sich $30\; \text{m}$ über dem Kirchplatz.

An einem Sommertag scheint die Sonne in der Richtung $\overrightarrow{v}=\pmatrix{3\\2\\-4}.$ Dadurch wirft sie einen Schatten von $S$ auf den Kirchplatz.
Berechne, wie groß der Abstand der Spitze $S$ von deren Schattenpunkt ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung I 3

$\begin{array}[t]{rlll} \overrightarrow{AB}&=& \pmatrix{1-(-3)\\-2-(-2)\\3-5}\\[5pt] &=&\pmatrix{4\\0\\-2} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{DC}&=& \pmatrix{9-5\\6-6\\7-9}\\[5pt] &=&\pmatrix{4\\0\\-2} \end{array}$

Da die beiden gegenüberliegenden Kanten $\overline{AB}$ und $\overline{CD}$ somit parallel und gleichlang sind, ist das Viereck $ABCD$ ein Parallelogramm.

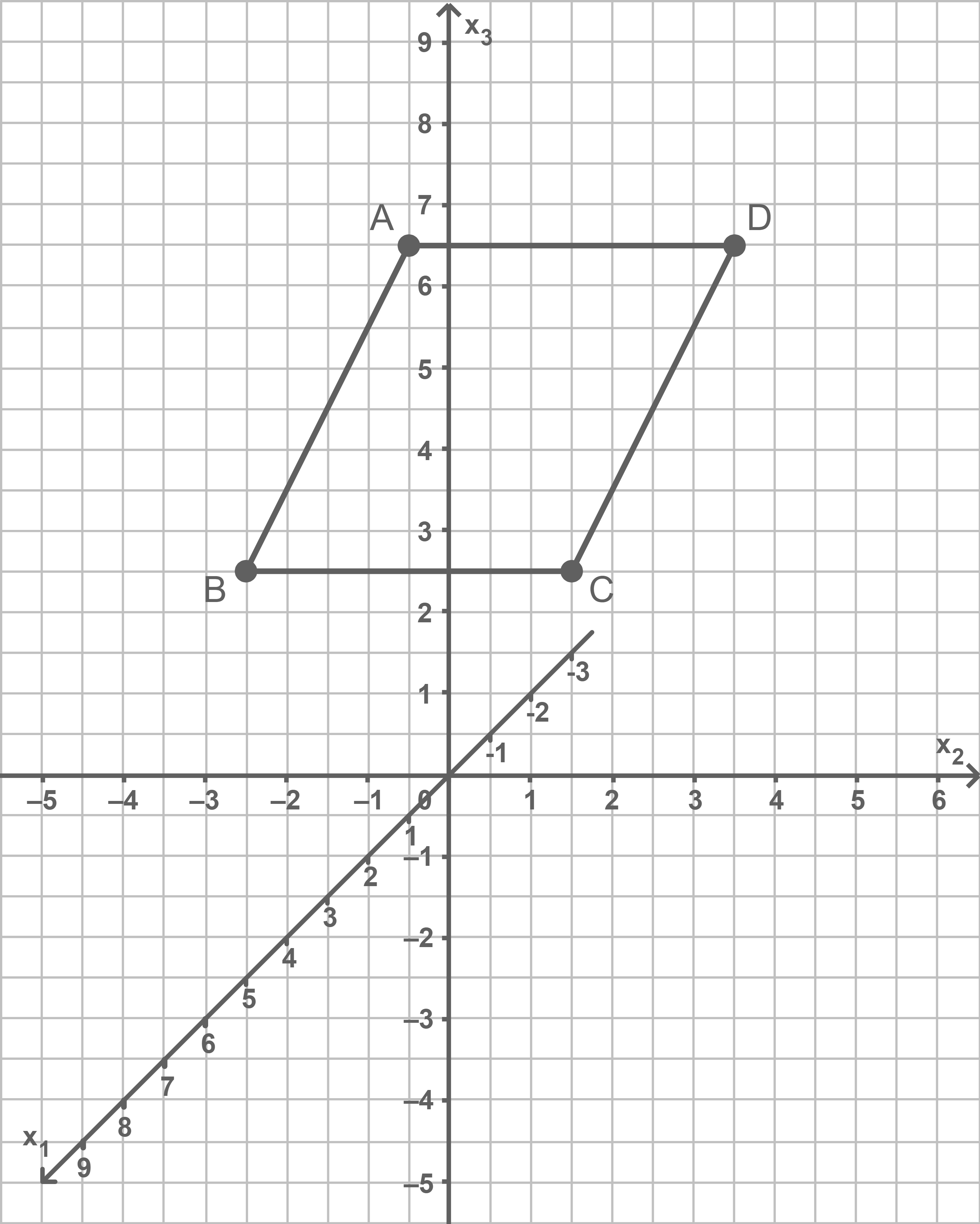
Diagramm mit Koordinatenpunkten A, B, C, D und einer Linie in einem Gitter.

$\begin{array}[t]{rlll} \overrightarrow{AD}&=& \pmatrix{5-(-3)\\6-(-2)\\9-5}\\[5pt] &=&\pmatrix{8\\8\\4} \end{array}$

Mit $\overrightarrow{OA}$ als Stützvektor und $\overrightarrow{AB}$ sowie $\overrightarrow{AD}$ als Spannvektoren, folgt für die Ebenengleichung der Ebene, in der das Parallelogramm $ABCD$ liegt:

$E:\overrightarrow{x}=\pmatrix{-3\\-2\\5}+s\cdot\pmatrix{4\\0\\-2}+t\cdot\pmatrix{8\\8\\4}$

Nullsetzen der ersten beiden Koordinaten liefert folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&-3+4s+8t&=&0 \\ \text{II}\quad&-2+8t&=&0 \\ \end{array}$

Gleichung $\text{II}$ liefert direkt $t=\frac{1}{4}.$ Einsetzen in Gleichung $\text{I}$ ergibt für $s:$

$\begin{array}[t]{rlll} -3+4s+8\cdot\dfrac{1}{4}&=&0 &\mid\;+1 \\[5pt] 4s&=&1 &\mid\;:4 \\[5pt] s&=&\dfrac{1}{4} \end{array}$

Da die Spannvektoren der Ebene genau die Vektoren der Seiten $\overline{AB}$ und $\overline{AD}$ sind, folgt aus $0\lt s\lt 1$ und $0\lt t\lt 1,$ dass der Schnittpunkt der Ebene mit der $x_3$ -Achse innerhalb des Parallelogramms liegt, dieses also von der $x_3$ -Achse geschnitten wird.

Für einen Normalenvektor der Ebene $E$ folgt mit dem Kreuzprodukt:

$\begin{array}[t]{rlll} \overrightarrow{n}&=&\pmatrix{4\\0\\-2}\times\pmatrix{8\\8\\4} \\[5pt] &=&\pmatrix{0-(-2\cdot8)\\(-2)\cdot8-4\cdot4\\4\cdot8-0} \\[5pt] &=&\pmatrix{16\\-32\\32} \end{array}$

Mit dem gekürzten Vektor $\frac{1}{16}\cdot\overrightarrow{n}$ folgt dann für den gesuchten Winkel:

$\begin{array}[t]{rlll} \cos(\alpha)&=&\dfrac{\left\vert\pmatrix{1\\-2\\2}\circ\pmatrix{0\\0\\1}\right\vert}{\left\vert\pmatrix{1\\-2\\2}\right\vert\cdot\left\vert\pmatrix{0\\0\\1}\right\vert} \\[5pt] \cos(\alpha)&=&\dfrac{2}{\sqrt{1^2+(-2)^2+2^2}\cdot\sqrt{1^2}} \\[5pt] \cos(\alpha)&=&\dfrac{2}{3} \\[5pt] \alpha&=&\cos^{-1}\left(\dfrac{2}{3}\right) \\[5pt] \alpha&\approx&48,2^\circ \end{array}$

Parallelogramme begründen

Die Vektoren $\overrightarrow{AB}$ bzw. $\overrightarrow{CD}$ haben die $x_2$ -Koordinate $0,$ d.h. die zugehörigen Seiten $\overline{AB}$ und $\overline{CD}$ liegen parallel zur $x_1 x_3$ -Ebene. Damit sind die beiden Teilflächen wieder Parallelogramme.

Koordinaten ermitteln

Da die Grundseiten der beiden Teilparallelogramme gleich lang sind, ist das Verhältnis der Flächeninhalte das gleiche wie das Verhältnis der beiden Höhen. Somit ist das auch das Verhältnis, in dem $F$ die Seite $\overline{BC}$ teilt. Für den Ortsvektor des gesuchten Schnittpunkts folgt somit z.B.:

$\begin{array}[t]{rlll} \overrightarrow{OP}&=&\overrightarrow{OB}+\dfrac{1}{3}\cdot\overrightarrow{B C} \\[5pt] &=&\pmatrix{1\\-2\\3}+\dfrac{1}{3}\cdot\pmatrix{8\\8\\4} \\[5pt] &=&\pmatrix{\frac{11}{3}\\\frac{2}{3}\\\frac{13}{3}} \end{array}$

Die Koordinaten eines möglichen Schnittpunktes sind somit durch $P(\frac{11}{3}\mid\frac{2}{3}\mid\frac{13}{3})$ gegeben.

Lösung II 3

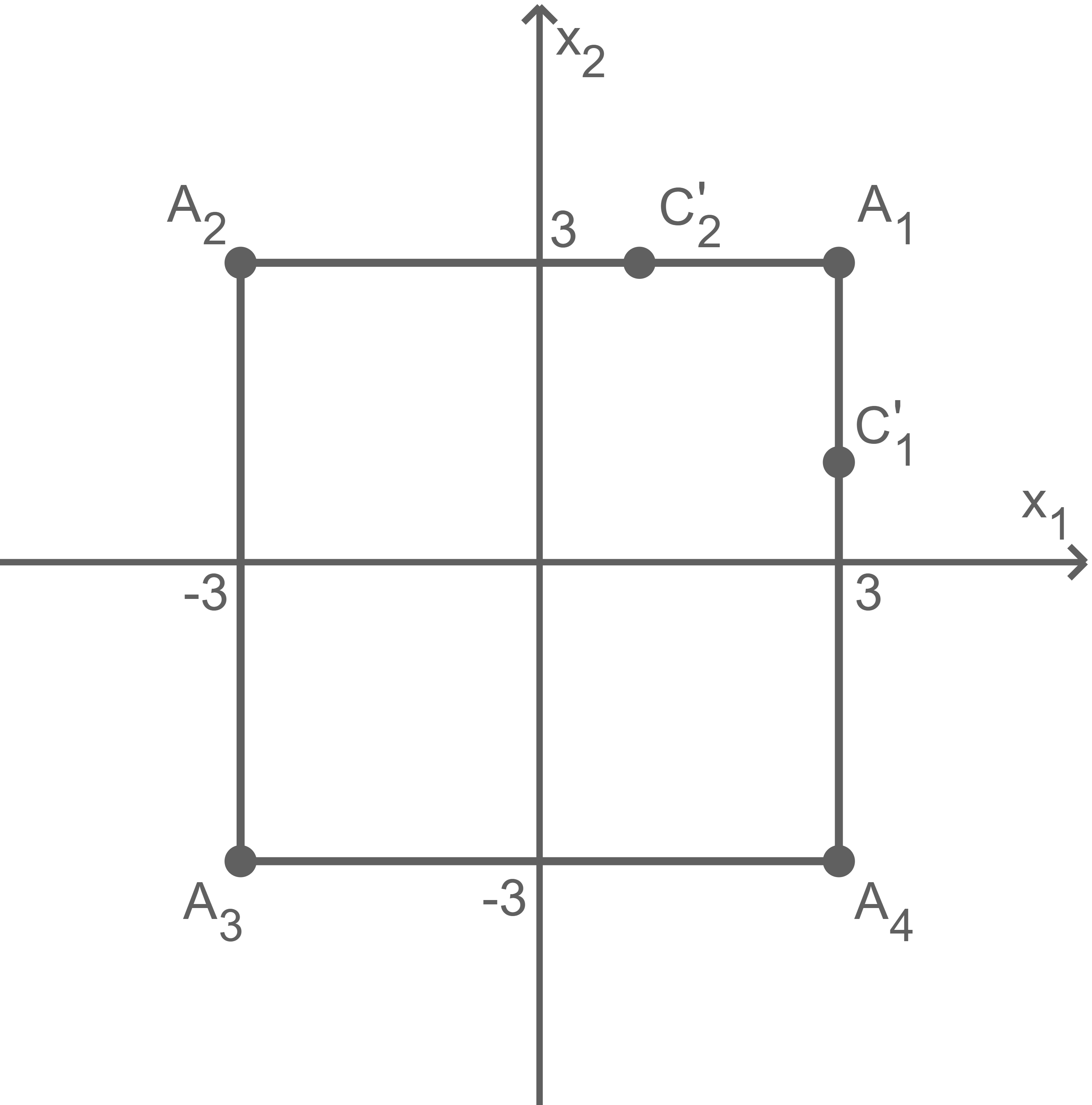
Grafik eines Koordinatensystems mit Punkten A1, A2, A3, A4 und C1, C2.

Gleichseitigkeit zeigen

$\begin{array}[t]{rlll} \left\vert\overrightarrow{B_1C_1}\right\vert&=&\left\vert\pmatrix{3-3\\1-3\\4-2}\right\vert \\[5pt] &=&\sqrt{(-2)^2+2^2} \\[5pt] &=&\sqrt{8} \end{array}$

$\begin{array}[t]{rlll} \left\vert\overrightarrow{B_1C_2}\right\vert&=&\left\vert\pmatrix{1-3\\3-3\\4-2}\right\vert \\[5pt] &=&\sqrt{(-2)^2+2^2} \\[5pt] &=&\sqrt{8} \end{array}$

$\begin{array}[t]{rlll} \left\vert\overrightarrow{C_1C_2}\right\vert&=&\left\vert\pmatrix{1-3\\3-1\\4-4}\right\vert \\[5pt] &=&\sqrt{(-2)^2+2^2} \\[5pt] &=&\sqrt{8} \end{array}$

Da $\left\vert\overrightarrow{B_1C_1}\right\vert=\left\vert\overrightarrow{B_1C_2}\right\vert=\left\vert\overrightarrow{C_1C_2}\right\vert$ gilt, ist das Dreieck gleichseitig.

Flächeninhalt berechnen

Anhand der Koordinaten von $C_1$ und $C_2$ lässt sich erkennen, dass der Mittelpunkt der Strecke die Koordinaten $M(2\mid2\mid4)$ besitzt. Damit folgt für den Flächeninhalt $A$ des Dreiecks:

$\begin{array}[t]{rlll} A&=&\dfrac{1}{2}\cdot\left\vert\overrightarrow{C_1C_2}\right\vert\cdot\left\vert\overrightarrow{MB_1}\right\vert \\[5pt] &=&\dfrac{1}{2}\cdot\sqrt{8}\cdot\left\vert\pmatrix{3-2\\3-2\\2-4}\right\vert \\[5pt] &=&\dfrac{1}{2}\cdot\sqrt{8}\cdot\sqrt{6} \\[5pt] &=& 2\sqrt{3} \end{array}$

Für einen Normalenvektor der Ebene, in der das Dreieck $C_1B_1C_2$ liegt, folgt:

$\begin{array}[t]{rlll} \overrightarrow{n}&=&\overrightarrow{B_1C_1}\times\overrightarrow{B_1C_2} \\[5pt] &=&\pmatrix{0\\-2\\2}\times\pmatrix{-2\\0\\2} \\[5pt] &=&\pmatrix{-2\cdot2\\2\cdot(-2)\\-((-2)\cdot(-2))} \\[5pt] &=&\pmatrix{-4\\-4\\-4} \end{array}$

Da die Ebene, in der die Punkte $D_1, D_2$ und $S$ liegen, parallel zu der Ebene des Dreiecks $C_1B_1C_2$ ist, folgt mit dem Normalenvektor $-\frac{1}{4}\cdot\overrightarrow{n}$ folgende allgemeine Ebenengleichung:

$F:x_1+x_2+x_3=d$

Einsetzen der Koordinaten von z.B. $D_1$ liefert:

$\begin{array}[t]{rlll} 3+1+8&=&d \\[5pt] 12&=&d \end{array}$

Da $S$ auf der $x_3$ -Achse liegt, gilt somit $S(0\mid0\mid12).$

Aus den Koordinaten der Punkte $D_{\ldots}$ folgt $M(2\mid2\mid8)$ und $N(0\mid3\mid8).$ Der Abstand von $M$ zur $x_3$ -Achse beträgt somit $\sqrt{2^2+2^2}=\sqrt{8}$ und der Abstand von $N$ zur $x_3$ -Achse beträgt $\sqrt{3^2}=3.$
Da $M$ damit näher an der $x_3$ -Achse liegt, ist die Verbindung zu $S$ steiler als bei $N,$ d.h. die Neigungen der Strecken $MS$ und $NS$ sind unterschiedlich.

Für die Gleichung der Geraden, entlang der die Sonnenstrahlen verlaufen, folgt:

$g:\overrightarrow{x}=\pmatrix{0\\0\\12}+s\cdot\pmatrix{3\\2\\-4}$

Nullsetzen der dritten Koordinate liefert für $s:$

$\begin{array}[t]{rlll} 12-4s&=&0 &\mid\;-12 \\[5pt] -4s&=&-12 &\mid\;:(-4) \\[5pt] s&=&3 \end{array}$

Damit ergeben sich die Koordinaten des Schattenpunkts von $S$ als $\(S$ Für den Abstand dieses Punktes von $S$ folgt:

$\(\begin{array}[t]{rlll} \left\vert\overrightarrow{SS$

Aus der Aufgabenstellung folgt, dass $12\;\text{LE}\mathrel{\widehat{=}}30\;\text{m}$ gilt. Damit folgt, dass die Spitze des Kirchturms $\sqrt{261}\cdot\frac{30}{12}\approx40,4\;[\text{m}]$ von ihrem Schattenpunkt entfernt ist.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?