Analysis
Aufgabe I 1
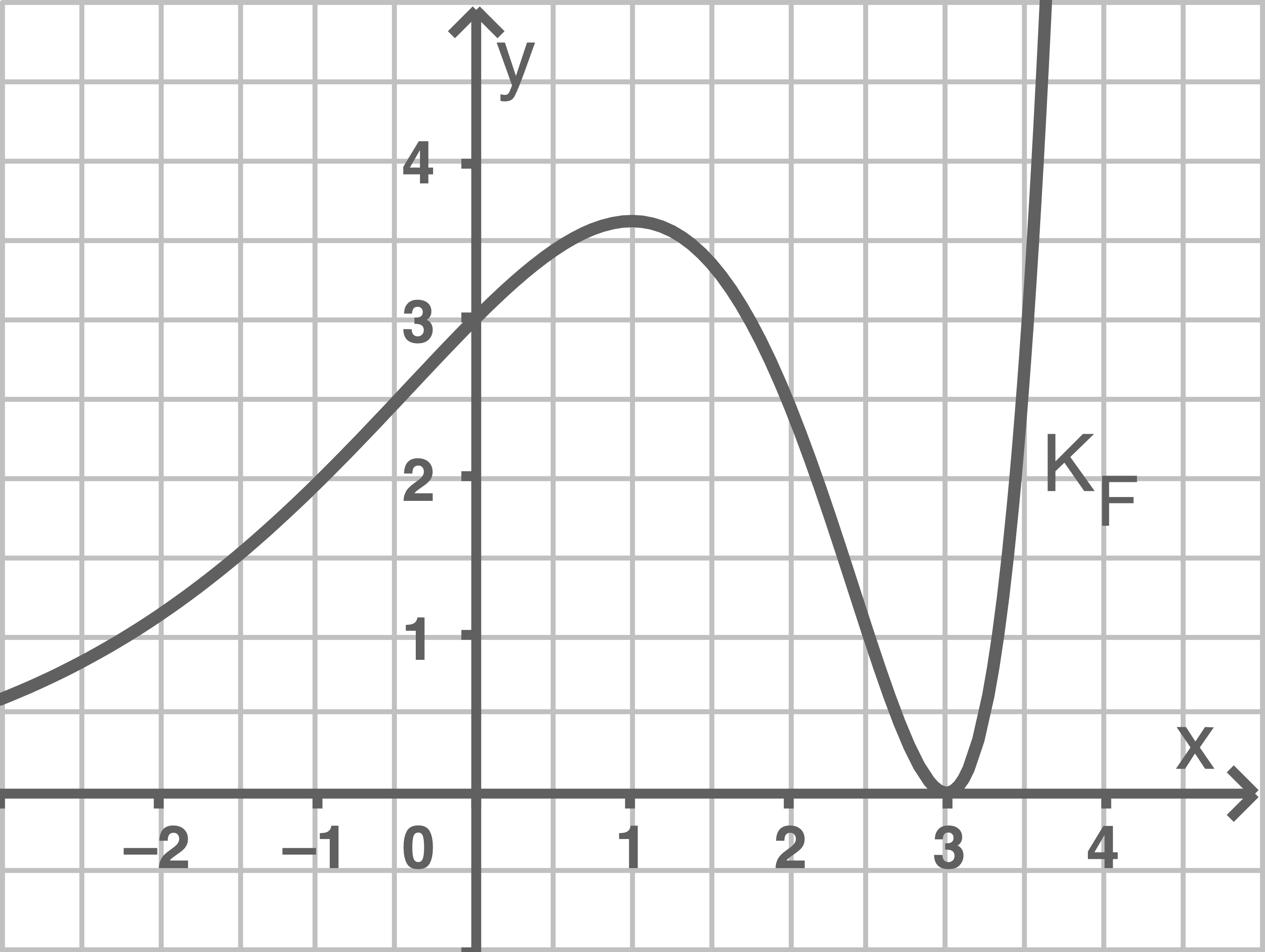
Der Graph einer in
definierten quadratischen Funktion
schneidet die
-Achse im Punkt
In diesem Punkt hat
die Steigung
Der Tiefpunkt von
hat die
-Koordinate
Bestimme eine Gleichung der Funktion
Zur Kontrolle:
Zeichne im Bereich
Berechne den Inhalt der Fläche, die mit der
-Achse einschließt.
Die Funktion ist für
definiert durch
Der Graph von ist
Die Funktion ist für
definiert durch
Zeige, dass eine Stammfunktion von
ist.
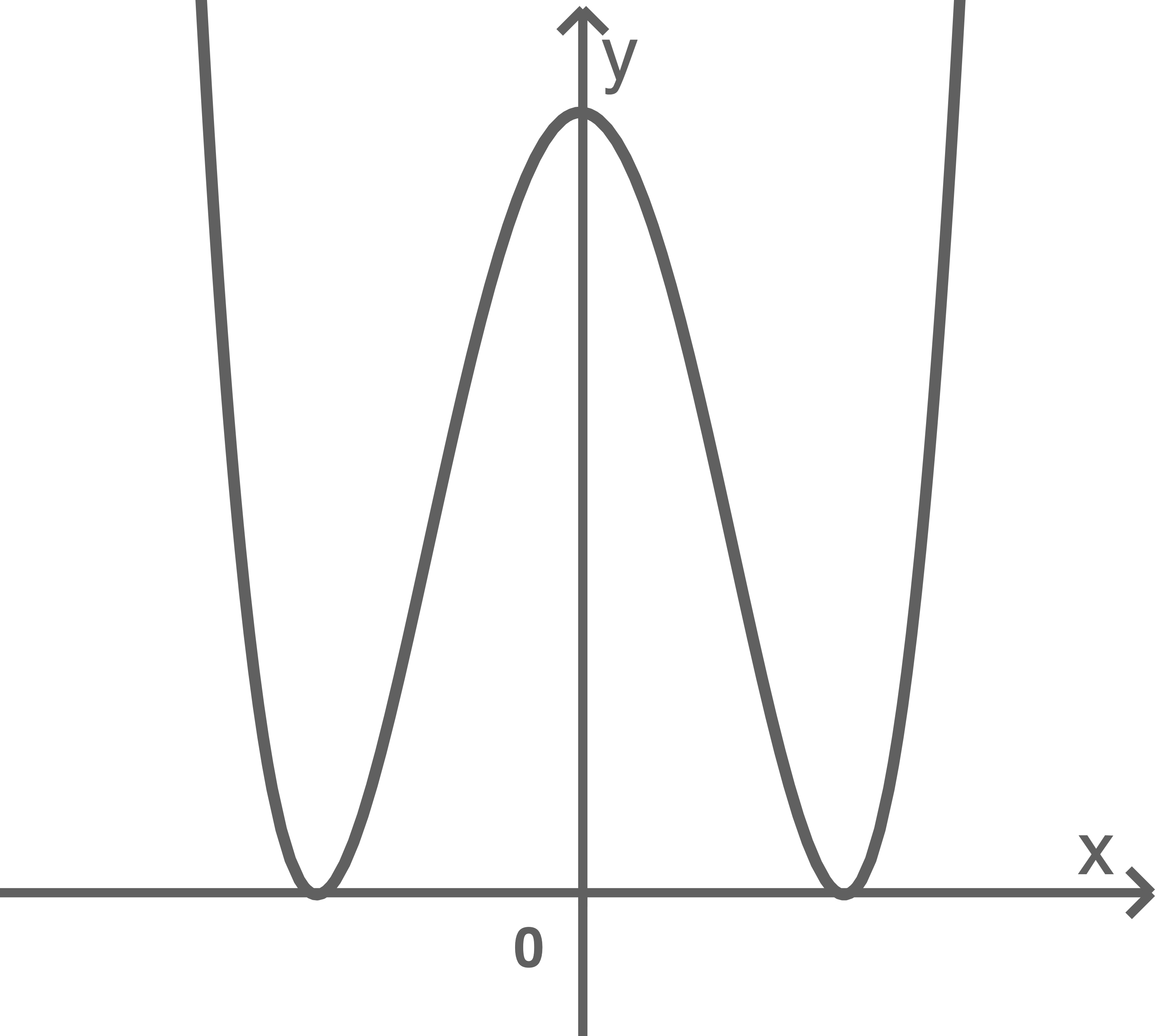
Die Abbildung zeigt einen Ausschnitt des Graphen der Funktion
Entscheide, ob die folgenden Aussagen wahr oder falsch sind.
Begründe deine Entscheidung jeweils mithilfe von
besitzt genau einen Extrempunkt im Intervall
- Es gilt:
- Es gilt:
Der Graph der Funktion entsteht, indem
zuerst um
nach rechts verschoben und dann an der
-Achse gespiegelt wird.
Begründe, dass die folgenden Aussagen korrekt sind:
- Die Reihenfolge der beiden Transformationen spielt eine Rolle.
- Die Funktion
mit
ist eine Stammfunktion von
Die folgende Abbildung zeigt den Graphen einer Stammfunktion
von
für
Die positive -Achse ist Asymptote von
Zudem ist
in diesem Bereich streng monoton steigend.
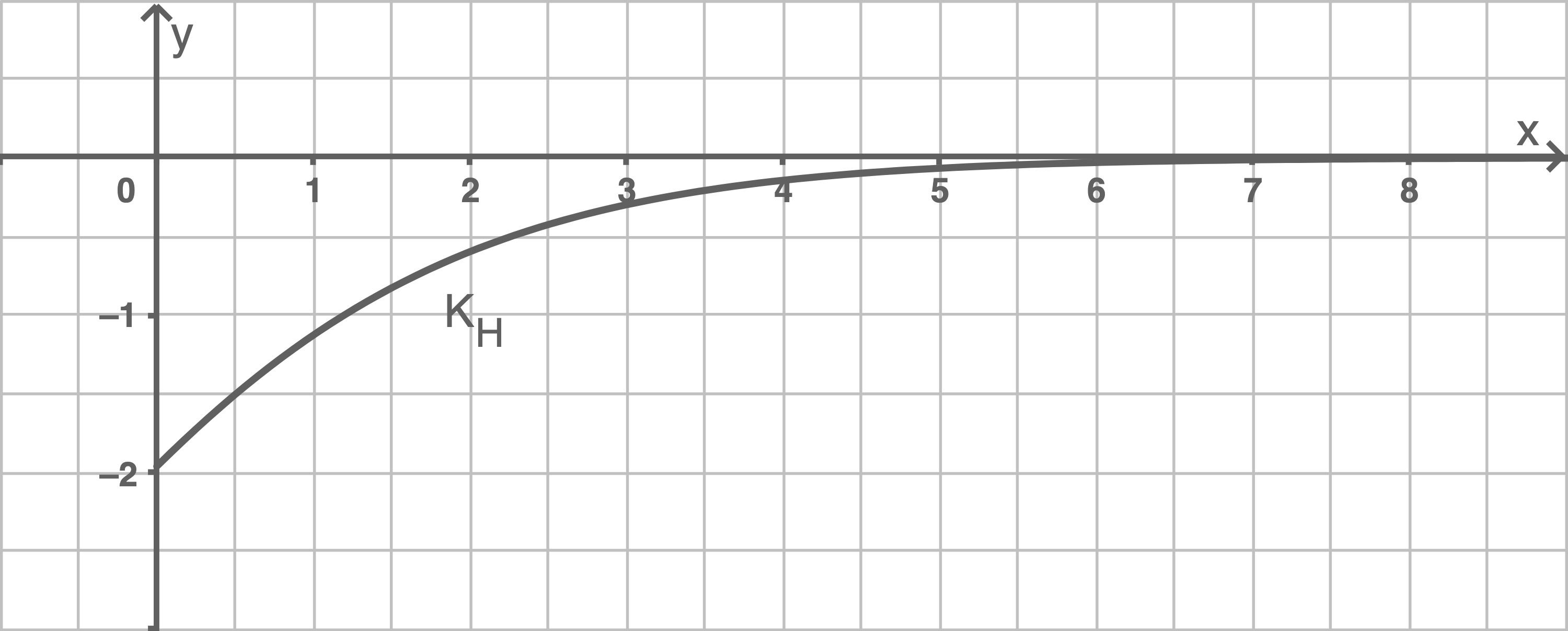
Die Integralfunktion ist definiert durch
Begründe mit Hilfe von dass
Aufgabe II 1
Gegeben ist die in definierte Funktion
durch
Der Graph von ist
Nenne drei Argumente, warum es sich beim dargestellten Graphen um handeln kann.
Der Graph der Funktion
mit
geht aus
durch Streckung in
-Richtung mit dem Faktor
hervor.
Gib den Wert von an.
Bestimme eine Gleichung der Parabel (zweiten Grades), die durch alle Extrempunkte von verläuft.
Die Gerade mit der Gleichung schließt mit dem Graphen
drei Teilflächen ein. Zeige, dass man diese Gerade nach unten verschieben muss, damit die eingeschlossenen Teilflächen alle denselben Flächeninhalt haben.
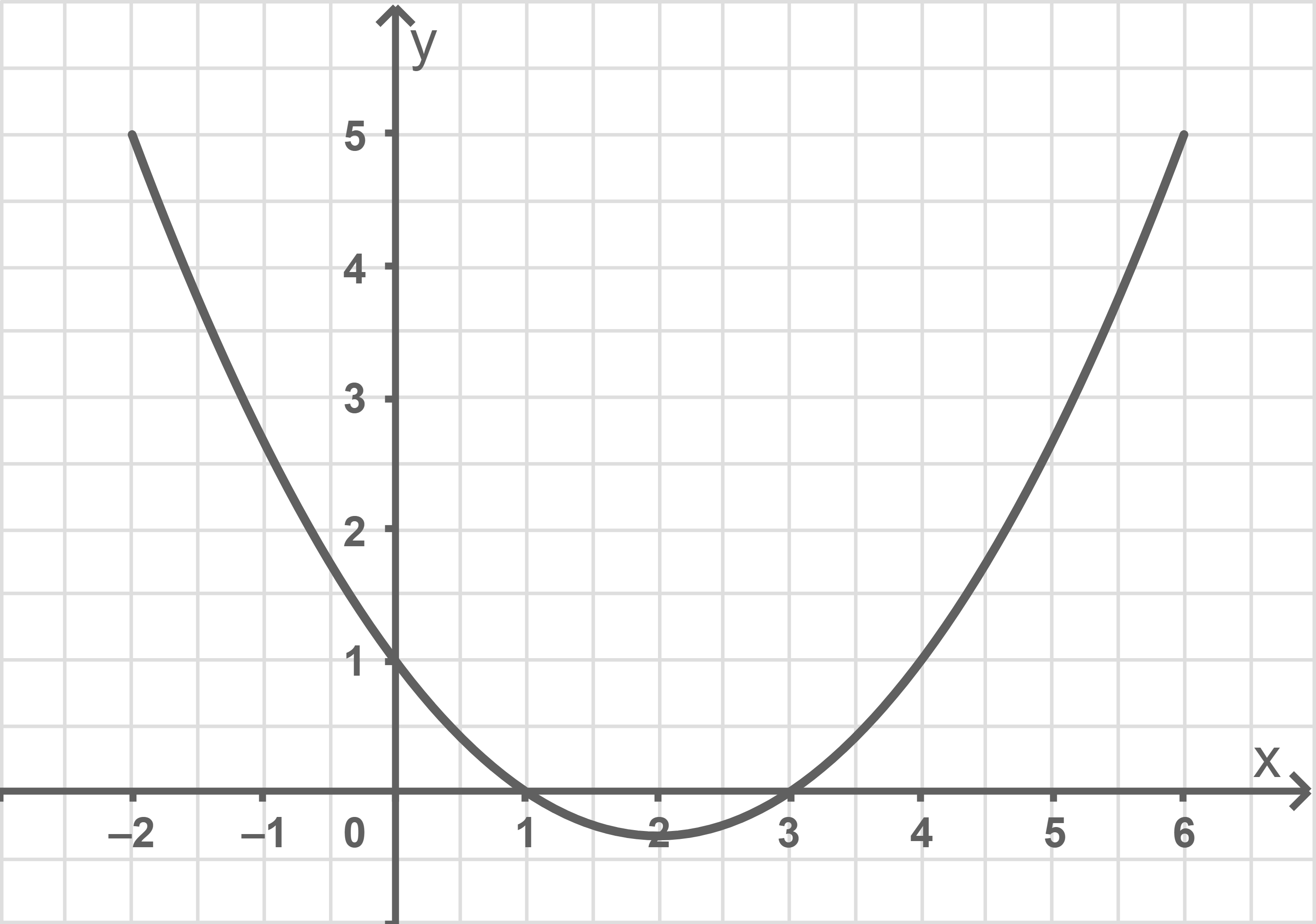
Gegeben ist die Funktion mit
Ihr Graph ist
Zeichne im Bereich
Zeige, dass die Gerade mit der Gleichung
eine Tangente an den Graphen
im Punkt
ist.
Die Tangente im Kurvenpunkt schneidet die
-Achse im Punkt
Bestimme denjenigen Wert, den die -Koordinate von
maximal annehmen kann.
Ein Notizzettel hat die Maße Von diesem Notizzettel wird nun immer wieder ein Stück abgeschnitten, so dass sich der Flächeninhalt
des verbleibenden Stücks mit jedem Schnitt halbiert.
Zeige, dass sich der nach Schnitten verbleibende Flächeninhalt des Notizzettels in
durch die Funktion
mit
beschreiben lässt.
Berechne, wie oft man ein Stück des Notizzettels abschneiden muss, bis das verbleibende Stück erstmals einen Flächeninhalt von weniger als einem hundertstel Quadratzentimeter hat.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung I 1
Die Funktion hat die allgemeine Funktionsgleichung
Für die Ableitung gilt somit
Einsetzen der Informationen aus der Aufgabenstellung liefert:
Für ergibt sich:
Für gilt somit:
Damit ergibt sich insgesamt
Mit Hilfe des Graphen aus Aufgabenteil b lässt sich ablesen, dass und
die Nullstellen von
sind und der Graph zwischen diesen unterhalb der
-Achse verläuft. Damit folgt für den gesuchten Flächeninhalt:
Mit der Produktregel folgt:
- Der Graph
besitzt im Intervall
zwei Wendepunkte. Damit besitzt
in diesem Intervall zwei Extrempunkte und die Aussage ist falsch.
- Anhand der Abbildung lässt sich erkennen, dass die Steigung der Tangente an
an der Stelle
ungefähr
beträgt, d. h. es gilt
Diese Aussage ist somit ebenfalls falsch.
- Diese Aussage ist wahr, da
an dieser Stelle rechtsgekümmt ist.
Aussage 1:
Der Graph von besitzt die Nullstellen
und
Wenn er zuerst verschoben und dann gespiegelt wird, besitzt die Funktion
die Nullstellen
und
Im Fall, dass zuerst gespiegelt und dann verschoben wird, hat stattdessen die Nullstellen
und
Damit entstehen also unterschiedliche Graphen und Aussage 1 ist korrekt.
Aussage 2:
Es gilt Ableiten von
mit der Kettenregel liefert:
Aussage 2 ist somit ebenfalls korrekt.
Es gilt:
Da die -Achse die Asymptote des Graphen von
ist, gilt
Damit ergibt sich
Lösung II 1
- Der Graph besitzt keine negativen Werte.
- Der Graph weist zwei doppelte Nullstellen auf.
- Die Nullstellen des Graphen liegen symmetrisch zur
-Achse.
Da aus
durch Streckung in
-Richtung entsteht, besitzt auch
die Nullstellen
und
die jeweils Tiefpunkte sind. Der Hochpunkt liegt auch bei
auf der
-Achse, somit folgt für dessen
-Koordinate:
Damit ergibt sich die allgemeine Gleichung der Parabel. Einsetzen der Koordinaten einer der beiden Tiefpunkte liefert:
Die Gleichung der Parabel ergibt sich somit als
Für die Schnittstellen der Gerade mit dem Graphen folgt:
Mit dem Satz des Nullprodukts folgen die Schnittpunkte
und
Für die Flächeninhalte der letzten beiden eingeschlossenen Flächen folgt damit:
Die erste und die letzte Fläche, d. h. die beiden Flächen unterhalb der Geraden, sind aufgrund der Symmetrie gleich groß. Da die Fläche oberhalb der Geraden somit kleiner ist, als die beiden unterhalb der Geraden, muss die Gerade nach unten verschoben werden.
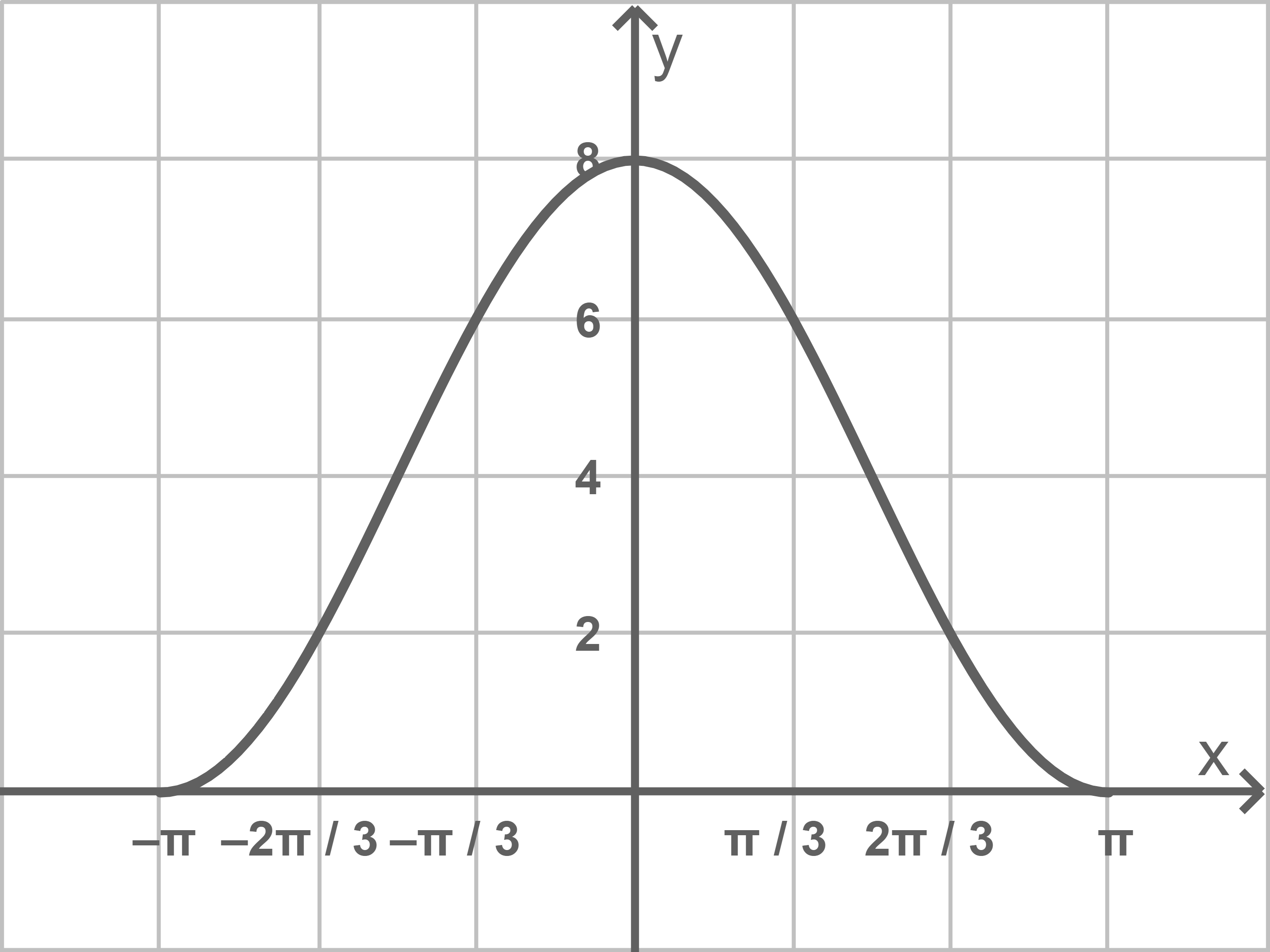
Für die erste Ableitung von ergibt sich:
Im Punkt hat
somit die folgende Steigung:
Durch Ablesen in der Gleichung von folgt, dass
auch die Steigung von
ist. Einsetzen der Koordinaten von
in die Gleichung von
liefert zudem:
Für gilt zudem:
Da somit ebenfalls durch
verläuft und in diesem Punkt zudem die gleiche Steigung wie
besitzt, ist
eine Tangente an den Graphen
im Punkt
Für die Steigung von in
gilt
Die allgemeine Tangentengleichung ergibt sich somit als
Einsetzen der Koordinaten von
liefert für
Ableiten des Wertes von nach
mit der Produktregel liefert:
Die notwendige Bedingung für Extremstellen liefert weiter:
Mit dem Satz des Nullprodukts ergibt sich und
da der Kosinus für
nur bei
Null wird. Überprüfen der Intervallgrenzen liefert:
Die -Koordinate von
entspricht
und nimmt somit maximal einen Wert von ca.
an.
Es gilt Da sich der Flächeninhalt mit jedem Schnitt halbiert, folgt:
Da ist, muss somit mindestens
-mal ein Stück des Notizzettels abgeschnitten werden, bis das verbleibende Stück erstmals einen Flächeninhalt von weniger als einem hundertstel Quadratzentimeter hat.