Vermischte Aufgaben Funktionsgleichungen aufstellen
1.
Gegeben sind die Schaubilder einiger ganzrationaler Funktionen. Bestimme einen möglichen Funktionsterm.
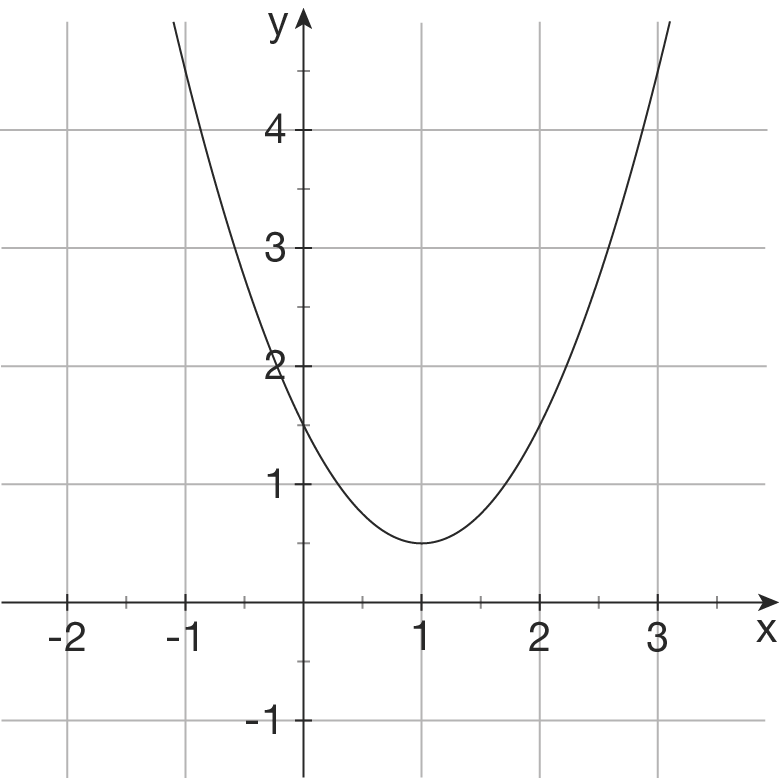
a)

b)
Hinweis: 
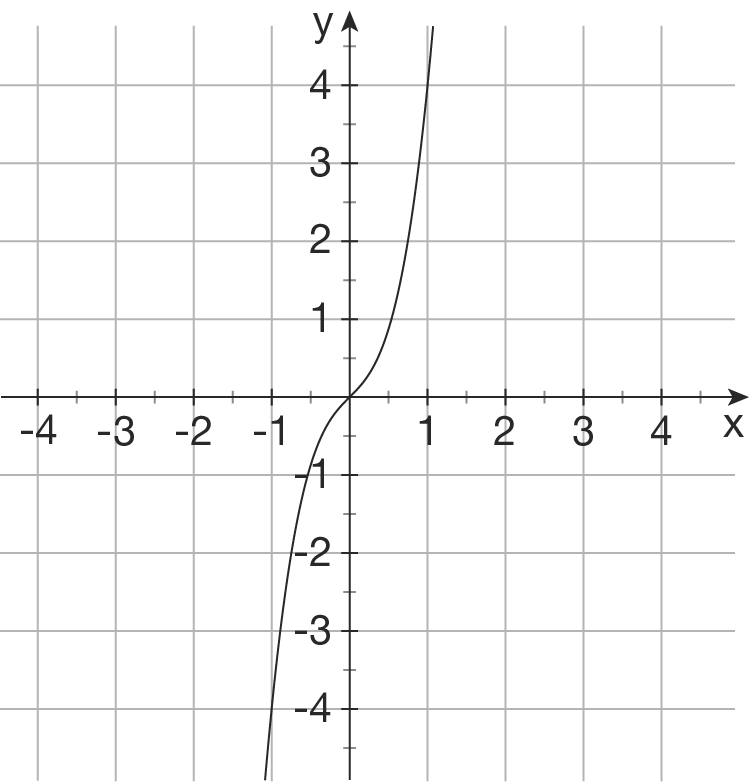

c)
Hinweis: 
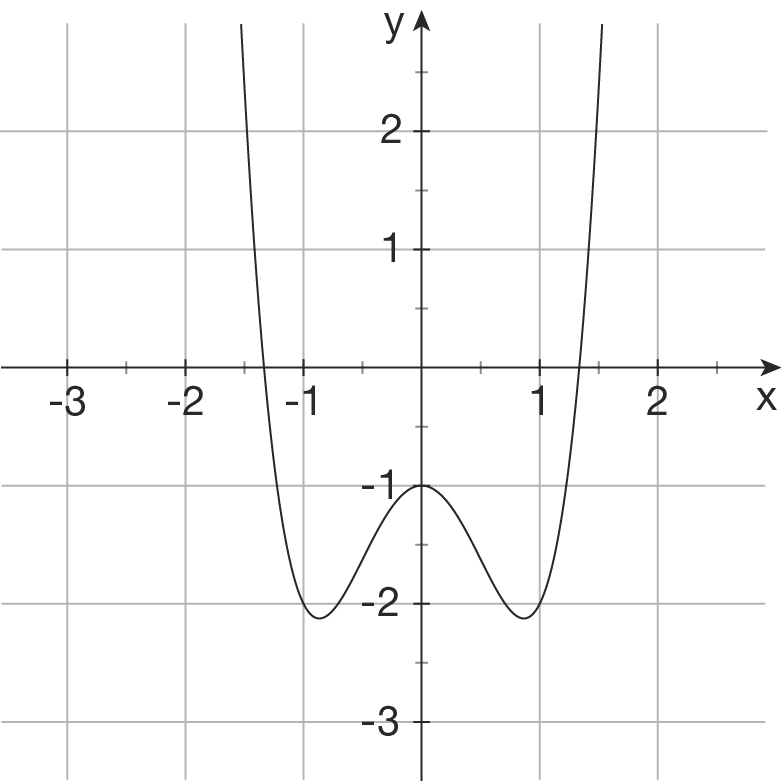

d)

e)

f)

2.
Gegeben sind die Schaubilder einiger gebrochenrationaler Funktionen. Bestimme einen möglichen Funktionsterm.



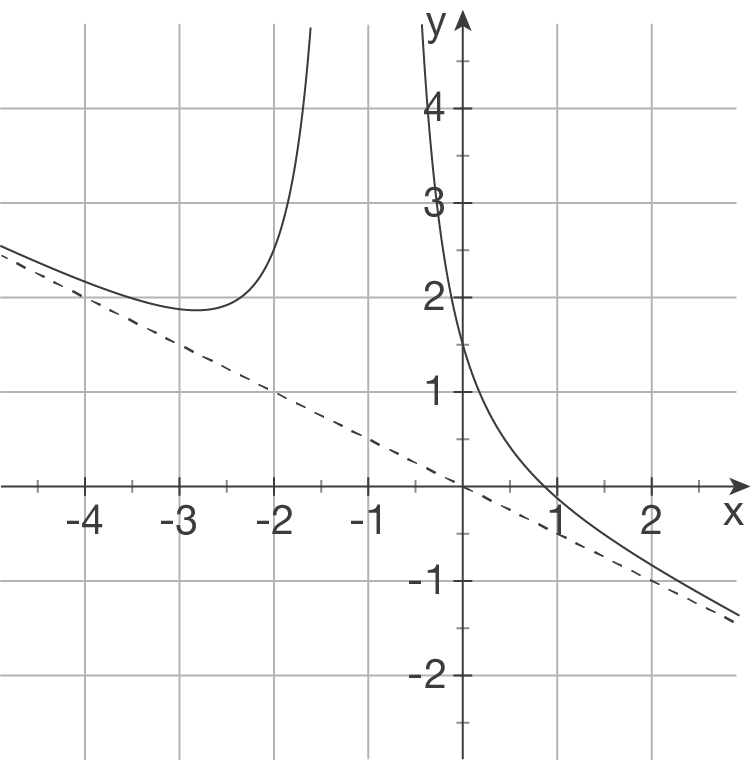
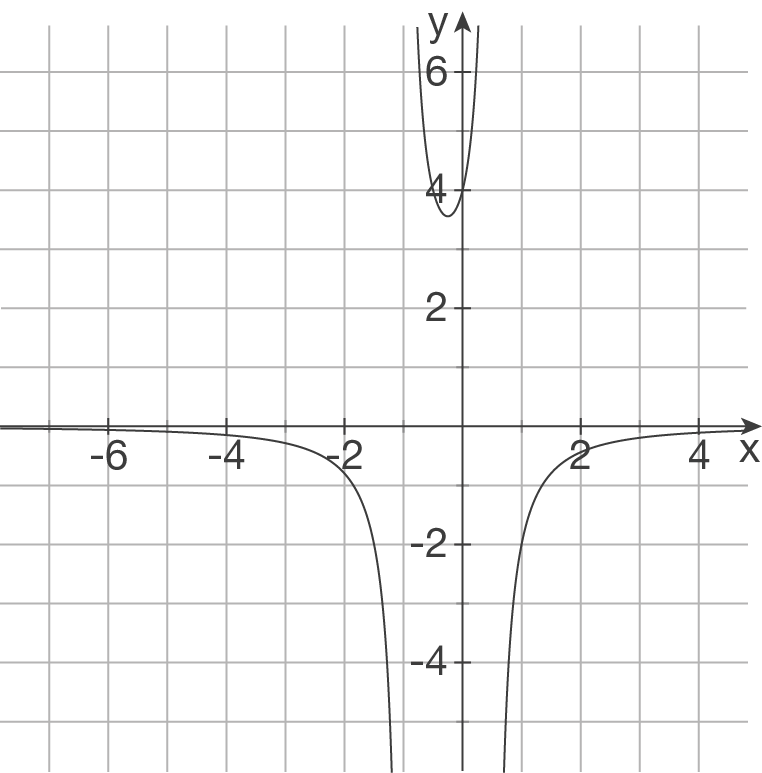
a)

b)

c)

d)
Hinweis: 
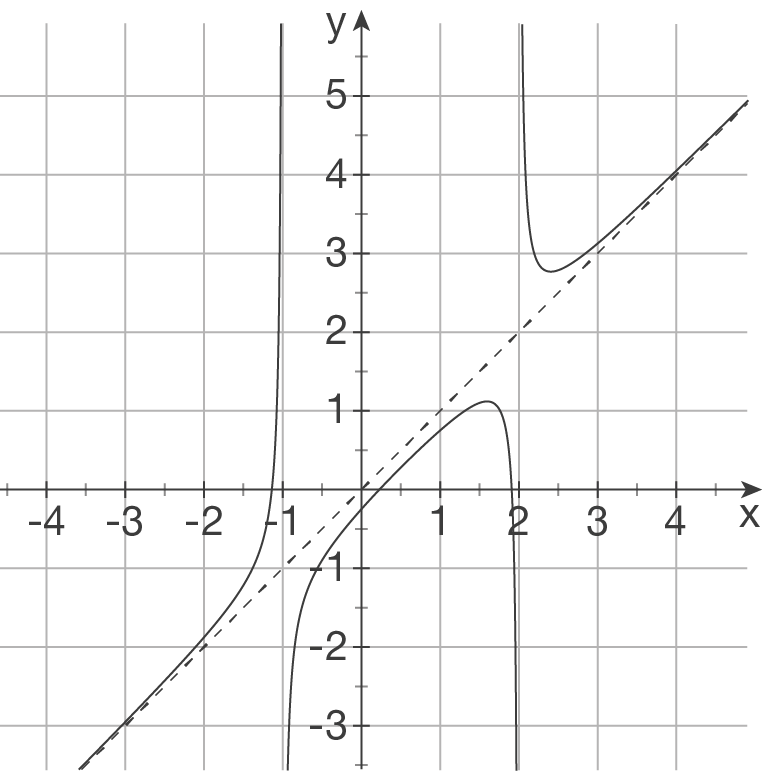

e)

f)

3.
Ordne jedem Funktionsterm ein Schaubild zu und begründe deine Entscheidung.






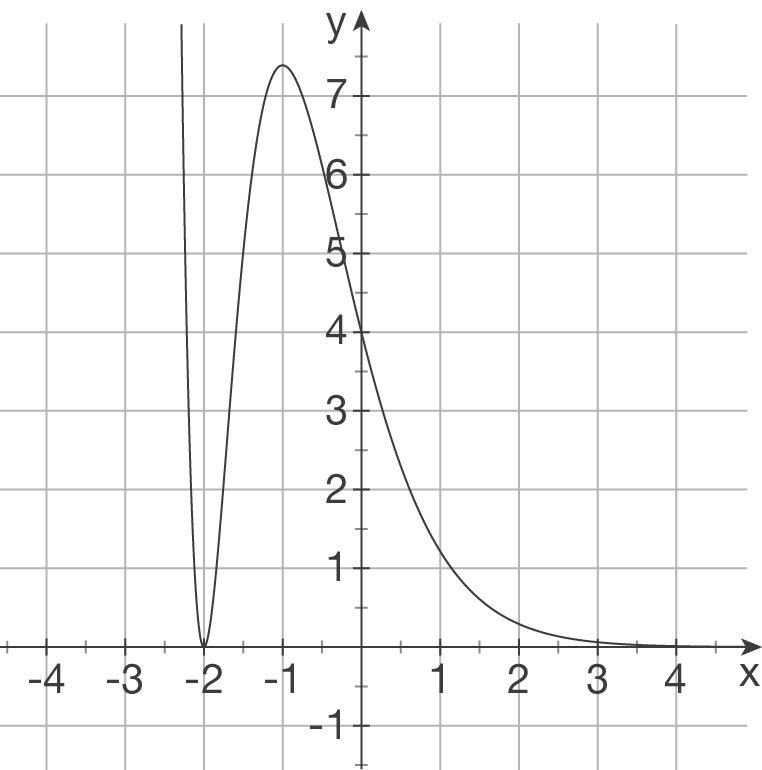
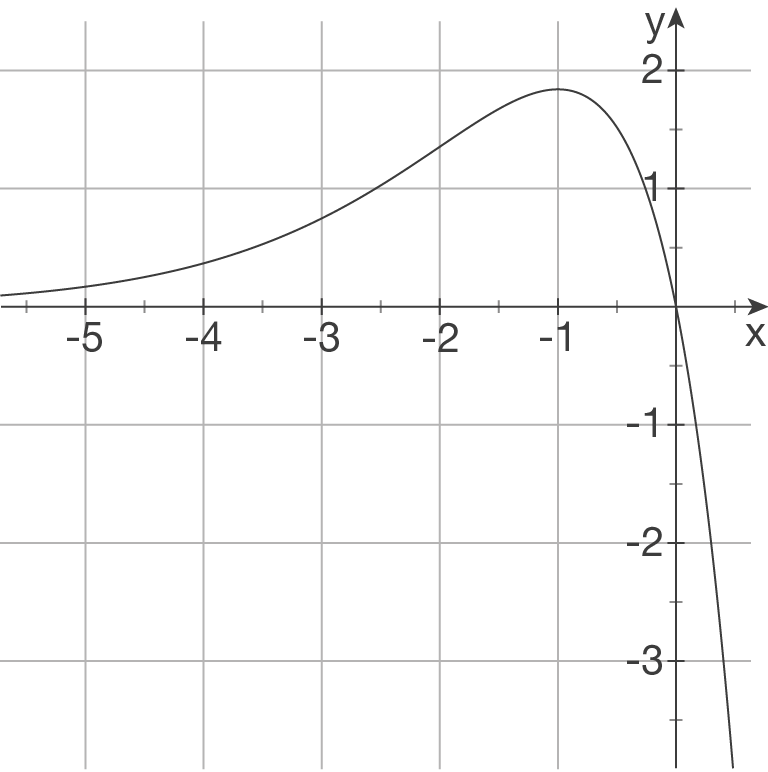
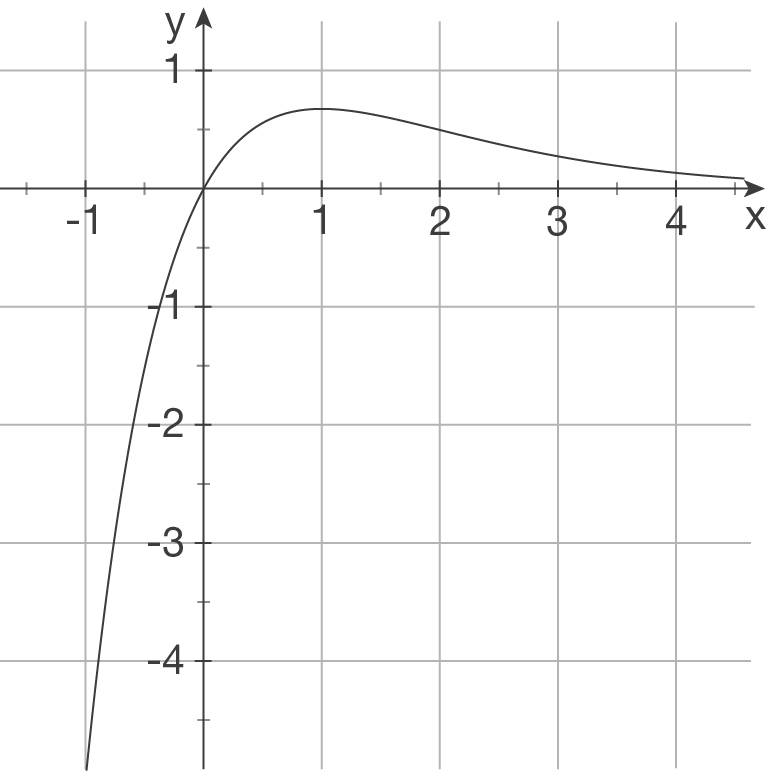
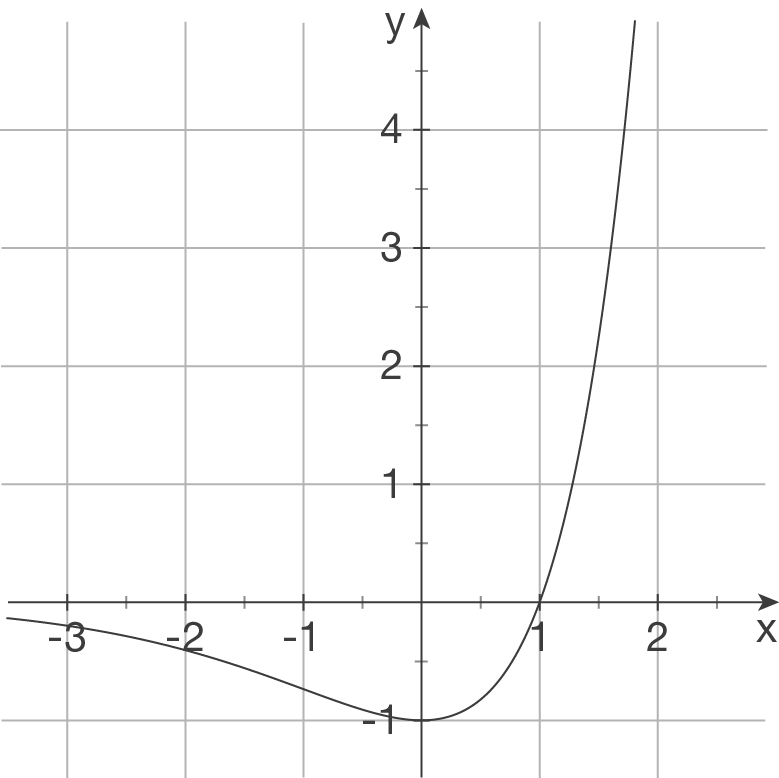
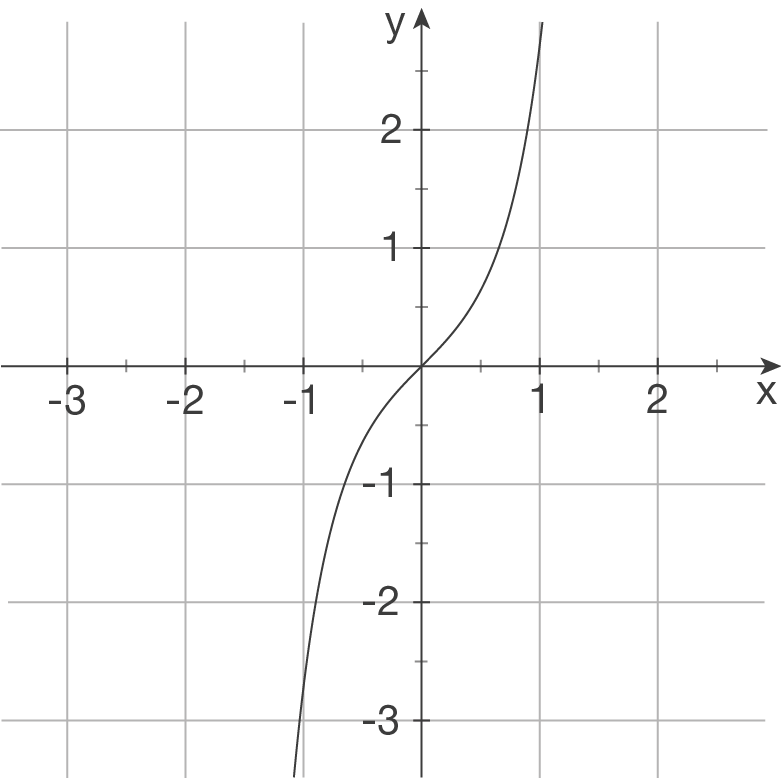

a)
b)
c)
d)
e)
f)
(1)

(2)

(3)

(4)

(5)

(6)

4.
Gegeben sind die Schaubilder einiger trigonometrischer Funktionen.
a)
Interpretiere folgende Schaubilder als Sinuskurven und bestimme einen möglichen Funktionsterm.
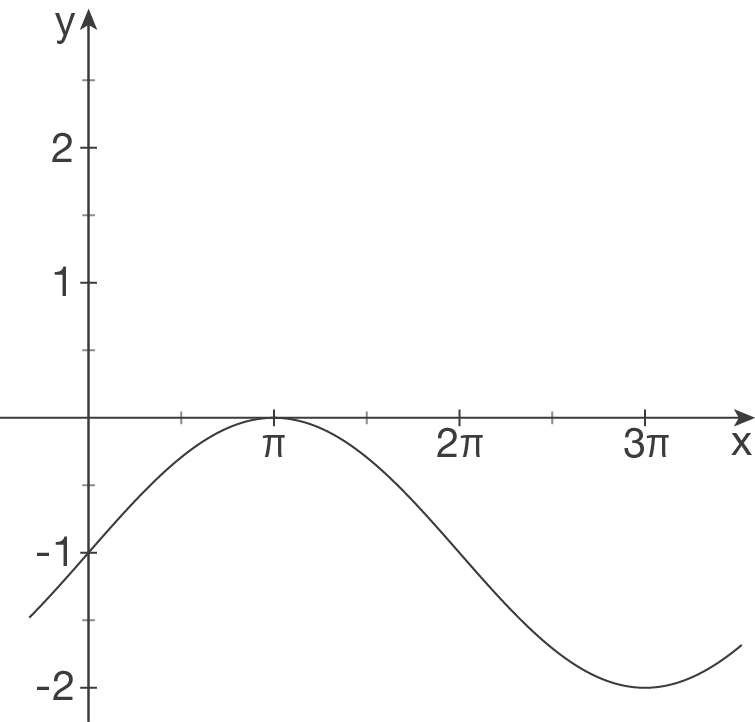
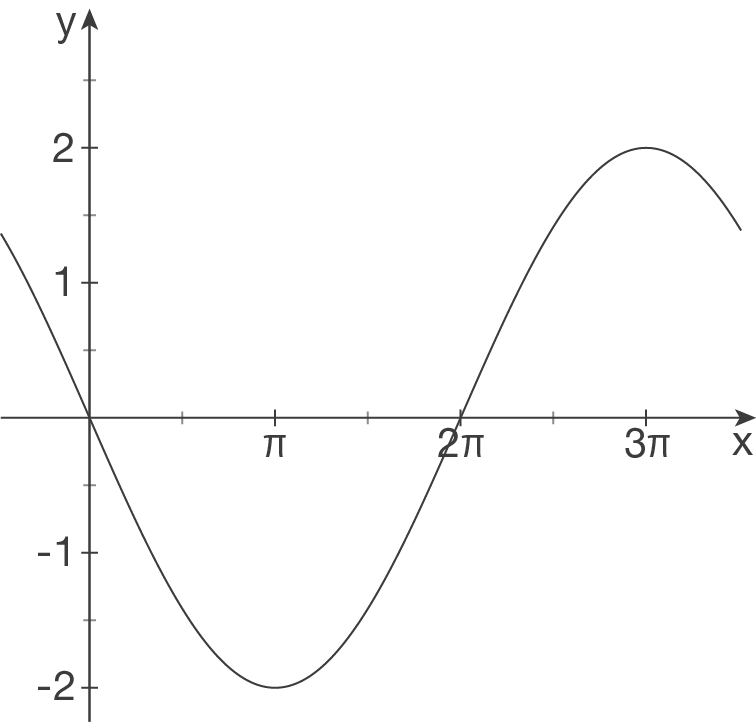
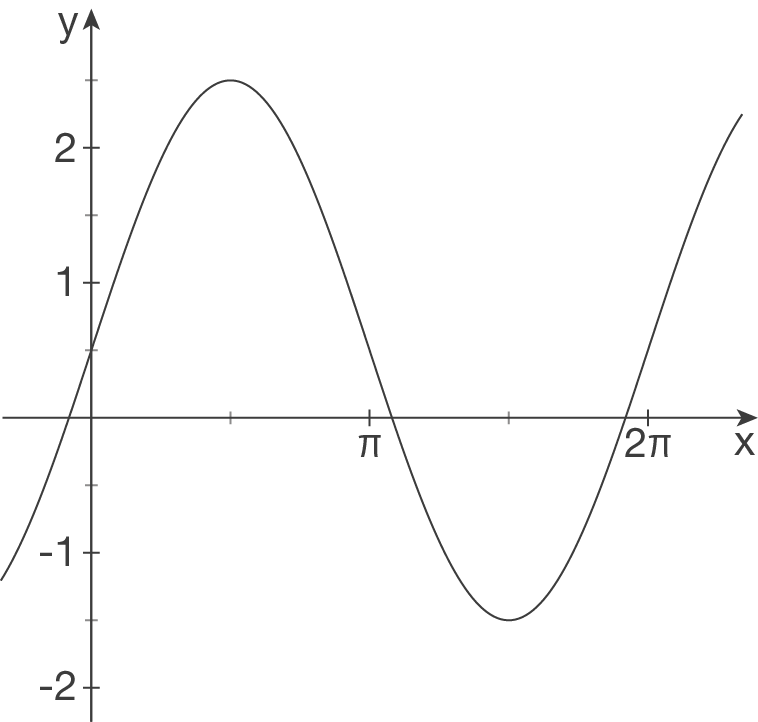
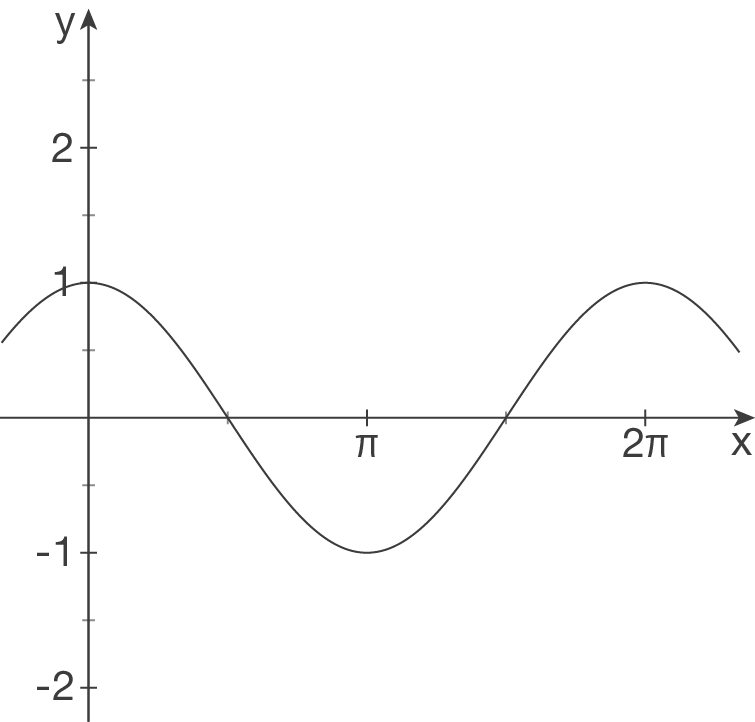
(1)

(2)

(3)

(4)

b)
Interpretiere folgende Schaubilder als Cosinuskurven und bestimme einen möglichen Funktionsterm.
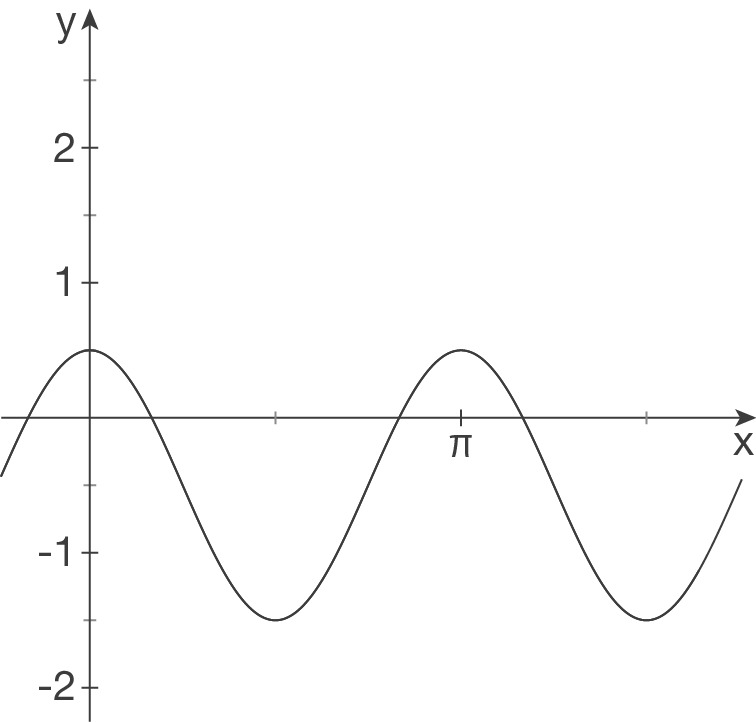
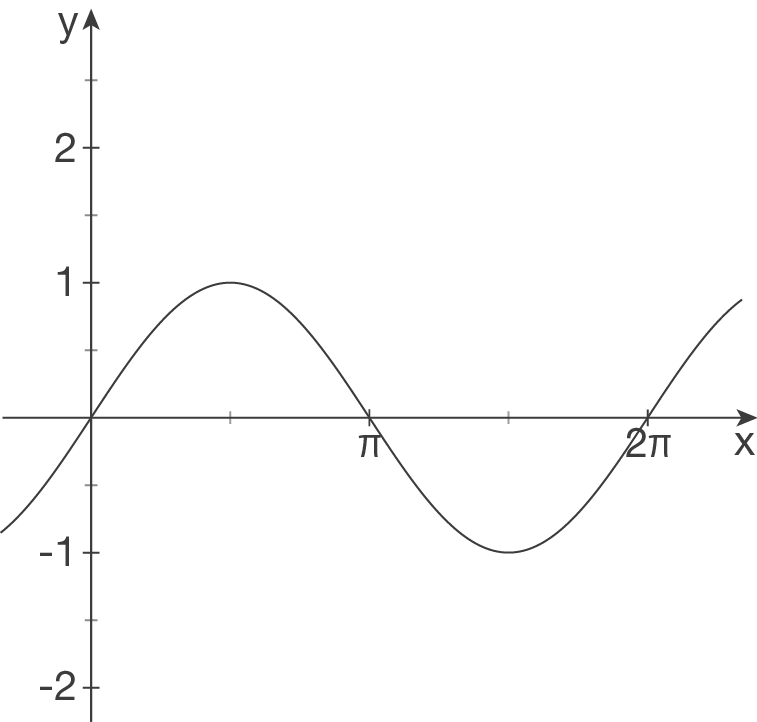
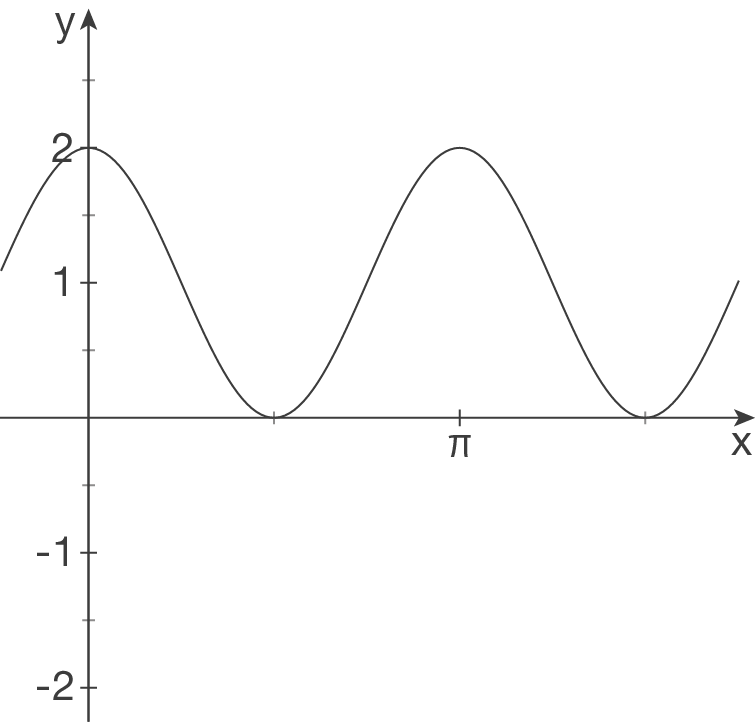
(1)

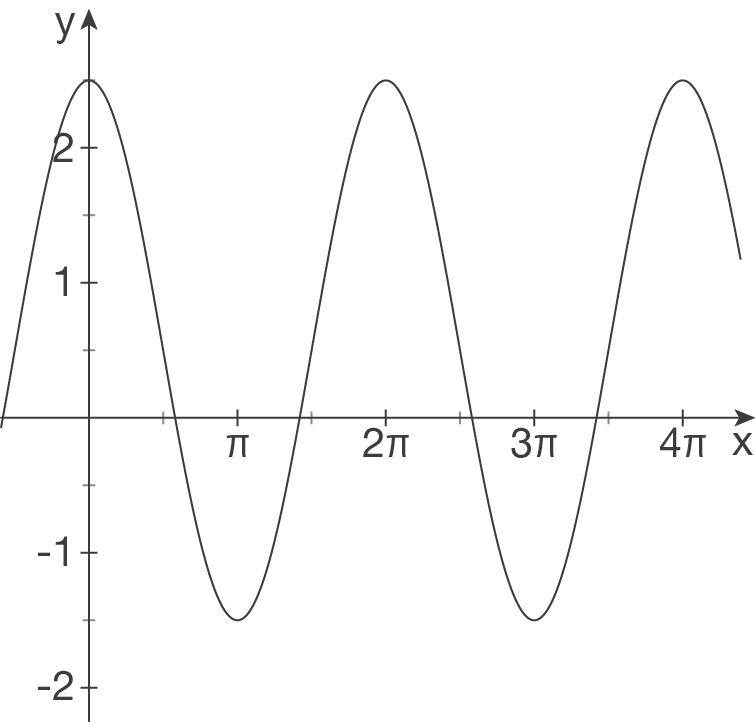
(2)

(3)

(4)

5.
Ordne jedem Funktionsterm ein Schaubild zu und begründe deine Entscheidung.




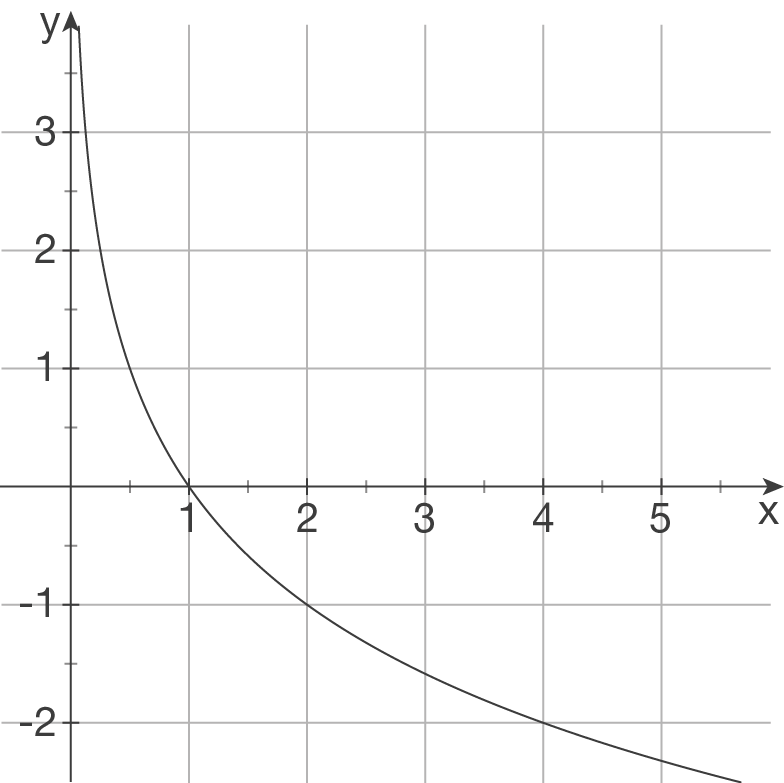
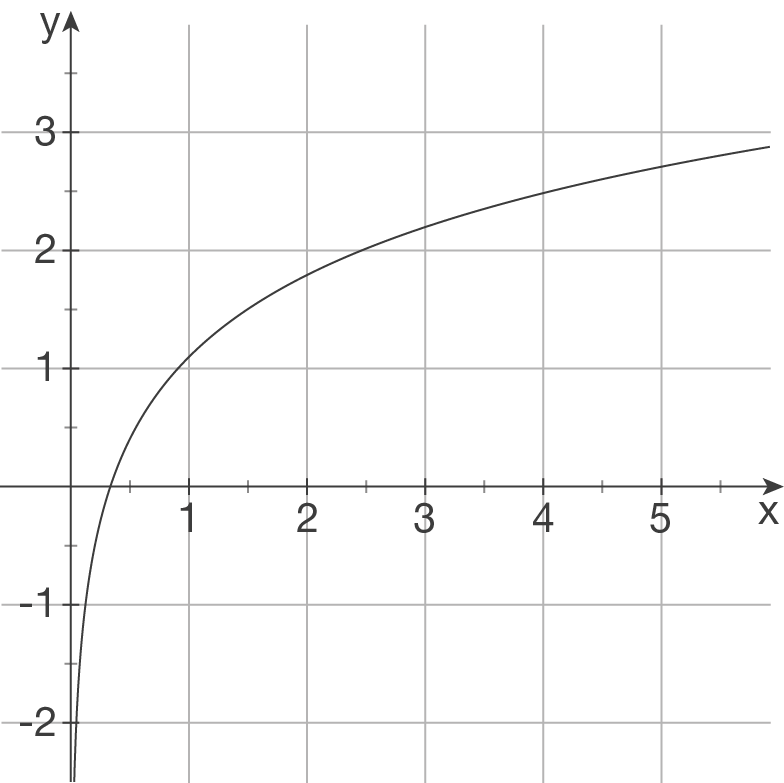
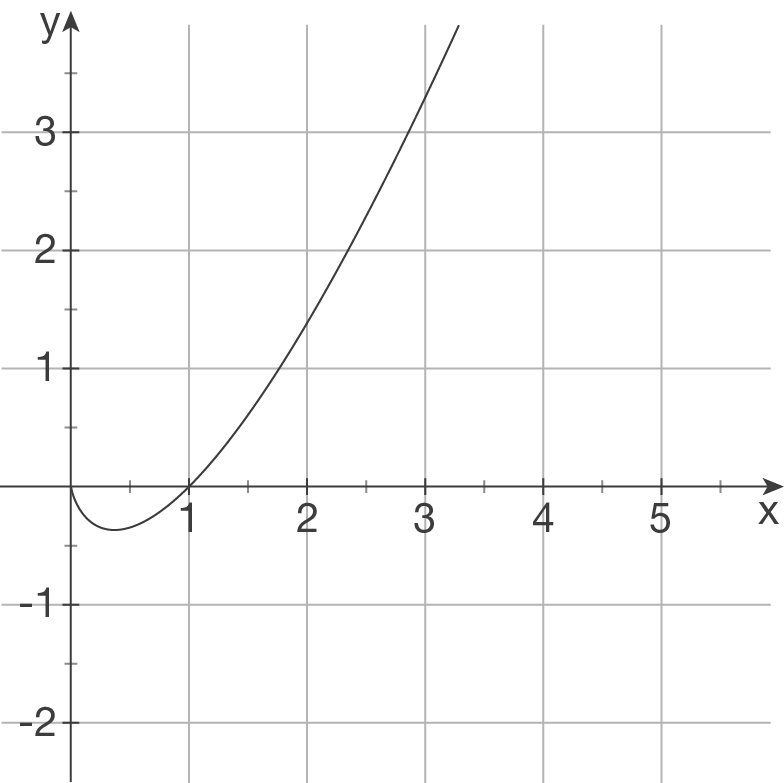
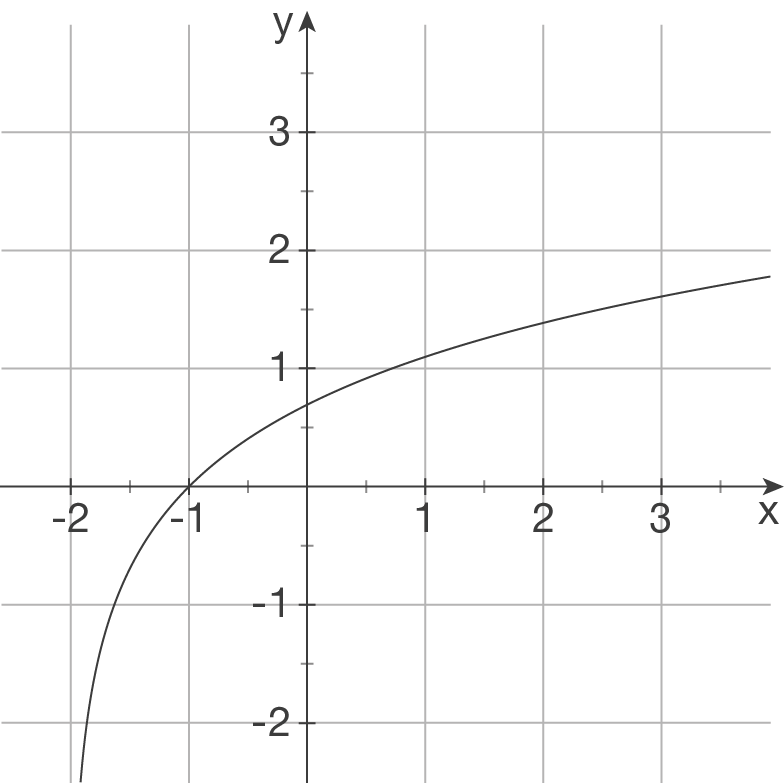
a)
b)
c)
d)
(1)

(2)

(3)

(4)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Funktionsgleichungen bestimmen
a)
Ansatz: Funktion 2. Grades mit
 .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.
 ,
,  und
und  ab.
Einsetzen in
ab.
Einsetzen in
 ergibt:
ergibt:
Setzt man  in (3a) ein,
so erhält man:
in (3a) ein,
so erhält man:
 Setzt man
Setzt man  in (2a) ein, so erhält man:
in (2a) ein, so erhält man:
 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:
 .
.
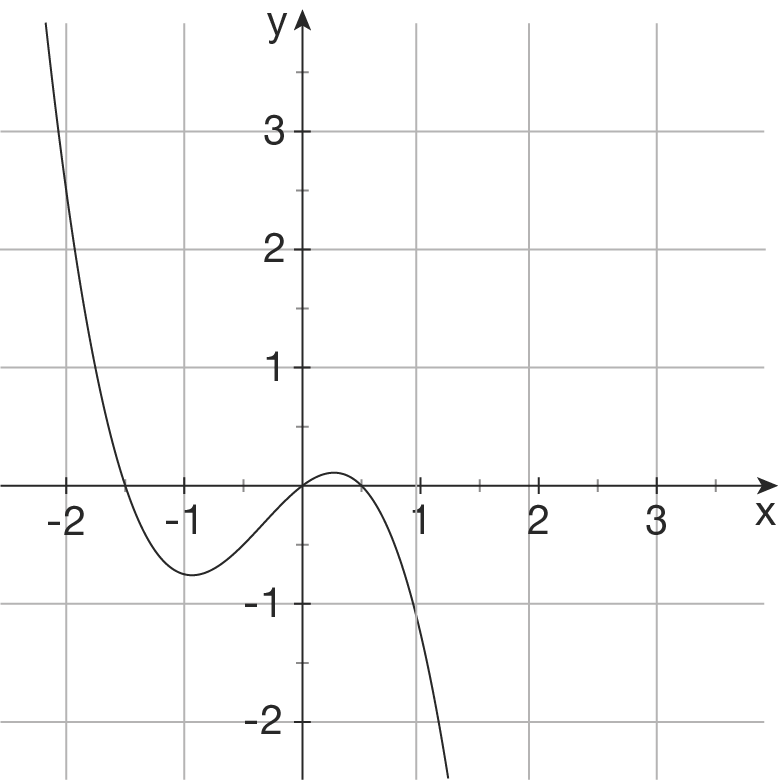
b)
Ansatz: Funktion 3. Grades, punktsymmetrisch zum Ursprung (  nur ungerade Exponenten) mit
nur ungerade Exponenten) mit  .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.  und
und  ab.
Einsetzen in
ab.
Einsetzen in  ergibt:
ergibt:
Setzt man in (1a) ein, so erhält man:
in (1a) ein, so erhält man:
 Setzt man
Setzt man  in (2a) ein,
so erhält man:
in (2a) ein,
so erhält man:
 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:
 .
.
Setzt man
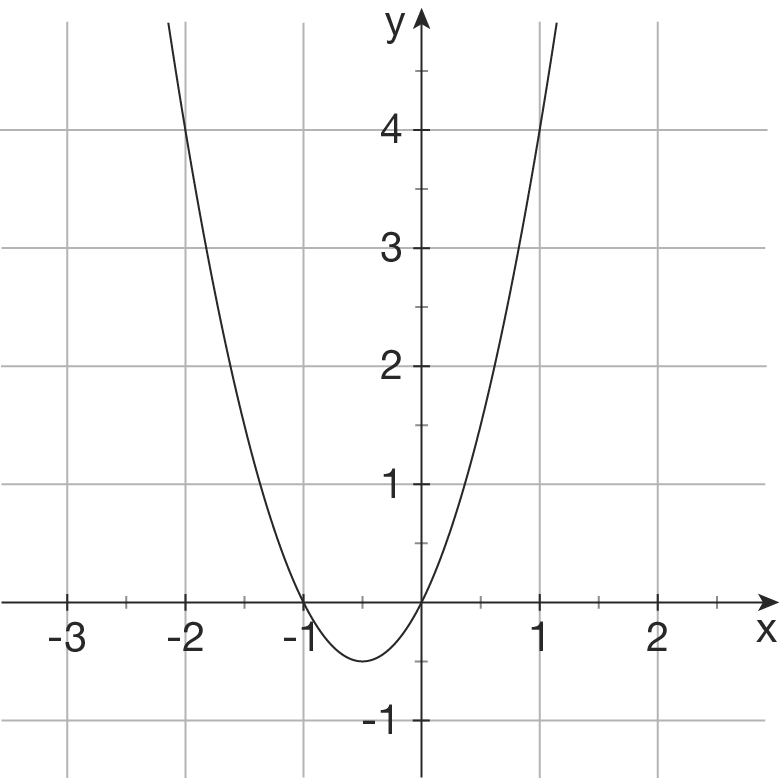
c)
Ansatz: Funktion 4. Grades, achsensymmetrisch zur x-Achse ( nur gerade Exponenten) mit
nur gerade Exponenten) mit  .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.  ,
,  und
und  ab.
Einsetzen in
ab.
Einsetzen in  ergibt:
ergibt:
Setzt man in (3a) ein, so erhält man:
in (3a) ein, so erhält man:
 Setzt man
Setzt man  in (2a) ein, so erhält man:
in (2a) ein, so erhält man:
 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:  .
.
Setzt man
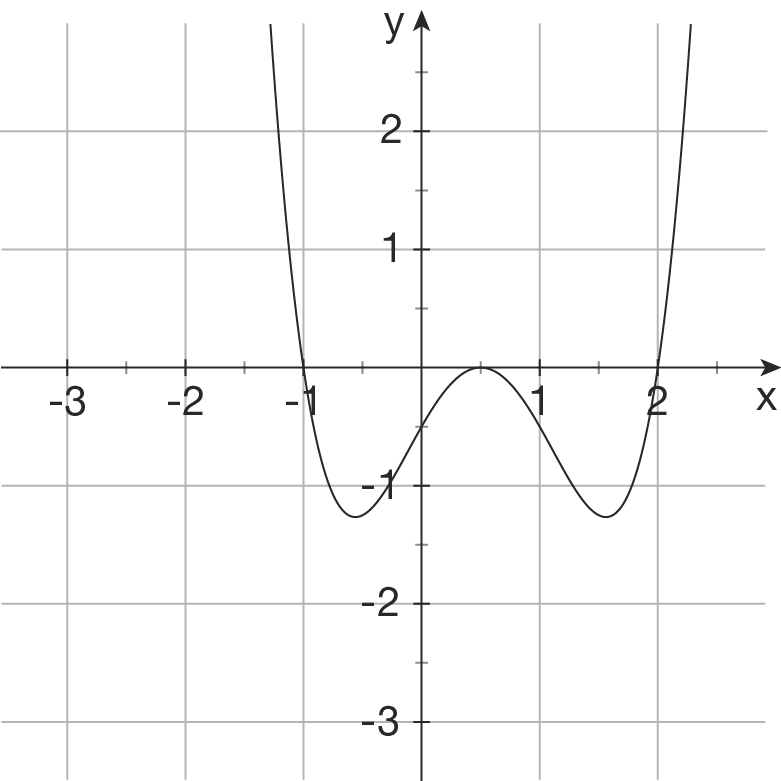
d)
Ansatz: Funktion 4. Grades mit 4 Nullstellen (eine bei  ,eine bei
,eine bei  und eine doppelte Nullstelle bei
und eine doppelte Nullstelle bei  ) und der Faktorisierung
) und der Faktorisierung
 Damit erhält man:
Damit erhält man:
Aus dem Schaubild liest man z.B. ab.
ab.
Einsetzen in den Ansatz liefert:
Die Funktionsgleichung lautet damit:
 .
.
Aus dem Schaubild liest man z.B.
Einsetzen in den Ansatz liefert:
Die Funktionsgleichung lautet damit:
e)
Ansatz: Funktion 3. Grades mit 3 Nullstellen (eine bei  , eine bei
, eine bei  und eine bei
und eine bei  ) und der Faktorisierung
) und der Faktorisierung
 .
Damit erhält man:
.
Damit erhält man:
Aus dem Schaubild liest man z.B. ab.
ab.
Einsetzen in den Ansatz liefert:
Die Funktionsgleichung lautet damit: .
.
Aus dem Schaubild liest man z.B.
Einsetzen in den Ansatz liefert:
Die Funktionsgleichung lautet damit:
f)
Ansatz: Funktion 2. Grades mit zwei Nullstellen (eine bei  und eine bei
und eine bei  ) und der Faktorisierung
) und der Faktorisierung  .
Damit erhält man:
.
Damit erhält man:
 Aus dem Schaubild liest man z.B.
Aus dem Schaubild liest man z.B.  ab.
ab.
Einsetzen in den Ansatz liefert: Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:
 .
.
Einsetzen in den Ansatz liefert:
2.
Funktionsgleichungen bestimmen
Prinzipiell braucht man bei solchen Aufgaben einen allgemeinen Ansatz. Mithilfe von Punkten, Polstellen und Asymptoten kann man dann die Funktionsgleichung näher bestimmen.
Der allgemeine Ansatz lautet
 mit
mit  falls ein VZW vorliegt und
falls ein VZW vorliegt und
 falls kein VZW vorliegt.
falls kein VZW vorliegt.
Dabei beschreibt die Verschiebung in
die Verschiebung in  -Richtung und
-Richtung und  die Verschiebung in
die Verschiebung in  -Richtung. Die Werte von
-Richtung. Die Werte von  und
und  müssen anhand von Polstellen und Asymptoten entsprechend bestimmt werden. Die Polstellen sind die Stellen, an denen der Nenner gleich Null ist. Eine Asymptote liegt vor, falls sich die Funktion für
müssen anhand von Polstellen und Asymptoten entsprechend bestimmt werden. Die Polstellen sind die Stellen, an denen der Nenner gleich Null ist. Eine Asymptote liegt vor, falls sich die Funktion für  einer Geraden (waagrechte oder schiefe Asymptote) annähert.
einer Geraden (waagrechte oder schiefe Asymptote) annähert.
Der allgemeine Ansatz lautet
Dabei beschreibt
a)
Ansatz:
 Polstelle bei
Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei
 .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.  ab. Einsetzen liefert:
ab. Einsetzen liefert:

 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:

b)
Ansatz:
 (kein VZW)
Polstelle bei
(kein VZW)
Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei
 .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.
 ab. Einsetzen liefert:
ab. Einsetzen liefert:
 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:

c)
Ansatz:
 Polstelle bei
Polstelle bei  schiefe Asymptote mit
schiefe Asymptote mit
 .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.
 ab. Einsetzen liefert:
ab. Einsetzen liefert:

 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:

d)
Ansatz:
 (zwei Polstellen)
1. Polstelle bei
(zwei Polstellen)
1. Polstelle bei  2. Polstelle bei
2. Polstelle bei  schiefe Asymptote mit
schiefe Asymptote mit
 .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.  ab. Einsetzen liefert:
ab. Einsetzen liefert:

 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:

e)
Ansatz:
 (kein VZW)
Polstelle bei
(kein VZW)
Polstelle bei  schiefe Asymptote mit
schiefe Asymptote mit
 .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.
 ab. Einsetzen liefert:
ab. Einsetzen liefert:

 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:

f)
Ansatz:
 (zwei Polstellen)
1. Polstelle bei
(zwei Polstellen)
1. Polstelle bei  2. Polstelle bei
2. Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei
 .
Aus dem Schaubild liest man z.B.
.
Aus dem Schaubild liest man z.B.
 ab. Einsetzen liefert:
ab. Einsetzen liefert:

 Die Funktionsgleichung lautet damit:
Die Funktionsgleichung lautet damit:

3.
Funktionsgleichungen zuordnen

 (5)
Begründung:
(5)
Begründung:
 .
.

 (4)
Begründung:
(4)
Begründung:
 hat als einzige der sechs Funktionen eine Nullstelle bei
hat als einzige der sechs Funktionen eine Nullstelle bei  .
.

 (6)
Begründung:
(6)
Begründung:

 .
.

 (3)
Begründung:
(3)
Begründung:

 und (5) ist bereits zugeordnet.
und (5) ist bereits zugeordnet.

 (2)
Begründung:
(2)
Begründung:
 und
und  hat eine Nullstelle bei
hat eine Nullstelle bei  .
.

 (1)
Begründung:
(1)
Begründung:
 hat als einzige der sechs Funktionen eine Nullstelle bei
hat als einzige der sechs Funktionen eine Nullstelle bei  .
.
a)
b)
c)
d)
e)
f)
4.
Funktionsgleichungen bestimmen
a)
Für diesen Typ von Aufgaben gibt es einen generellen Ansatz:
 (
( ).
Dabei beschreibt
).
Dabei beschreibt
a die Streckung in  -Richtung,
-Richtung,
b die Streckung in  -Richtung
-Richtung
 Abstand zwischen zwei Extrema,
Abstand zwischen zwei Extrema,
 ,
,
c die Verschiebung in  -Richtung,
-Richtung,
d die Verschiebung in  -Richtung.
Für den Fall
-Richtung.
Für den Fall  beschreibt
beschreibt  die Streckung in
die Streckung in  -Richtung und die gesamte Funktion ist mit
-Richtung und die gesamte Funktion ist mit  in
in  -Richtung verschoben.
(1) Verschiebung in
-Richtung verschoben.
(1) Verschiebung in  -Richtung:
-Richtung:
 .
Streckung in
.
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , allerdings ist die Funktion um 1 nach unten verschoben. Daher ist
, allerdings ist die Funktion um 1 nach unten verschoben. Daher ist  .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander, daher ist
auseinander, daher ist  .
Verschiebung in
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Die Funktionsgleichung lautet damit:
.
Die Funktionsgleichung lautet damit:
 .
(2) Verschiebung in
.
(2) Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Streckung in
.
Streckung in  -Richtung:
Tiefpunkt liegt bei
-Richtung:
Tiefpunkt liegt bei  , daher ist
, daher ist
 .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander, daher ist
auseinander, daher ist
 .
Verschiebung in
.
Verschiebung in  -Richtung:
Da an der Stelle
-Richtung:
Da an der Stelle  ein Tiefpunkt vorliegt, ist die Funktion um
ein Tiefpunkt vorliegt, ist die Funktion um  in
in  -Richtung verschoben.
Die Funktionsgleichung lautet damit:
-Richtung verschoben.
Die Funktionsgleichung lautet damit:
 .
(3) Verschiebung in
.
(3) Verschiebung in  -Richtung:
-Richtung:
 .
Streckung in
.
Streckung in  -Richtung:
Der Funktionswert des Maximums ist
-Richtung:
Der Funktionswert des Maximums ist  . Da die Funktion aber um
. Da die Funktion aber um  nach oben verschoben ist, gilt
nach oben verschoben ist, gilt
 .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander,
daher ist
auseinander,
daher ist  .
Verschiebung in
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Die Funktionsgleichung lautet damit:
.
Die Funktionsgleichung lautet damit:
 .
(4) Verschiebung in
.
(4) Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Streckung in
.
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , daher ist
, daher ist  .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander,
daher ist
auseinander,
daher ist  .
Verschiebung in
.
Verschiebung in  -Richtung:
Da an der Stelle
-Richtung:
Da an der Stelle  ein Hochpunkt vorliegt ist die Funktion um
ein Hochpunkt vorliegt ist die Funktion um  in
in  -Richtung verschoben.
Die Funktionsgleichung lautet damit:
-Richtung verschoben.
Die Funktionsgleichung lautet damit:
 .
.
b)
Für diesen Typ von Aufgaben gibt es einen generellen Ansatz:
 (
( ).
Dabei beschreibt
).
Dabei beschreibt
a die Streckung in  -Richtung,
-Richtung,
b die Streckung in  -Richtung
-Richtung
 Abstand zwischen zwei Extrema,
Abstand zwischen zwei Extrema,
 ,
,
c die Verschiebung in  -Richtung,
-Richtung,
d die Verschiebung in  -Richtung.
-Richtung.
Für den Fall  beschreibt
beschreibt  die Streckung in
die Streckung in  -Richtung und die gesamte Funktion ist mit
-Richtung und die gesamte Funktion ist mit  in
in  -Richtung verschoben.
(1) Verschiebung in
-Richtung verschoben.
(1) Verschiebung in  -Richtung:
-Richtung:  .
Streckung in
.
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , da die Funktion jedoch um
, da die Funktion jedoch um  nach unten verschoben ist, ist
nach unten verschoben ist, ist  .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander,
daher ist
auseinander,
daher ist  .
Verschiebung in
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Die Funktionsgleichung lautet damit:
.
Die Funktionsgleichung lautet damit:
 .
(2) Verschiebung in
.
(2) Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Streckung in
.
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , daher ist
, daher ist  .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander,
daher ist
auseinander,
daher ist  .
Verschiebung in
.
Verschiebung in  -Richtung:
-Richtung:
 .
Die Funktionsgleichung lautet damit:
.
Die Funktionsgleichung lautet damit:  .
(3) Verschiebung in
.
(3) Verschiebung in  -Richtung:
-Richtung:
 .
Streckung in
.
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , da die Funktion jedoch um 1 nach oben verschoben ist erhält man:
, da die Funktion jedoch um 1 nach oben verschoben ist erhält man:
 .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander,
daher ist
auseinander,
daher ist  .
Verschiebung in
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Die Funktionsgleichung lautet damit:
.
Die Funktionsgleichung lautet damit:
 .
(4) Verschiebung in
.
(4) Verschiebung in  -Richtung:
-Richtung:
 .
Streckung in
.
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , da die Funktion jedoch um
, da die Funktion jedoch um  nach oben verschoben ist erhält man:
nach oben verschoben ist erhält man:
 .
Streckung in
.
Streckung in  -Richtung:
Extrema liegen um
-Richtung:
Extrema liegen um  auseinander,
daher ist
auseinander,
daher ist  .
Verschiebung in
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Die Funktionsgleichung lautet damit:
.
Die Funktionsgleichung lautet damit:
 .
.
5.
Funktionsgleichungen zuordnen

 (3)
Begründung:
(3)
Begründung:


 (1)
Begründung:
(1)
Begründung:



 (4)
Begründung:
(4)
Begründung:
 hat als einzige der vier Funktionen eine Nullstelle bei
hat als einzige der vier Funktionen eine Nullstelle bei  .
.

 (2)
Begründung:
(2)
Begründung:

a)
b)
c)
d)