Trigonometrische Funktionen
Trigonometrische Funktionen sind beispielsweise Funktionen der Form

 Dass es sich um eine trigonometrische Funktion handelt, kannst du vor allem daran erkennen, wenn der Graph periodisch verläuft.
Dass es sich um eine trigonometrische Funktion handelt, kannst du vor allem daran erkennen, wenn der Graph periodisch verläuft.
Ist nicht vorgegeben, ob es sich um eine - oder
- oder  -Funktion handelt, so kannst du die Stelle
-Funktion handelt, so kannst du die Stelle  betrachten:
betrachten:
Ist nicht vorgegeben, ob es sich um eine
- Liegt hier ein Hochpunkt, dann wähle
als Ausgangsfunktion
- Liegt hier ein Wendepunkt, dann wähle
als Ausgangsfunktion
- Sonst lege selbst fest, ob du von
oder
ausgehen möchtest
- Lies die Amplitude
ab: Dies ist die halbe Differenz der
-Koordinaten der Hoch- und Tiefpunkte
- Lies die Periodenlänge
ab: Dies ist die Differnz zwischen zwei Hoch- bzw. Tiefpunkten. Daraus erhältst du dann
- Falls kein Hoch- oder Wendepunkt bei
liegt, bestimme die Phasenverschiebung
, also die Verschiebung entlang der
-Achse, indem du nach dem nächsten Hoch- oder Wendepunkt suchst und die Distanz zum Urprung abliest.
- Bestimme gegebenenfalls die Verschiebung entlang der
-Achse
- Setze diese Werte in die allgemeine Funktionsgleichung ein
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Für diesen Typ von Aufgaben gibt es zwei generelle Ansätze:
 die Streckung in
die Streckung in  -Richtung.
-Richtung.
 die die Periodenlänge
die die Periodenlänge  (Abstand zwischen zwei Hoch- bzw. Tiefpunkten) . Berechne
(Abstand zwischen zwei Hoch- bzw. Tiefpunkten) . Berechne  mit
mit 
 die Verschiebung in
die Verschiebung in  -Richtung. Für
-Richtung. Für  wird der Graph nach rechts und für
wird der Graph nach rechts und für  nach links verschoben.
nach links verschoben.
 die Verschiebung in
die Verschiebung in  -Richtung.
-Richtung.
 Streckung in
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , daher ist
, daher ist  .
.
Streckung in  -Richtung:
Im Schuabild ist gerade so eine Periode zu erkennen, diese beginnt bei
-Richtung:
Im Schuabild ist gerade so eine Periode zu erkennen, diese beginnt bei  und endet bei
und endet bei  . Für
. Für  gilt also
gilt also  .
.
Verschiebung in  -Richtung:
Im Ursprung befindet sich eine Nullstelle. Somit gibt es keine Verschiebung,
-Richtung:
Im Ursprung befindet sich eine Nullstelle. Somit gibt es keine Verschiebung,  .
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Funktionsterm:
.
Funktionsterm: 
 Streckung in
Streckung in  -Richtung:
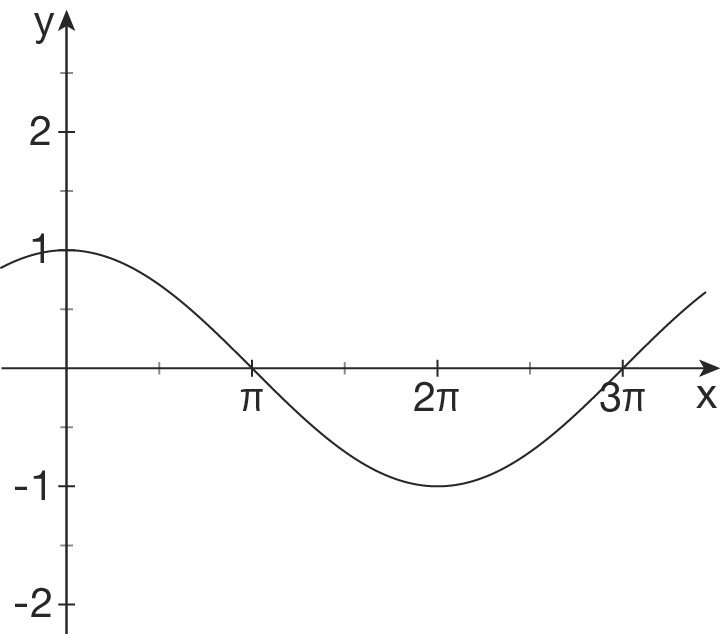
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , daher ist
, daher ist  .
.
Streckung in  -Richtung:
Hier ist keine ganze PEriode zu erkennen. Schau dir deshalb die Länge einer halben Periode an. Die ist vom Hochpunkt bei
-Richtung:
Hier ist keine ganze PEriode zu erkennen. Schau dir deshalb die Länge einer halben Periode an. Die ist vom Hochpunkt bei  bis zum Tiefpunkt bei
bis zum Tiefpunkt bei  . Eine ganze Periode ist also
. Eine ganze Periode ist also  , daher ist
, daher ist  .
.
Verschiebung in  -Richtung:
Da der Kosinus mit einem Hochpunkt im Ursprung beginnt gibt es keine Verschiebung,
-Richtung:
Da der Kosinus mit einem Hochpunkt im Ursprung beginnt gibt es keine Verschiebung,  .
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Funktionsterm:
.
Funktionsterm:

 Streckung in
Streckung in  -Richtung:
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , daher ist
, daher ist  .
.
Streckung in  -Richtung:
Eine Periode ist hier
-Richtung:
Eine Periode ist hier  , somit gilt
, somit gilt  .
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Funktionsterm:
.
Funktionsterm:

 Streckung in
Streckung in  -Richtung:
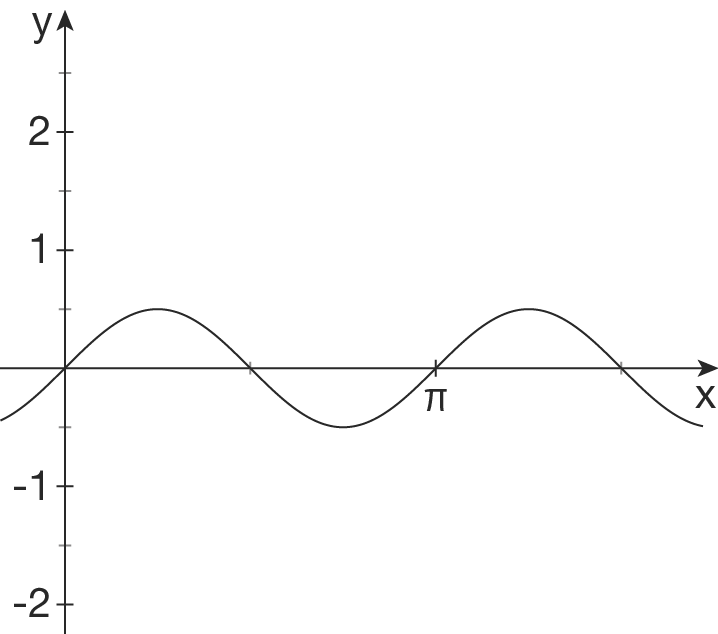
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , daher ist
, daher ist  .
.
Streckung in  -Richtung:
Die Periodenlänge ist
-Richtung:
Die Periodenlänge ist  , da die beiden Nullstellen genau um
, da die beiden Nullstellen genau um  auseinander liegen. Daher ist
auseinander liegen. Daher ist  .
.
Verschiebung in  -Richtung:
Bei einem normalen Kosinus würdest du an der Stelle
-Richtung:
Bei einem normalen Kosinus würdest du an der Stelle  keinen Hochpunkt erwarten. Dies ist hier nicht der Fall, weshalb eine Verschiebung vorliegt. Suche nach dem nächsten Hochpunkt, dieser liegt bei
keinen Hochpunkt erwarten. Dies ist hier nicht der Fall, weshalb eine Verschiebung vorliegt. Suche nach dem nächsten Hochpunkt, dieser liegt bei  . Also ist der Graph im Vergleich zum normalen Kosinus um
. Also ist der Graph im Vergleich zum normalen Kosinus um  nach rechts verschoben, deshalb ist
nach rechts verschoben, deshalb ist  .
.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Funktionsterm:
.
Funktionsterm:

 Streckung in
Streckung in  -Richtung:
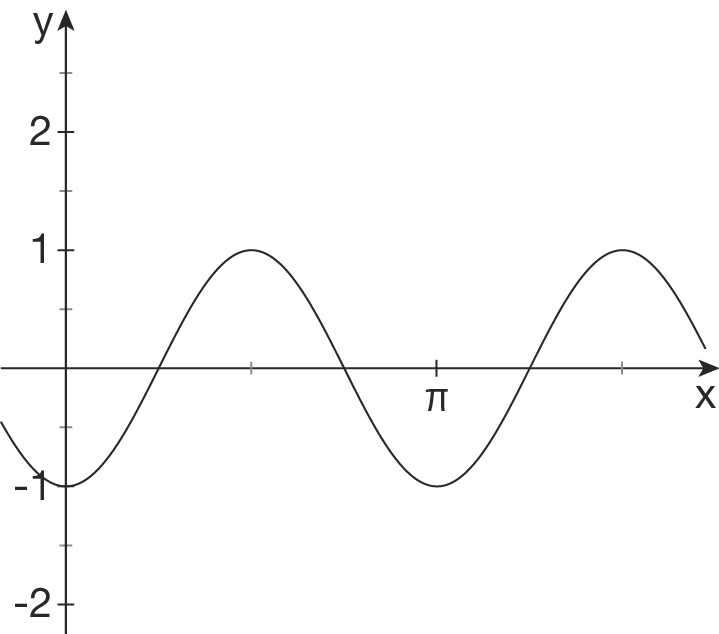
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  , daher ist
, daher ist  .
.
Streckung in  -Richtung:
Hier kannst du auch nur eine halbe Periodenlänge ablesen mit
-Richtung:
Hier kannst du auch nur eine halbe Periodenlänge ablesen mit  . Für
. Für  gilt dann
gilt dann  .
.
Verschiebung in  -Richtung:
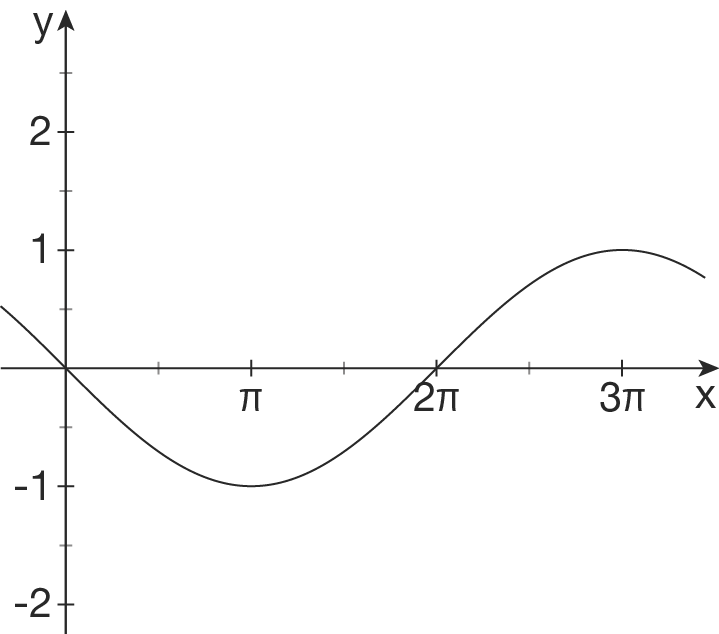
Bei einem normalen Sinus würdest du an der Stelle
-Richtung:
Bei einem normalen Sinus würdest du an der Stelle  ein Vorzeichenwechsel von
ein Vorzeichenwechsel von  nach
nach  erwarten. Dies ist hier nicht der Fall, da der Vorzeichenwechsel von
erwarten. Dies ist hier nicht der Fall, da der Vorzeichenwechsel von  nach
nach  verläuft. Suche also die Nullstelle des Graphen mit dem gewünschten Vorzeichenwechsel. Diese findest du bei
verläuft. Suche also die Nullstelle des Graphen mit dem gewünschten Vorzeichenwechsel. Diese findest du bei  , also um
, also um  nach rechts verschoben.
nach rechts verschoben.
Alternativ kannst du sagen, dass dies ein an der -Achse gespiegelter Sinus ist und ein
-Achse gespiegelter Sinus ist und ein  vor die Funktion schreiben.
vor die Funktion schreiben.
Verschiebung in  -Richtung:
keine,
-Richtung:
keine,  .
Funktionsterm:
.
Funktionsterm:
 Oder alternativ:
Oder alternativ:

 Streckung in
Streckung in  -Richtung:
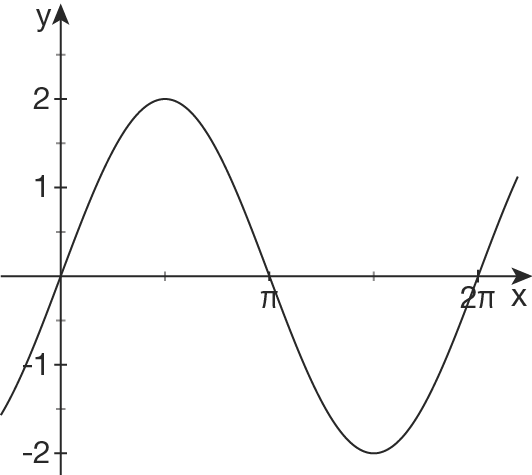
Hochpunkt liegt bei
-Richtung:
Hochpunkt liegt bei  und der Tiefpunkt bei
und der Tiefpunkt bei  . Die Höhendifferenz ist also
. Die Höhendifferenz ist also  .
.  entspriciht gerade der halben Höhendifferenz
entspriciht gerade der halben Höhendifferenz  .
.
Streckung in  -Richtung:
Du kannst eine halbe Periode ablesen, idem du die Distanz zwischen Hoch- und Tiefpunkt abliest. Es gilt
-Richtung:
Du kannst eine halbe Periode ablesen, idem du die Distanz zwischen Hoch- und Tiefpunkt abliest. Es gilt  und somit
und somit  .
.
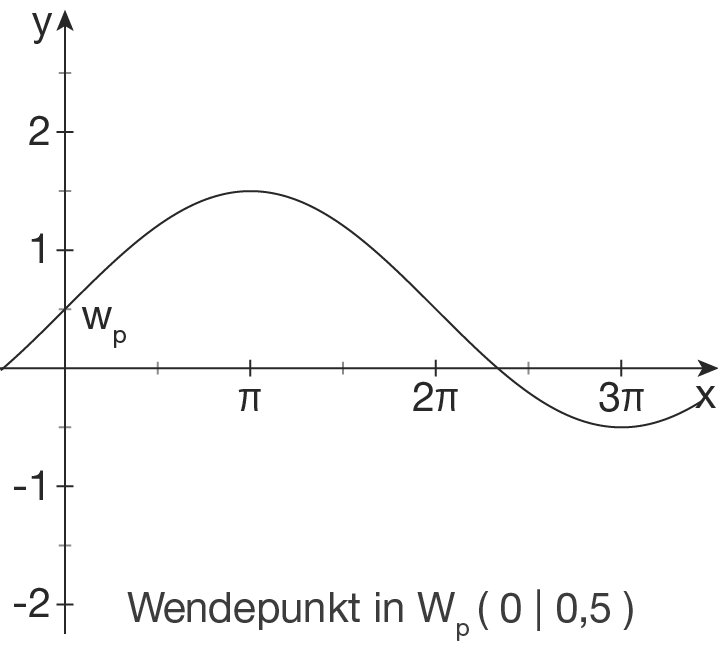
Verschiebung in  -Richtung:
Da an der Stelle
-Richtung:
Da an der Stelle  ein Wendepunkt mit positiver Steigung liegt, ist
ein Wendepunkt mit positiver Steigung liegt, ist  .
.
Verschiebung in  -Richtung:
-Richtung:
 .
Funktionsterm:
.
Funktionsterm:

- falls an der Stelle
ein Wendepunkt mit VZW von
nach
ist.
- falls an der Stelle
ein Hochpunkt ist.
1.
a)
b)
c)
d)
e)
Alternativ kannst du sagen, dass dies ein an der
f)