Abhängigkeit und Unabhängigkeit

Zwei Ereignisse $A$ und $B$ heißen stochastisch unabhängig, wenn das Eintreten des einen Ereignisses das Eintreten oder Nichteintreten des anderen Ereignisses nicht beeinflusst.
Ist dies nicht der Fall, so nennt man die beiden Ereignisse stochastisch abhängig. Oft wird auch nur kurz „unabhängig“ bzw. „abhängig“ gesagt. In Formeln bedeutet dies:

$A$ und $B$ sind unabhängig genau dann, wenn $P_A(B) = P(B)$ und $P_B(A) = P(A)$ bzw. $P(A\cap B) = P(A)\cdot P(B)$

Beispiele

Die Ergebnisse zweier Münzwürfe sind unabhängig voneinander
Beim Ziehen ohne Zurücklegen sind die Ergebnisse abhängig davon welche Kugeln schon gezogen wurden, da sich dadurch die Wahrscheinlichkeiten ändern.
Beim Ziehen mit Zurücklegen sind die Ergebnisse unabhängig davon welche Kugeln vorher gezogen wurden, da in jedem Durchgang wieder die gleichen Wahrscheinlichkeiten gelten.

Gegeben sind zwei stochastisch unabhängige Ereignisse $A$ und $B$ . Es gelte $P(A)=0,4$ und $P(B)=0,7$ . Bestimme $P(A\cap B)$ .

In einer Urne sind 5 rote Kugeln und 3 schwarze Kugeln. Die Kugeln werden einmal mit und einmal ohne Zurücklegen gezogen. Erkläre anhand dieser Zufallsexperimente stochastische Abhängigkeit und Unabhängigkeit.

$A$ und $B$ seien stochastisch unabhängig, es gelte $P(A)=0,4$ . Die Wahrscheinlichkeit für das gleichzeitige Eintreten von $A$ und $B$ beträgt 0,1. Wie groß ist $P(B)$ ?

Bei einer Umfrage in der Hamburger Fußgängerzone wurde der Bekanntheitsgrad von Stefan Raab ermittelt. $\small{16\,\%}$ der Befragten waren Männer, die Stefan Raab nicht kannten. In der Umfrage waren insgesamt $\small{52\,\%}$ Frauen.

Aus der Menge der Befragten wird nun zufällig eine Person ausgewählt. Man geht davon aus, dass die beiden Ereignisse $M$ : „Die Person ist ein Mann“ und $B$ : „Die Person kennt Stefan Raab“ stochastisch unabhängig sind. Die Wahrscheinlichkeit von $B$ ist der Bekanntheitsgrad von Stefan Raab.

Bestimme diesen in dieser Umfrage.

Würde die Umfrage einen kleineren, größeren oder einen gleich großen Bekanntheitsgrad liefern, wenn der Anteil der Frauen kleiner als $\small{52\,\%}$ wäre und wieder $\small{16\,\%}$ aller Befragten Männer sind, die Stefan Raab nicht kennen?

Begründe deine Antwort.

In Mailand herrscht Aufregung. Die neuste Sommerkollektion eines berühmten Modeschöpfers ist erschienen. Alle sind begeistert.
Laut Umfrage kennen 7 von 10 Personen bereits die neue Kollektion. 2 von 3 Befragten kannten die Frühlingskollektion des bekannten Modeschöpfers. $\small{90\,\%}$ der Befragten kennen wenigstens eine der beiden Kollektionen.

Untersuche, ob die Kollektionen in Bezug auf Bekanntheit stochastisch unabhängig sind.

Statistiken einer Videothek haben gezeigt, dass $\small{60\,\%}$ der Kunden zu diesem Zeitpunkt aktuelle Kinofilme ausleihen (Zeitraum 10 Wochen) und $\small{45\,\%}$ der Kunden sich gerne die „älteren“ Filme (Zeitraum älter als 10 Wochen) ausleihen.
$\small{15\,\%}$ der Kunden leihen sich nur Videospiele aus.

Untersuche, ob das Ausleihen der aktuellen Filme und das Ausleihen der älteren Filme stochastisch unabhängig sind.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Schnittwahrscheinlichkeit bestimmen

Da $A$ und $B$ stochastisch unabhängige Ereignisse sind, lässt sich folgende Formel anwenden:

$P(A\cap B)=0,28$

Vollständige Lösung anzeigen

Stochastische Unabhängigkeit

Wenn man eine Kugel aus der Urne zieht, beträgt die Wahrscheinlichkeit, eine rote Kugel zu ziehen, $\frac{5}{8}$ . Wenn man die Kugel wieder zurücklegt und erneut zieht, beträgt die Wahrscheinlichkeit, eine rote Kugel zu ziehen, wieder $\frac{5}{8}$ . Legt man die Kugel nicht wieder zurück, liegt die Wahrscheinlichkeit, im zweiten Zug wieder eine rote Kugel zu ziehen, nur noch bei $\frac{4}{7}$ .

Beim Ziehen mit Zurücklegen sind die einzelnen Züge stochastisch unabhängig.

Beim Ziehen ohne Zurücklegen sind die einzelnen Züge stochastisch abhängig (das Ergebnis des zweiten Zuges hängt vom Ergebnis des ersten Zuges ab usw.).

Wahrscheinlichkeit bestimmen

Da $A$ und $B$ stochastisch unabhängig sind, gilt $P(A\cap B)=P(A)\cdot P(B)$ .

Aufgelöst nach $P(B)$ ergibt sich:

$P(B)=\dfrac{P(A\cap B)}{P(A)}=\dfrac{0,1}{0,4}=0,25$

Wahrscheinlichkeit bestimmen

$p=P(B)$ sei der Bekanntheitsgrad von Stefan Raab.

Es ergibt sich folgendes Baumdiagramm mit $k=\;$ kennen, $\overline{k}=\;$ nicht kennen, $F=\;$ Frau und $M=\;$ Mann:

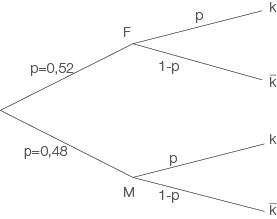Diagramm mit Wahrscheinlichkeiten und Entscheidungsbaum für zwei Ereignisse F und M.

Da $M$ und $B$ stochastisch unabhängig sind, sind auch $M$ und $\overline{B}$ stochastisch unabhängig. Es gilt:

$\begin{array}[t]{rll} P(M\cap\overline{B})=&P(M)\cdot P(\overline{B})\\[5pt] P(\overline{B})=&\dfrac{P(M\cap\overline{B})}{P(M)}\\[5pt] 1-p=&\dfrac{0,16}{0,48} \Rightarrow\;p=\dfrac{2}{3} \end{array}$

Somit beträgt der Bekanntheitsgrad von Stefan Raab in dieser Umfrage $p=\dfrac{2}{3}$ .

Ein kleinerer Frauenanteil in der Umfrage würde einen größeren Männeranteil in der Umfrage bedeuten.

Siehst du dir die Formel $P(\overline{B})=\frac{P(M\cap\overline{B})}{P(M)}$ an, so würde ein größerer Männeranteil bewirken, dass $P(\overline{B})$ kleiner wird und damit $P(B)$ (der Bekanntheitsgrad) größer.

Würde man nur Männer befragen, also $P(M)=1$ , ergibt sich $P(\overline{B})=\frac{0,16}{1}$ und damit $P(B)=1-0,16=0,84\%$ , was eine deutliche Steigerung des Bekanntheitsgrades zur Folge hätte.

Stochastische Unabhängigkeit überprüfen

Sei $S$ das Ereignis „Ein Befragter kennt die Sommerkollektion“ und $F$ das Ereignis „Ein Befragter kennt die Frühjahrskollektion“.

Aus der Aufgabenstellung folgen die Wahrscheinlichkeiten $P(S)=0{,}7$ und $P(F)=\frac{2}{3}$ . Weiterhin ist die Wahrscheinlichkeit 0,9 dafür gegeben, dass ein Befragter wenigstens eine der beiden Kollektionen kennt. Dies entspricht dem Ereignis $F\cup S$ . Daraus folgt direkt: Mit einer Wahrscheinlichkeit von $10\,\%$ kennt ein Befragter keine der beiden Kollektionen, d. h. $P(\overline{F}\cap \overline{S})=0{,}1$ .

Du kannst die Situation gut in einer Vierfeldertafel darstellen. Die fett gedruckten Werte sind die aus der Aufgabenstellung, die übrigen lassen sich über einfaches Addieren und Subtrahieren berechnen:

	$F$	$\overline{F}$
$S$	$\frac{7}{15}$	$\frac{7}{30}$	$\boldsymbol{0{,}7}$
$\overline{S}$	0,2	$\boldsymbol{0{,}1}$	0,3
	$\boldsymbol{\frac{2}{3}}$	$\frac{1}{3}$	1

Untersuche nun die Ereignisse $S$ und $F$ auf stochastische Abhängigkeit:

$P(F\cap S)=\dfrac{7}{15}$ $\qquad$ und $\qquad$ $P(F)\cdot P(S)=\dfrac{2}{3}\cdot0{,}7=\dfrac{7}{15}$

Also ist $P(F\cap S)=P(F)\cdot P(S)$ und die Ereignisse sind stochastisch unabhängig.

Stochastische Unabhängigkeit überprüfen

Sei $N$ das Ereignis „Ein Kunde leiht neuere Kinofilme aus“ und $A$ das Ereignis „Ein Kunde leiht ältere Filme aus“. Aus der Aufgabenstellung folgen die Wahrscheinlichkeiten $P(N)=0{,}6$ und $P(A)=0{,}45$ .

Weiterhin ist gegeben, dass $15\,\%$ der Kunden nur Videospiele ausleihen. Sie leihen also weder aktuelle noch ältere Kinofilme aus. Damit gilt: $P(\overline{N}\cap\overline{A})=0{,}15$ .

In einer Vierfeldertafel sieht diese Situation aus wie folgt:

	$A$	$\overline{A}$
$N$	0,2	0,4	$\boldsymbol{0{,}6}$
$\overline{N}$	0,25	$\boldsymbol{0{,}15}$	0,4
	$\boldsymbol{0{,}45}$	0,55	1

Untersuche nun die Ereignisse $A$ und $N$ auf stochastische Abhängigkeit:

$P(A\cap N)=0{,}2$ $\qquad$ und $\qquad$ $P(A)\cdot P(N)=0{,}45\cdot0{,}6=0{,}27$

Da $P(A\cap N)\neq P(A)\cdot P(N)$ , sind die Ereignisse stochastisch abhängig.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?