Ableitung gegeben: Eigenschaften von Kurven
Mit Hilfe der ersten Ableitung  einer Funktion
einer Funktion  , kannst du Aussagen über die Eigenschaften des Graphen von
, kannst du Aussagen über die Eigenschaften des Graphen von  machen.
Steigung
Die Steigung des Graphen der Funktion
machen.
Steigung
Die Steigung des Graphen der Funktion  im Punkt
im Punkt  entspricht dem Funktionswert der ersten Ableitung im Punkt
entspricht dem Funktionswert der ersten Ableitung im Punkt  .
.
Extremstellen/Sattelpunkte Die Nullstellen der ersten Ableitungen sind Extremstellen/Sattelpunkte des Graphen von .
Wendepunkte
Hat die erste Ableitung eine Extremstelle, so hat die Funktion
.
Wendepunkte
Hat die erste Ableitung eine Extremstelle, so hat die Funktion  an dieser Stelle einen Wendepunkt.
Monotonie
an dieser Stelle einen Wendepunkt.
Monotonie
 entspricht dem Graphen im folgenden Schaubild:
entspricht dem Graphen im folgenden Schaubild:
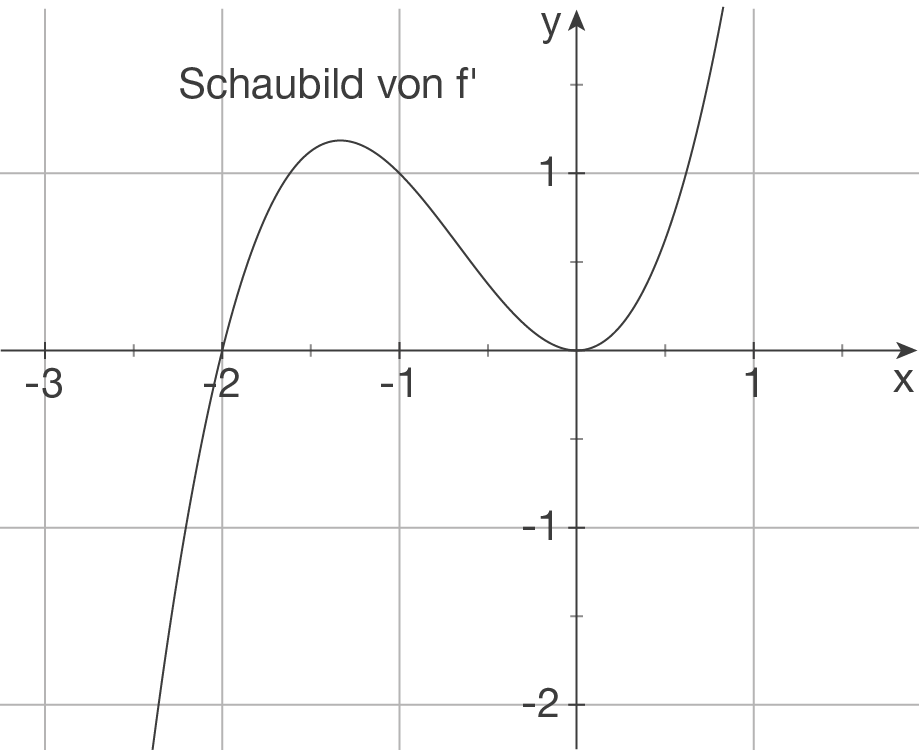
Extremstellen/Sattelpunkte Die Nullstellen der ersten Ableitungen sind Extremstellen/Sattelpunkte des Graphen von
monoton wachsend:
(streng monoton, wenn
)
monoton fallend:
(streng monoton, wenn
).
Beispiel
Die Ableitung von
- Extremstellen/Sattelpunkte:
- Nullstelle bei
der Graph von
hat an der Stelle
einen Tiefpunkt (Vorzeichenwechsel von minus nach plus)
- Doppelte Nullstelle bei
der Graph von
hat einen Sattelpunkt an der Stelle
(kein Vorzeichenwechsel)
- Nullstelle bei
- Wendepunkte:
- Hochpunkt bei
der Graph von
hat an der Stelle
einen Wendepunkt
- Tiefpunkt bei
der Graph von
hat an der Stelle
einen Wendepunkt
- Hochpunkt bei
1.
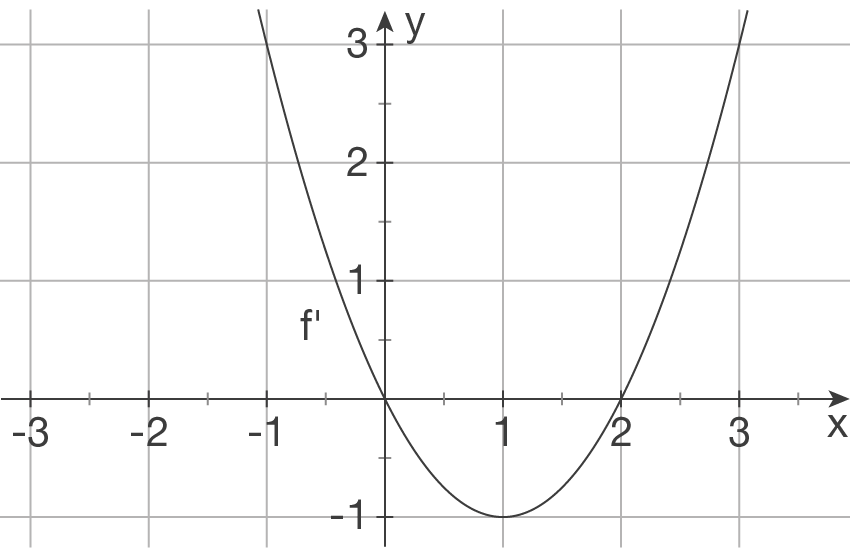
Gegeben ist die Ableitungsfunktion  der Funktion
der Funktion  .
.
Sind die folgenden Aussagen wahr, falsch oder nicht entscheidbar?
Begründe deine Entscheidung.
 ist für
ist für  streng monoton steigend.
streng monoton steigend.
Sind die folgenden Aussagen wahr, falsch oder nicht entscheidbar?
Begründe deine Entscheidung.
a)

(1)
An der Stelle  besitzt
besitzt  einen Tiefpunkt.
einen Tiefpunkt.
(2)
Die Funktion  besitzt mindestens einen Wendepunkt.
besitzt mindestens einen Wendepunkt.
(3)
Für  ist
ist  streng monoton fallend.
streng monoton fallend.
(4)
Die Funktion  weist drei Nullstellen auf.
weist drei Nullstellen auf.
b)

(1)
An der Stelle  besitzt
besitzt  einen Wendepunkt.
einen Wendepunkt.
(2)
(3)
Die Steigung von  an der Stelle
an der Stelle  beträgt
beträgt  .
.
(4)
Bei  besitzt das Schaubild von
besitzt das Schaubild von  eine Tangente, die parallel oder identisch zu
eine Tangente, die parallel oder identisch zu  ist.
ist.
2.
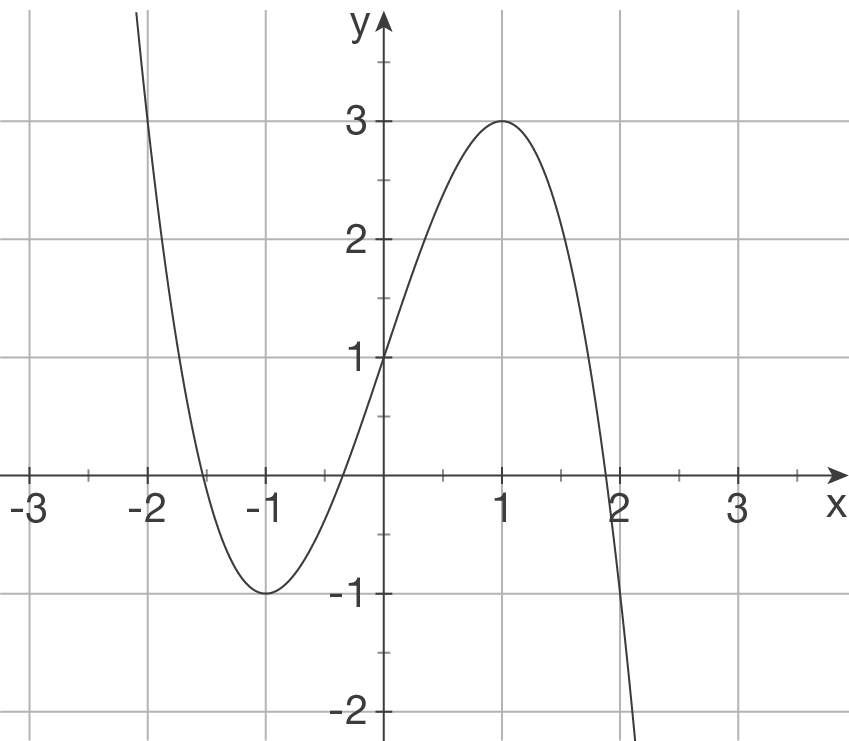
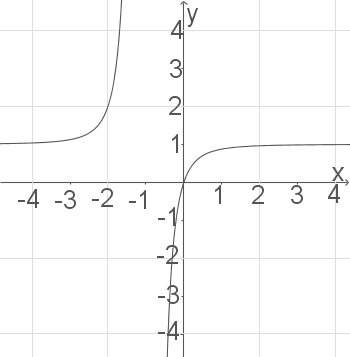
Gegeben ist der Graph der ersten Ableitungsfunktion einer Funktion  .
.
Sind die folgenden Aussagen wahr, falsch oder nicht entscheidbar?
Begründe deine Entscheidung.
 (1)
(1)  besitzt keinen Wendepunkt.
(2) An der Stelle
besitzt keinen Wendepunkt.
(2) An der Stelle  besitzt
besitzt  einen Hochpunkt.
(3) Für
einen Hochpunkt.
(3) Für  ist
ist  monoton steigend.
(4)
monoton steigend.
(4)  besitzt Nullstellen.
besitzt Nullstellen.
 ist für
ist für  streng monoton fallend.
streng monoton fallend.
 besitzt einen Wendepunkt.
besitzt einen Wendepunkt.
 ist symmetrisch zum Punkt
ist symmetrisch zum Punkt  .
.

 ist für
ist für  streng monoton steigend.
streng monoton steigend.
 besitzt einen Wendepunkt.
besitzt einen Wendepunkt.
Sind die folgenden Aussagen wahr, falsch oder nicht entscheidbar?
Begründe deine Entscheidung.
a)

(1)
An der Stelle  besitzt
besitzt  einen Tiefpunkt.
einen Tiefpunkt.
(2)
Die Funktion  besitzt mindestens einen Wendepunkt.
besitzt mindestens einen Wendepunkt.
(3)
Für  ist
ist  ist streng monoton fallend.
ist streng monoton fallend.
(4)
Für  ist
ist  streng monoton fallend.
streng monoton fallend.
(5)
Die Funktion  ist symmetrisch zur y-Achse.
ist symmetrisch zur y-Achse.
b)

c)

(1)
(2)
An der Stelle  besitzt
besitzt  einen Hochpunkt.
einen Hochpunkt.
(3)
Für  ist
ist  streng monoton fallend.
streng monoton fallend.
(4)
(5)
d)

(1)
(2)
An der Stelle  besitzt
besitzt  einen Hochpunkt.
einen Hochpunkt.
(3)
3.
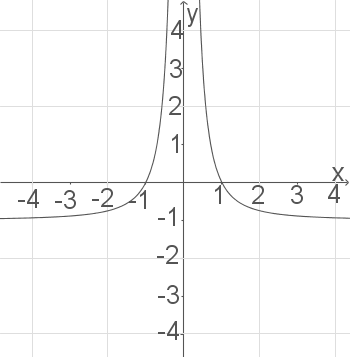
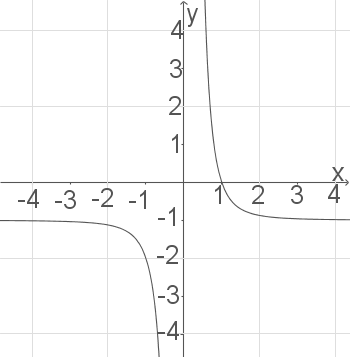
Gegeben ist das Schaubild der Ableitungsfunktion  einer Funktion
einer Funktion  .
.
Entscheide, ob die folgenden Aussagen wahr, falsch oder unentscheidbar sind.
Begründe jeweils deine Antwort.


Entscheide, ob die folgenden Aussagen wahr, falsch oder unentscheidbar sind.
Begründe jeweils deine Antwort.

(1)
Die Funktion  hat an der Stelle
hat an der Stelle  ein lokales Minimum.
ein lokales Minimum.
(2)
Für  ist
ist  streng monoton steigend.
streng monoton steigend.
(3)
Die Funktion  hat mindestens eine Wendestelle.
hat mindestens eine Wendestelle.
(4)
Das Schaubild von  hat mindestens drei Tangenten, die parallel zur Geraden
hat mindestens drei Tangenten, die parallel zur Geraden  sind.
sind.
(5)
4.
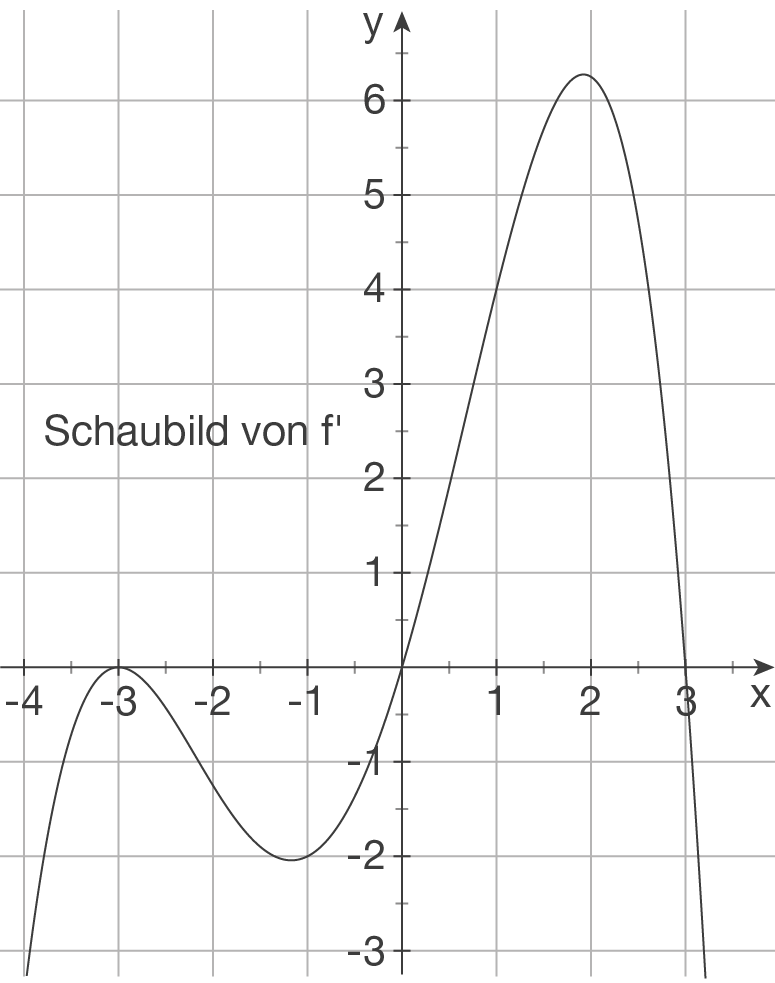
Gegeben ist das Schaubild der Ableitungsfunktion  einer Funktion
einer Funktion  .
.
Entscheide, ob die folgenden Aussagen wahr, falsch oder unentscheidbar sind. Begründe jeweils deine Antwort.
 ist streng monoton wachsend für
ist streng monoton wachsend für  .
.
Entscheide, ob die folgenden Aussagen wahr, falsch oder unentscheidbar sind. Begründe jeweils deine Antwort.

(1)
(2)
Das Schaubild von  hat drei Stellen mit waagrechter Tangente.
hat drei Stellen mit waagrechter Tangente.
(3)
Das Schaubild von  hat mindestens zwei Wendepunkte.
hat mindestens zwei Wendepunkte.
(4)
Es gilt  für alle
für alle ![\( x\in\left[0;3\right]\)](https://www.schullv.de/resources/formulas/bba629283cfa652fb661b11cb0565190b7735cadd23b04d0081f5aec180dfbed_light.svg) .
.
(5)
Das Schaubild von  besitzt bei
besitzt bei  einen Sattelpunkt.
einen Sattelpunkt.
5.
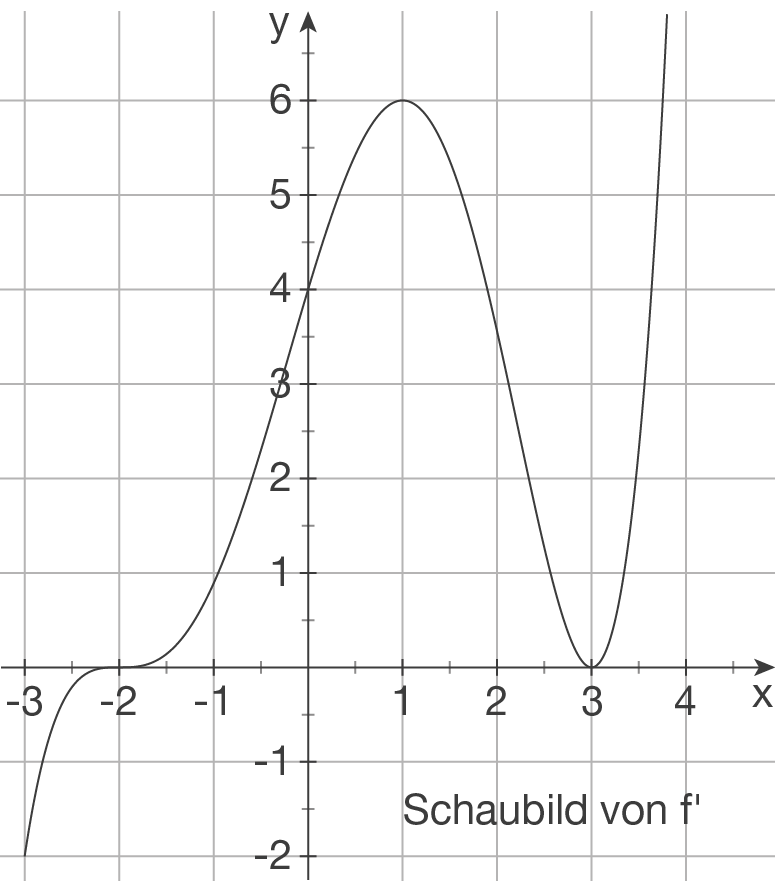
Gegeben ist das Schaubild der Ableitungsfunktion  einer Funktion
einer Funktion  .
.
Entscheide, ob die folgenden Aussagen wahr, falsch oder unentscheidbar sind.
Begründe jeweils deine Antwort.

Entscheide, ob die folgenden Aussagen wahr, falsch oder unentscheidbar sind.
Begründe jeweils deine Antwort.

(1)
Das Schaubild von  hat bei
hat bei  einen Tiefpunkt.
einen Tiefpunkt.
(2)
Das Schaubild von  hat für
hat für  genau zwei Wendepunkte.
genau zwei Wendepunkte.
(3)
Das Schaubild von  verläuft im Schnittpunkt mit der
verläuft im Schnittpunkt mit der  -Achse steiler als die Gerade
-Achse steiler als die Gerade  .
.
(4)
Das Schaubild von  hat einen Hochpunkt an der Stelle
hat einen Hochpunkt an der Stelle  .
.
(5)
6.
Gegeben ist die Ableitungsfunktion der Funktion  .
.
Sind folgende Aussagen wahr, falsch oder nicht entscheidbar?
Begründe deine Entscheidung.
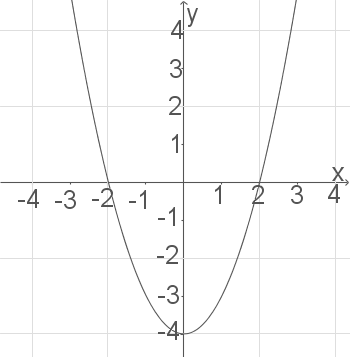
 besitzt einen Wendepunkt.
besitzt einen Wendepunkt.
 besitzt Nullstellen.
besitzt Nullstellen.
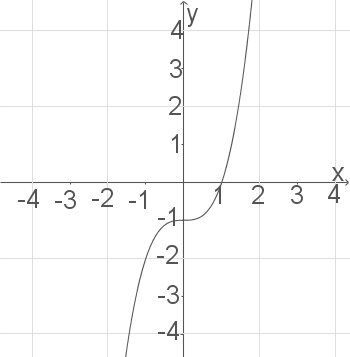
 besitzt einen Wendepunkt.
besitzt einen Wendepunkt.
Sind folgende Aussagen wahr, falsch oder nicht entscheidbar?
Begründe deine Entscheidung.
a)

(1)
(2)
An der Stelle  besitzt
besitzt  einen Tiefpunkt.
einen Tiefpunkt.
(3)
Für  ist
ist  streng monoton fallend.
streng monoton fallend.
(4)
(5)
An der Stelle  besitzt
besitzt  einen Hochpunkt.
einen Hochpunkt.
b)

(1)
(2)
Für  besitzt
besitzt  keine Nullstelle.
keine Nullstelle.
(3)
Für  ist
ist  streng monoton steigend.
streng monoton steigend.
(4)
An der Stelle  liegt ein Tiefpunkt vor.
liegt ein Tiefpunkt vor.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
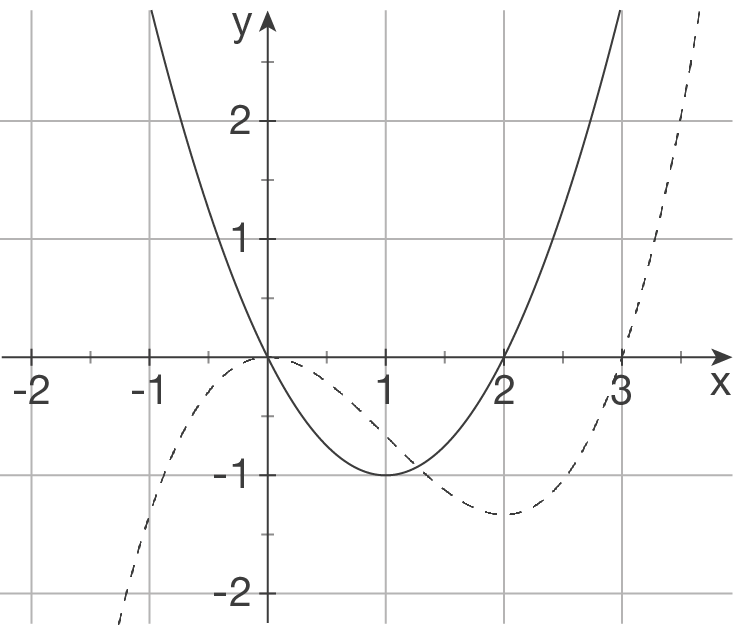
(1)
Falsche Aussage
Die Ableitungsfunktion hat an dieser Stelle einen Tiefpunkt, die Funktion weist demnach einen Wendepunkt an dieser Stelle vor.
weist demnach einen Wendepunkt an dieser Stelle vor.
Die Ableitungsfunktion hat an dieser Stelle einen Tiefpunkt, die Funktion
(2)
Richtige Aussage
Weist an einer Stelle einen Extrempunkt vor, so liegt an dieser Stelle bei
an einer Stelle einen Extrempunkt vor, so liegt an dieser Stelle bei  ein Wendepunkt vor.
ein Wendepunkt vor.
Weist
(3)
Falsche Aussage
Für (mindestens) ist die Funktion streng monoton fallend. Für
(mindestens) ist die Funktion streng monoton fallend. Für  jedoch streng monoton steigend, da der Graph von
jedoch streng monoton steigend, da der Graph von  in diesem Bereich auch oberhalb der
in diesem Bereich auch oberhalb der  -Achse verläuft.
-Achse verläuft.
Für
(4)
Nicht entscheidbare Aussage
Da eine Funktion zweiten Grades ist, ist
eine Funktion zweiten Grades ist, ist  eine Funktion dritten Grades der Form
eine Funktion dritten Grades der Form  . Diese kann drei Nullstellen aufweisen, was jedoch abhängig ist vom absoluten Glied
. Diese kann drei Nullstellen aufweisen, was jedoch abhängig ist vom absoluten Glied  (Verschiebung in positive oder negative
(Verschiebung in positive oder negative  -Richtung).
-Richtung).
Da
b)
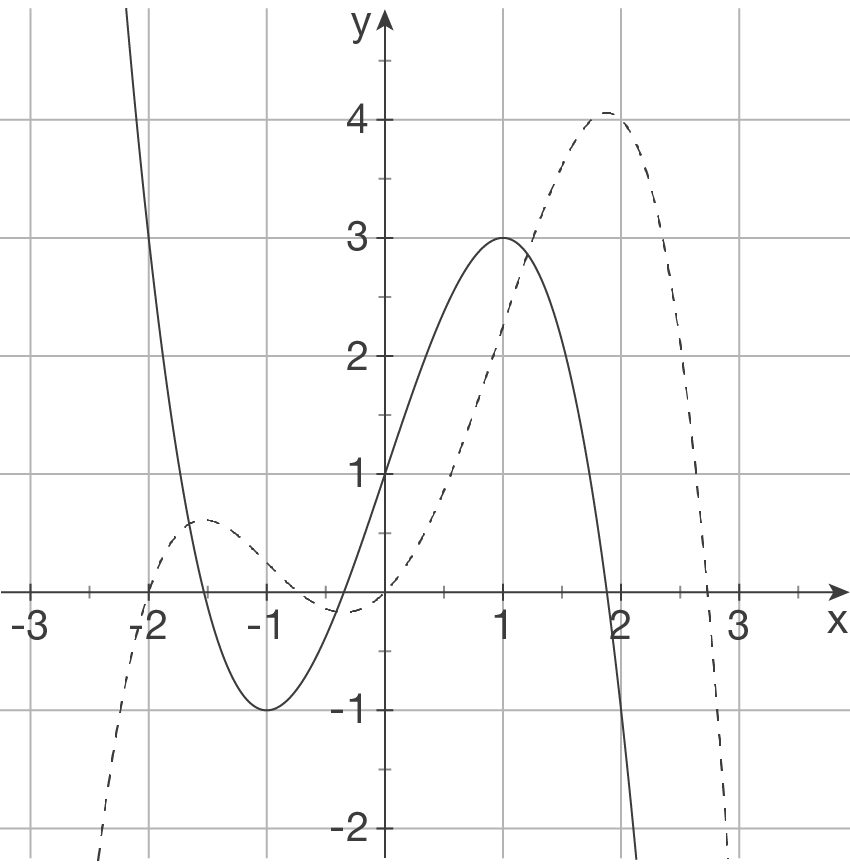
(1)
Richtige Aussage
Da das Schaubild von an dieser Stelle einen Hochpunkt aufweist, besitzt
an dieser Stelle einen Hochpunkt aufweist, besitzt  an diese Stelle einen Wendepunkt. (Wendepunkte sind Punkte mit extremaler Steigung)
an diese Stelle einen Wendepunkt. (Wendepunkte sind Punkte mit extremaler Steigung)
Da das Schaubild von
(2)
Falsche Aussage
Das Schaubild von verläuft bis
verläuft bis  oberhalb der
oberhalb der  -Achse und nur in diesem Bereich liegt für
-Achse und nur in diesem Bereich liegt für  eine positive Steigung vor (und damit ist
eine positive Steigung vor (und damit ist  nur in diesem Bereich monoton steigend). Für
nur in diesem Bereich monoton steigend). Für  gilt jedoch
gilt jedoch  und damit ist der Graph von
und damit ist der Graph von  monoton fallend in diesem Bereich.
monoton fallend in diesem Bereich.
Das Schaubild von
(3)
Richtige Aussage
 gibt die Steigung von
gibt die Steigung von  an (
an ( gibt die Steigung der Tangenten an den Graphen von
gibt die Steigung der Tangenten an den Graphen von  an jeder beliebigen Stelle
an jeder beliebigen Stelle  an). An der Stelle
an). An der Stelle  hat
hat  den
den  -Wert
-Wert  . Damit beträgt die Steigung der Tangente an den Graphen von
. Damit beträgt die Steigung der Tangente an den Graphen von  an der Stelle
an der Stelle  gleich 1.
gleich 1.
(4)
Richtige Aussage
Die Steigung an der Stelle ist für
ist für  gleich Null. Die Steigung der Geraden
gleich Null. Die Steigung der Geraden  ist ebenfalls
ist ebenfalls  . Demnach sind Tangente und Gerade parallel oder identisch.
. Demnach sind Tangente und Gerade parallel oder identisch.
Die Steigung an der Stelle
2.
a)

(1)
Falsch, da für  eine pos. Steigung und für
eine pos. Steigung und für  eine neg. Steigung vorliegt (VZW von
eine neg. Steigung vorliegt (VZW von  nach
nach  ). Es handelt sich also um einen Hochpunkt.
). Es handelt sich also um einen Hochpunkt.
(2)
Falsch bzw. nicht entscheidbar, der Graph von  besitzt keine Extrempunkte, also sind die notwendige und hinreichende Bedingung für ein Extremum von
besitzt keine Extrempunkte, also sind die notwendige und hinreichende Bedingung für ein Extremum von  nicht erfüllt, diese sind aber auch genau die Bedingungen für eine Wendestelle von
nicht erfüllt, diese sind aber auch genau die Bedingungen für eine Wendestelle von  . Somit ist nicht gewährleistet, dass der Graph von
. Somit ist nicht gewährleistet, dass der Graph von  einen Wendepunkt besitzt.
einen Wendepunkt besitzt.
(3)
Richtig, es liegt in diesem Intervall an jeder Stelle eine negative Steigung vor, da der Graph von  im kompletten Bereich unterhalb der
im kompletten Bereich unterhalb der  -Achse verläuft.
-Achse verläuft.
(4)
Falsch für  liegt eine positive Steigung vor. Erst ab
liegt eine positive Steigung vor. Erst ab  ist der Graph von
ist der Graph von  streng monoton fallend.
streng monoton fallend.
(5)
Falsch, zwischen  und
und  bzw.
bzw.  und
und  liegt immer eine positive Steigung vor, das bedeutet, dass keine Symmetrie zur
liegt immer eine positive Steigung vor, das bedeutet, dass keine Symmetrie zur  -Achse vorliegen kann.
-Achse vorliegen kann.
b)

(1)
Richtig, die Ableitungsfunktion hat keinen Extrempunkt, also kann kein Wendepunkt bei  vorliegen.
vorliegen.
(2)
Falsch, da  eine neg. Steigung und für
eine neg. Steigung und für  eine pos. Steigung vorliegt (VZW von
eine pos. Steigung vorliegt (VZW von  nach
nach  ). Es handelt sich also um einen Tiefpunkt.
). Es handelt sich also um einen Tiefpunkt.
(3)
Richtig, denn in diesem Intervall verläuft der Graph von  oberhalb der
oberhalb der  -Achse.
-Achse.
(4)
Unentscheidbar, denn die Ableitungsfunktion gibt nicht die Lage der Funktion an, lediglich die Steigung.
c)

(1)
Richtig, denn für diesen Bereich weist  immer eine negative Steigung auf.
immer eine negative Steigung auf.
(2)
Richtig, für  liegt bei
liegt bei  eine positive Steigung, für
eine positive Steigung, für  eine negative Steigung vor (VZW von
eine negative Steigung vor (VZW von  nach
nach  ).
).
(3)
Falsch, bei  ändert sich die Steigung von positiv nach negativ.
ändert sich die Steigung von positiv nach negativ.
(4)
Falsch, der Graph von  besitzt keinen Extrempunkt, also besitzt der Graph von
besitzt keinen Extrempunkt, also besitzt der Graph von  keinen Wendepunkt.
keinen Wendepunkt.
(5)
Falsch, denn  gibt keine Aussage über die Lage von
gibt keine Aussage über die Lage von  und da bei
und da bei  ein Vorzeichenwechsel stattfindet und für
ein Vorzeichenwechsel stattfindet und für  der Graph von
der Graph von  streng monoton fällt, kann keine Symmetrie zu
streng monoton fällt, kann keine Symmetrie zu  vorliegen.
vorliegen.
d)

(1)
Richtig, da in diesem Intervall die Steigung von  immer positiv (
immer positiv ( ) ist.
) ist.
(2)
Falsch, für  liegt eine negative, für
liegt eine negative, für  eine positive Steigung vor (VZW von
eine positive Steigung vor (VZW von  nach
nach  ).
).  hat damit an der Stelle
hat damit an der Stelle  einen Tiefpunkt.
einen Tiefpunkt.
(3)
Richtig, bei  hat
hat  eine Wendestelle, da der Graph von
eine Wendestelle, da der Graph von  an dieser Stelle einen Tiefpunkt hat.
an dieser Stelle einen Tiefpunkt hat.
3.
(1)
Falsch. An der Stelle  liegt zwar eine Nullstelle von
liegt zwar eine Nullstelle von  und damit eine potentielle Extremstelle von
und damit eine potentielle Extremstelle von  , allerdings handelt es sich bei
, allerdings handelt es sich bei  um einen Sattelpunkt, denn der Graph der Funktion bleibt für
um einen Sattelpunkt, denn der Graph der Funktion bleibt für  und
und  im positiven Bereich, es findet also kein Vorzeichenwechsel statt.
im positiven Bereich, es findet also kein Vorzeichenwechsel statt.
(2)
Falsch. Für  ist der Graph von
ist der Graph von  nur monoton steigend, da bei
nur monoton steigend, da bei  die Steigung gleich Null ist.
die Steigung gleich Null ist.
(3)
Richtig. Wendestellen sind Punkte mit extremaler Steigung. Da  zwei Extremstellen besitzt, besitzt
zwei Extremstellen besitzt, besitzt  zwei Wendestellen.
zwei Wendestellen.
(4)
Richtig. Drei Tangenten, die parallel zur Geraden  sind bedeutet, dass der Graph von
sind bedeutet, dass der Graph von  drei Tangenten besitzt, die eine Steigung von
drei Tangenten besitzt, die eine Steigung von  haben.
haben.
Schaut man sich das Schaubild von an und so stellt man fest, dass es drei Punkte gibt, die die
an und so stellt man fest, dass es drei Punkte gibt, die die  -Koordinate
-Koordinate  besitzen. Die Tangenten an den Graphen von
besitzen. Die Tangenten an den Graphen von  an die Stellen (
an die Stellen ( -Koordinaten) dieser Punkte haben damit die Steigung
-Koordinaten) dieser Punkte haben damit die Steigung  .
.
Schaut man sich das Schaubild von
(5)
Falsch. Für  ist
ist  monoton steigend (
monoton steigend ( -Werte von
-Werte von  sind im positiven Bereich). Damit gilt umgekehrt
sind im positiven Bereich). Damit gilt umgekehrt  .
.
4.
(1)
Falsch. Für  sind die
sind die  -Werte des Graphen von
-Werte des Graphen von  negativ, d.h. er verläuft unterhalb der
negativ, d.h. er verläuft unterhalb der  -Achse. Somit ist der Graph von
-Achse. Somit ist der Graph von  für
für  monoton fallend. Für
monoton fallend. Für  sind die
sind die  -Werte des Graphen von
-Werte des Graphen von  positiv. Somit ist der Graph von
positiv. Somit ist der Graph von  für
für  monoton steigend.
monoton steigend.
(2)
Richtig.  hat drei Nullstellen und damit drei Stellen mit der Steigung
hat drei Nullstellen und damit drei Stellen mit der Steigung  . Die bedeutet drei waagrechte Tangenten.
. Die bedeutet drei waagrechte Tangenten.
(3)
Richtig. Da der Graph von  drei Extrempunkte besitzt und Wendestellen Punkte mit extremer Steigung sind, besitzt
drei Extrempunkte besitzt und Wendestellen Punkte mit extremer Steigung sind, besitzt  mindestens zwei Wendestellen.
mindestens zwei Wendestellen.
(4)
Unentscheidbar. Der Graph von  ist zwar für
ist zwar für ![\(x\in\left[0;3\right]\)](https://www.schullv.de/resources/formulas/36884a1b7cccbea70a1eb61d018cede03b0bb73633ac30020267d3e97436c16f_light.svg) monoton steigend, allerdings sagt diese Information nichts über die tatsächliche Lage des Graphen von
monoton steigend, allerdings sagt diese Information nichts über die tatsächliche Lage des Graphen von  aus. Man kann daher keine Aussage treffen, ob
aus. Man kann daher keine Aussage treffen, ob  in diesem Intervall größer als
in diesem Intervall größer als  ist.
ist.
(5)
Richtig. Bei  berührt der Graph von
berührt der Graph von  die
die  -Achse. Es findet kein Vorzeichenwechsel statt. Die Steigung von
-Achse. Es findet kein Vorzeichenwechsel statt. Die Steigung von  bleibt negativ. Es handelt sich somit um einen Sattelpunkt.
bleibt negativ. Es handelt sich somit um einen Sattelpunkt.
5.
(1)
Falsch. Bei  berührt der Graph von
berührt der Graph von  die
die  -Achse. Es findet bei
-Achse. Es findet bei  kein Vorzeichenwechsel statt. Es handelt sich also um einen Stattelpunkt.
kein Vorzeichenwechsel statt. Es handelt sich also um einen Stattelpunkt.
(2)
Richtig. Für  besitzt
besitzt  genau zwei Extremstellen. Wendestellen sind Punkte mit extremer Steigung.
genau zwei Extremstellen. Wendestellen sind Punkte mit extremer Steigung.
(3)
Richtig. Schaut man sich den  -Wert des Graphen von
-Wert des Graphen von  an der Stelle
an der Stelle  (Ursprung) an, so liest man aus dem Schaubild
(Ursprung) an, so liest man aus dem Schaubild  ab. Dies bedeutet, dass die Tangente an
ab. Dies bedeutet, dass die Tangente an  an der Stelle
an der Stelle  die Steigung
die Steigung  hat. Somit ist die Tangente dort steiler als die Gerade
hat. Somit ist die Tangente dort steiler als die Gerade  .
.
(4)
Falsch. An der Stelle  findet ein Vorzeichenwechsel von
findet ein Vorzeichenwechsel von  nach
nach  statt. Somit liegt an der Stelle ein Tiefpunkt vor.
statt. Somit liegt an der Stelle ein Tiefpunkt vor.
(5)
Richtig. Für  steigt der Graph von
steigt der Graph von  monoton (
monoton ( -Werte von
-Werte von  sind positiv). Somit ist
sind positiv). Somit ist  .
.
6.
a)

(1)
Richtig, der Graph von  besitzt an der Stelle
besitzt an der Stelle  einen Wendepunkt, da der Graph von
einen Wendepunkt, da der Graph von  einen Extrempunkt an dieser Stelle aufweist.
einen Extrempunkt an dieser Stelle aufweist.
(2)
Falsch, da an der Stelle  bei dem Graphen von
bei dem Graphen von  ein Tiefpunkt vorliegt, liegt beim Graphen von
ein Tiefpunkt vorliegt, liegt beim Graphen von  an dieser Stelle ein Wendepunkt vor.
an dieser Stelle ein Wendepunkt vor.
(3)
Richtig, in diesem Bereich liegt bei  an jeder Stelle eine negative Steigung vor.
an jeder Stelle eine negative Steigung vor.
(4)
Richtig, da  eine Funktion 2. Grades ist, ist
eine Funktion 2. Grades ist, ist  eine Funktion 3. Grades. Diese besitzt mindestens eine Nullstelle.
eine Funktion 3. Grades. Diese besitzt mindestens eine Nullstelle.
(5)
Richtig, für  liegt eine positive, für
liegt eine positive, für  eine negative Steigung vor (VZW von
eine negative Steigung vor (VZW von  nach
nach  ).
).
b)

(1)
Falsch, der Graph von  besitzt keinen Extrempunkt, also besitzt der Graph von
besitzt keinen Extrempunkt, also besitzt der Graph von  keinen Wendepunkt.
keinen Wendepunkt.
(2)
Unentscheidbar,  lediglich die Steigung von
lediglich die Steigung von  an, nicht aber die Lage des Graphen von
an, nicht aber die Lage des Graphen von  an.
an.
(3)
Falsch, der Graph von  wäre streng monoton fallend, da immer eine negative Steigung in diesem Intervall vorliegt.
wäre streng monoton fallend, da immer eine negative Steigung in diesem Intervall vorliegt.
(4)
Richtig, für  liegt eine negative, für
liegt eine negative, für  eine positive Steigung vor (VZW von
eine positive Steigung vor (VZW von  nach
nach  ).
).