Exponentialfunktionen

Du kannst eine Exponentialfunktion auf folgende Eigenschaften überprüfen:

Eigenschaft	Methode
Schnittpunkte mit den Koordinatenachsen $(x_0\mid y_0)$	x-Achse: Nullstelle bestimmen, d.h. $y_0 = 0$ , setze also $f(x_0)=0$ und löse nach $x_0$ auf y-Achse: Funktionswert an der Stelle $x_0 = 0$ berechnen, also $y_0 = f(0)$
Verhalten im Unendlichen	$\lim\limits_{x\to\infty}\quad$ bzw. $\quad \lim\limits_{x\to\,-\infty}$
Extrempunkt $(x_E\mid y_E)$	Notwendiges Kriterium: $f‘(x_E)=0$ Hinreichendes Kriterium: Hochpunkt: $f‘‘(x_E) \lt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $+$ nach $-$ Tiefpunkt: $f‘‘(x_E) \gt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $-$ nach $+$
Wendepunkt $(x_W\mid y_W)$	Notwendiges Kriterium: $f‘‘(x_W)=0$ Hinreichendes Kriterium: $f‘‘‘(x_W) \neq 0$ oder Vorzeichenwechsel von $f‘‘(x)$ in $x_W$
Graph skizzieren	Verwende zum Skizzieren markante Stellen z.B. Nullstellen, Hochpunkte, usw.
Symmetrie	achsensymmetrisch: $f(x)=f(-x)$ punktsymmetrisch: $-f(x)=f(-x)$

Gegeben ist die Funktion $f$ mit $f\left(x\right)=\mathrm e^{x+1}+x$ . Ihr Schaubild sei $K_f$ .

Weise nach, dass $f$ an der Stelle $x=-1$ eine Nullstelle hat und bestimme den Schnittpunkt von $K_f$ mit der $y$ -Achse.

Wie ist es zu erklären, dass sich die $y$ -Werte im Bereich von $x\lt 0$ mehr und mehr den $x$ -Werten annähern?
Beispiel:

$x$	$y$
$-2,5$	$-2,277$
$-4,5$	$-4,47$
$-6,5$	$-6,496$

Skizziere anhand der bisherigen Ergebnisse den Verlauf von $K_f$ in einem Koordinatensystem.

Weise nach, dass $f$ nur an einer Stelle die Steigung $2$ besitzt.

Angenommen, du sollst das Schaubild der Funktion $g$ mit $g\left(x\right)=\mathrm e^{-x}+1$ ohne Wertetabelle und nur mit Hilfe des Schaubildes der $\mathrm e$ -Funktion skizzieren, wie würdest du vorgehen (verschieben, spiegeln, ...)?

Gegeben ist die Funktion $f_k$ mit $f_l\left(x\right)=\mathrm e^{2x^2}+k$ . Ihr Schaubild sei $K_f$ .

Bestimme die Anzahl der Schnittpunkte von $K_f$ mit der $x$ -Achse in Abhängigkeit von $k$ .

Bestimme die Extrema von $K_f$ . Wie wirkt sich das $k$ im Schaubild aus?

Skizziere anhand der bisherigen Ergebnisse den Verlauf von $K_f$ für $k=-2$ in einem Koordinatensystem.

Beweise, dass $K_f$ zur $y$ -Achse symmetrisch ist.

Angenommen, du willst das Schaubild dieser Funktion um $a$ Einheiten nach rechts verschieben, wie gehst du vor?

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$f\left(x\right)=\mathrm e^{x+1}+x$

$\boldsymbol{f\left(-1\right)}$ berechnen

$\begin{array}{rllll} f\left(-1\right)&=\mathrm e^{-1+1}+\left(-1\right)\\[3pt] &=\mathrm e^0-1\\[3pt] &=1-1\\[3pt] f\left(-1\right)=0 \end{array}$

$f$ besitzt an der Stelle $x=-1$ eine Nullstelle.

Schnittpunkte mit der $\boldsymbol{y}$ -Achse bestimmen: $\boldsymbol{x=0}$ setzen und ausrechnen

$\begin{array}{rllll} f\left(0\right)&=\mathrm e^{0+1}+0\\[3pt] &=\mathrm e \end{array}$

Daraus ergibt sich der Punkt $P\left(0\middle|\mathrm e\right)$ .

Grenzwert für $\boldsymbol{x\to-\infty}$ betrachten

$\lim\limits_{x\to-\infty}{\mathrm e^{x+1}+x}$

$\mathrm e^{x+1}$ läuft für $x\to-\infty$ gegen 0:

$\mathrm e^{-z}=\dfrac{1}{\mathrm e^{z}}\to0$ für $z\to\infty$ .

So bleibt nur noch $\lim\limits_{x\to-\infty}f\left(x\right)=x$ , d.h. für $x\to-\infty$ nähert sich das Schaubild von $f$ der Geraden $y=x$ an. Diese Gerade hat die Eigenschaft, dass die $x$ - und $y$ -Koordinaten all ihrer Punkte gleich sind.

Skizze zeichnen

Graf einer mathematischen Funktion mit einer Kurve im Koordinatensystem.

Nachweisen, dass $\boldsymbol{f}$ nur an einer Stelle die Steigung $\boldsymbol{2}$ besitzt

Die Steigung von $f$ wird dir durch die erste Ableitung $f‘$ gegeben. Zeige also, dass $f‘$ nur an einer Stelle den Wert $2$ annimmt. Bestimme zunächst eine Gleichung von $f‘$ nach der Kettenregel.

$\begin{array}{rlll} f\left(x\right)&=\mathrm e^{x+1}+x\\[3pt] f‘\left(x\right)&=\mathrm e^{x+1}+1 \end{array}$

$f‘\left(x\right)=2$ setzen und
nach $x$ auflösen:

$\begin{array}{rllll} \mathrm e^{x+1}+1&=2&\scriptsize{\mid\;-1}\\[3pt] \mathrm e^{x+1}&=1&\scriptsize{\mid\;\ln{\left(\;\right)}}\\[3pt] \ln{\left(\mathrm e^{x+1}\right)}&=\ln{\left(1\right)}\\[3pt] x+1&=0&\scriptsize{\mid\;-1}\\[3pt] x&=-1 \end{array}$

Vorgehen bei Skizzieren des Funktionsgraphen ohne Wertetabelle schildern

Das Schaubild der gegebenen Funktion geht aus dem Schaubild der $\mathrm e$ -Funktion durch Verschiebung und Spiegelung hervor.

Der Exponent $-x$ drückt aus, dass das Schaubild der $\mathrm e$ -Funktion an der $y$ -Achse gespiegelt wird, der Summand $1$ , dass es um 1 LE in positive $y$ -Richtung („nach oben“) verschoben wird.

So lässt sich das Schaubild dieser Funktion schnell mit Hilfe des Schaubildes der $\mathrm e$ -Funktion zeichnen.

$f\left(x\right)=\mathrm e^{2x^2}+k$

Schnittpunkte mit der $\boldsymbol{x}$ -Achse bestimmen: $\boldsymbol{f\left(x\right)=0}$ setzen und nach $\boldsymbol{x}$ auflösen

$\begin{array}{rllll} \mathrm e^{2x^2}+k&=0&\scriptsize{\mid\;-k}\\[5pt] \mathrm e^{2x^2}&=-k&\scriptsize{\mid\;\ln{\left(\;\right)}}\\[5pt] \ln{\left(\mathrm e^{2x^2}\right)}&=\ln{\left(-k\right)}\\[5pt] 2x^2&=\ln{\left(-k\right)}&\scriptsize{\mid\;:2}\\[5pt] x^2&=\dfrac{1}{2}\ln{\left(-k\right)}&\scriptsize{\mid\;\sqrt{\;}}\\[5pt] x_{1,2}&=\pm\sqrt{\dfrac{1}{2}\ln{\left(-k\right)}} \end{array}$

Es fällt auf, dass es von $k$ abhängt, ob $f$ Nullstellen besitzt oder nicht.
Für $k\geq0$ gibt es keine Nullstellen, weil es nicht möglich ist, den Logarithmus einer negativen Zahl oder von $0$ zu berechnen.

Aufgrund des Definitionsbereichs der $\ln$ -Funktion, muss also $k<0$ sein.

Betrachte nun aber die Wurzel: $\ln(x)$ ist negativ für $0\lt x\lt 1$ . Aus einer negativen Zahl kann aber keine Wurzel gezogen werden. Deshalb fallen auch die Werte $-1\lt k\lt 0$ weg.

Es bleibt $k\leq-1$ :

Für $k=-1$ gibt es genau eine Nullstelle, nämlich $x=0$ . Der Logarithmus von 1 ist immer 0.

Für $k\lt -1$ gibt es genau zwei Nullstellen.

Extrema bestimmen

Ableitungen bilden

$\begin{array}{rlll} f\left(x\right)&=\mathrm e^{2x^2}+k\\[5pt] f‘\left(x\right)&=4x\mathrm e^{2x^2}\\[5pt] f‘‘\left(x\right)&=4\mathrm e^{2x^2}+4x\cdot4x\mathrm e^{2x^2}\\[5pt] &=4\mathrm e^{2x^2}+16x^2\mathrm e^{2x^2}\\[5pt] &=\mathrm e^{2x^2}\cdot\left(4+16x^2\right) \end{array}$

$f‘\left(x\right)=0$ setzen

$\begin{array}{rllll} 4x\mathrm e^{2x^2}&=0&\scriptsize{\mid\;:4}\\[5pt] x\mathrm e^{2x^2}&=0 \end{array}$

Ein Produkt ist 0, wenn einer der Faktoren 0 ist:

$\begin{array}{rllrllrll} x_1&=0\\ \mathrm e^{2x^2}&=0 \end{array}$

Diese Gleichung hat keine Lösung, da man $\mathrm e$ mit keiner Zahl potenzieren kann, damit es 0 wird.
$f$ hat also nur eine Extremstelle bei $x=0$ .

Hinreichende Bedingung überprüfen

$\begin{array}{rllll} f‘‘\left(0\right)&=\mathrm e^{0}\cdot\left(4+16\cdot0\right)\\[5pt] &=1\cdot4 \; \scriptsize{>0: \text{Minimum}} \end{array}$

Das $k$ verschiebt das Schaubild nach oben und nach unten, es verändert also die Lage des Schaubilds.

Skizze zeichnen

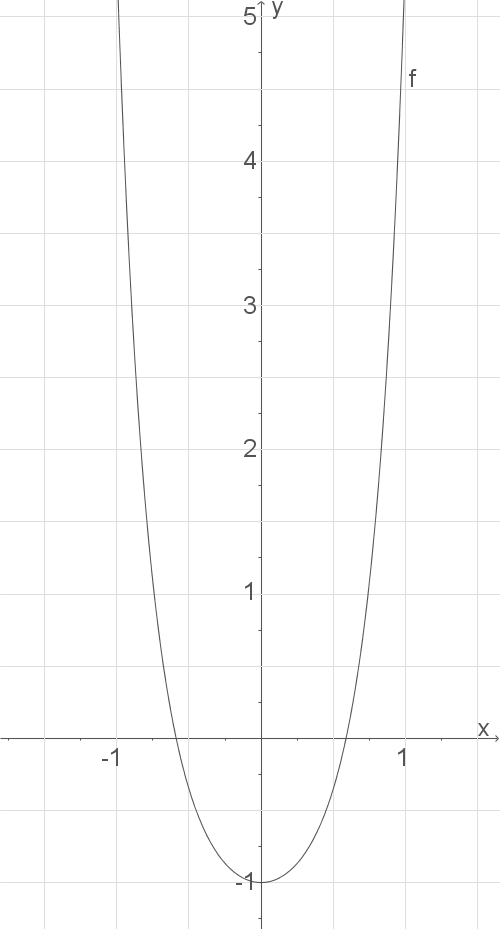
Graf einer Parabel mit Achsen und Gitterlinien.

Achsensymmetrie nachweisen

Behauptung:

$K_f$ ist achsensymmetrisch zu $x=0$

Zu zeigen:

$f\left(x\right)=f\left(-x\right)$

Beweis:

$\begin{array}{rll} \mathrm e^{2x^2}+k&=\mathrm e^{2\left(-x\right)^2}+k\\[5pt] \mathrm e^{2x^2}+k&=\mathrm e^{2x^2}+k \end{array}$

Dies ist eine wahre Aussage.
Die Achsensymmetrie zu $x=0$ ist also bewiesen.

Verschieben des Funktionsgraphen um $\boldsymbol{a}$ Einheiten

Um die Funktion um $a$ Einheiten in positive $x$ -Richtung zu verschieben, muss man direkt beim $x$ eingreifen. Dies lässt sich leicht am Beispiel der Normalparabel verdeutlichen:

$y=x^2\\ \scriptsize{\text{Schaubild verläuft durch den Ursprung}}\\[5pt] y=\left(x+1\right)^2\\\scriptsize{\text{Schaubild verläuft durch} P\left(-1\middle|0\right)\\\text{Verschiebung um 1 LE in neg. x-Richtung}}\\[5pt] y=\left(x-1\right)^2\\\scriptsize{\text{Schaubild verläuft durch} P\left(1\middle|0\right)\\\text{Verschiebung um 1 LE in pos. x-Richtung}}$

Um das Schaubild der Funktion $f$ also um $a$ Einheiten in positive $x$ -Richtung zu verschieben, muss die Funktionsgleichung lauten wie folgt:

$f\left(x\right)=\mathrm e^{2\left(x-a\right)^2}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?