Gebrochenrationale Funktionen

Du kannst eine gebrochenrationale Funktion $f(x)=\dfrac{Z}{N}= \dfrac{a_1x^n + a_2x^{n-1}+ a_3x^{n-2}+... }{b_1x^m+b_2 x^{m-1}+b_3x^{m-2}+...}$ auf folgende Eigenschaften überprüfen:

Eigenschaft	Methode
Definitionsmenge	Definitionslücken berechnest du, indem du den Nenner gleich Null setzt und nach $x$ auflöst. $N(x)=0$
Schnittpunkte mit den Koordinatenachsen $(x_0\mid y_0)$	x-Achse: Nullstelle bestimmen, d.h. $y_0 = 0$ , setze also $f(x_0)=0$ und löse nach $x_0$ auf y-Achse: Funktionswert an der Stelle $x_0 = 0$ berechnen, also $y_0 = f(0)$
Verhalten im Unendlichen	$\lim\limits_{x\to\infty}$ bzw. $\lim\limits_{x\to\,-\infty}$
Asymptoten	senkrechte Asymptote: Definitionslücke, setze also den Nenner mit Null gleich Betrachte den höchsten Nenner- und Zählergrad der Funktion. $f(x)=\dfrac{ax^n + ... }{bx^m+...}$ waagerechte Asymptote: $n \lt m$ : x-Achse ist waagrechte Asymptote $n=m$ : $\lim\limits_{x\to\infty} f(x)$ ist waagrechte Asymptote schiefe Asymptote für $n= m+1$ : Ist der Grad des Zählers um 1 größer als der des Nenners, führe eine Polynomdivision durch. Das Ergebnis ist dann die Gleichung einer schiefen Asymptote.
Monotonieverhalten	streng monoton steigend, wenn $\(f$ streng monoton fallend, wenn $\(f$
Extrempunkt $(x_E\mid y_E)$	Notwendiges Kriterium: $\(f$ Hinreichendes Kriterium: Hochpunkt: $f‘‘(x_E) \lt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $+$ nach $-$ Tiefpunkt: $f‘‘(x_E) \gt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $-$ nach $+$
Wendepunkt $(x_W\mid y_W)$	Notwendiges Kriterium: $f‘‘(x_W)=0$ Hinreichendes Kriterium: $f‘‘‘(x_W) \neq 0$ oder Vorzeichenwechsel von $f‘‘(x)$ in $x_W$
Graph skizzieren	Verwende zum Skizzieren markante Stellen z.B. Nullstellen, Hochpunkte, usw.
Symmetrie	achsensymmetrisch: $f(x)=f(-x)$ punktsymmetrisch: $-f(x)=f(-x)$

Gegeben ist die Funktion $f$ mit $f\left(x\right)=\dfrac{x^2-4}{x^2-1}$ . Ihr Schaubild sei $K_f$ .

Schnittpunkte von $K_f$ mit der $x$ -Achse bestimmen

Schnittpunkt mit der $x$ -Achse:
$f(x)=0$ und nach $x$ auflösen:

Ein Bruch wird Null, wenn sein Zähler Null wird:

$\begin{array}{rll} x^2-4&=&0&\scriptsize{\mid\;+4}\\ x^2&=&4&\scriptsize{\mid\;\sqrt{\;}}\\ x&=&\pm2 \end{array}$

Daraus ergeben sich die Punkte $N_1\left(-2\mid\;0\right)$ und $N_2\left(2\mid\;0\right)$ .

Die senkrechten und waagerechten Asymptoten von $K_f$ bestimmen

$\blacktriangleright$ Senkrechte Asymptoten bestimmen: Nenner gleich Null setzen

Senkrechte Asymptoten liegen an den Definitionslücken von $f$ vor. Diese entsprechen den Nullstellen des Nenners:

$\begin{array}{rll} x^2-1&=&0&\scriptsize{\mid\;+1}\\ x^2&=&1&\scriptsize{\mid\;\sqrt{\;}}\\ x&=&\pm1 \end{array}$

Die senkrechten Asymptoten von $K_f$ haben die Gleichungen $x=-1$ und $x=1$ .

$\blacktriangleright$ Waagerechte Asymptoten bestimmen:

Betrachte den Grenzwert von $f(x)$ für $x\to\infty$ .

$\lim\limits_{x\to\infty}{\dfrac{x^2-4}{x^2-1}}=\dfrac{1-\dfrac{4}{x^2}}{1-\dfrac{1}{x^2}}=\dfrac{1}{1}=1$

Für $x\to\infty$ laufen $\dfrac{4}{x^2}$ und $\dfrac{1}{x^2}$ gegen null, sodass $f(x)$ insgesamt gegen 1 läuft.
Für $x\to-\infty$ ändert sich nichts, da der höchste Exponent jeweils gerade ist. Somit wird alles wieder positiv.

Die waagerechte Asymptote von $K_f$ hat die Gleichung $y=1$ .

Anhand der bisherigen Ergebnisse den Verlauf von $K_f$ in einem Koordinatensystem skizzieren

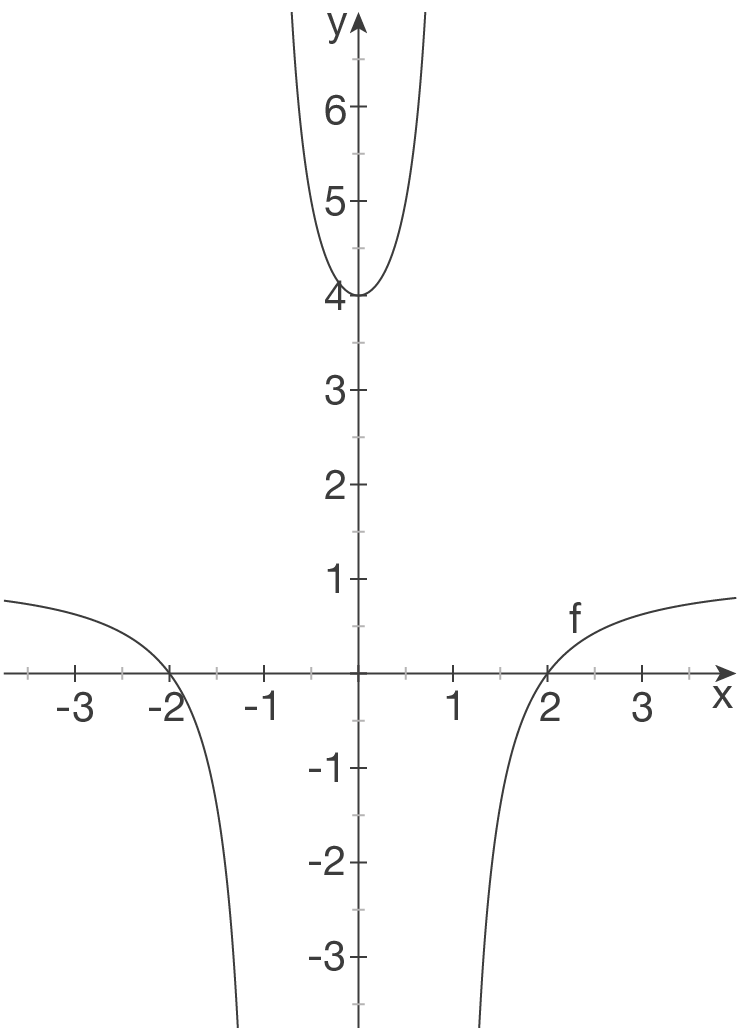
Grafik einer mathematischen Funktion mit einer Parabel im Koordinatensystem.

Prüfen, ob $K_f$ zur $y$ -Achse symmetrisch ist

Behauptung: $K_f$ ist achsensymmetrisch zu $x=0$

Zu zeigen:

$\begin{array}{rll} f\left(x\right)&=&f\left(-x\right) \end{array}$

Beweis:

$\begin{array}{rll} \dfrac{x^2-4}{x^2-1}&=&\dfrac{\left(-x\right)^2-4}{\left(-x\right)^2-1}\\[5pt] \dfrac{x^2-4}{x^2-1}&=&\dfrac{x^2-4}{x^2-1} \end{array}$

Dies ist eine wahre Aussage. Somit ist die Achsensymmetrie zur $y$ -Achse bewiesen.

Nachweisen, dass $f$ an genau einer Stelle die Steigung Null besitzt.
Beschreiben, welche Art von Punkt $K_f$ an dieser Stelle besitzt.

Die Steigung wird dir durch die erste Ableitung $f‘$ gegeben. Zeige also, dass $f‘(x)$ nur genau eine Nullstelle besitzt. Leite $f$ zunächst einmal nach der Quotientenregel ab.

$\begin{array}{rll} f\left(x\right)&=&\dfrac{x^2-4}{x^2-1}\\[5pt] ... \end{array}$

Vollständige Lösung anzeigen

$f‘\left(x\right)=0$ setzen und nach $x$ auflösen:

$\begin{array}{rll} \dfrac{6x}{\left(x^2-1\right)^2}&=&0&\scriptsize{\mid\;\cdot\left(x^2-1\right)^2}\\[5pt] 6x&=&0&\scriptsize{\mid\;:6}\\[5pt] x&=&0\\ \end{array}$

Nur an der Stelle 0 hat $f$ eine Steigung von 0. An dieser Stelle liegt also entweder ein Extremum oder ein Sattelpunkt vor. Prüfe den Wert der zweiten Ableitung an der Stelle $x=0$ , um eine genau Aussage treffen zu können:

$\begin{array}{rll} f‘‘(x)&=&... \end{array}$

Vollständige Lösung anzeigen

Wegen $f‘‘(0)$ = $\dfrac{-6}{(0-1)^3}$ = $\dfrac{-6}{-1}$ = $6>0$ liegt an der Stelle $x=0$ ein Minimum vor.

Gegeben ist die Funktion $f$ mit $f\left(x\right)=\dfrac{x^2+2x-3}{\left(x+1\right)^2}$ .

Schnittpunkte von $K_f$ mit der $x$ -Achse bestimmen

Schnittpunkt mit der $x$ -Achse:
$f(x)=0$ setzen und nach $x$ auflösen:
Ein Bruch wird Null, wenn sein Zähler Null wird:

$\begin{array}{rll} x^2+2x-3&=&0 \end{array}$

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} x_{1,2}&=&-1\pm\sqrt{1+3}\\[5pt] &=&-1\pm2\\[5pt] x_1&=&-3\\[5pt] x_2&=&1 \end{array}$

Daraus ergeben sich die Punkte $N_1\left(-3\mid\;0\right)$ und $N_2\left(1\mid\;0\right)$ .

Die senkrechten und waagerechten Asymptoten von $K_f$ bestimmen

$\blacktriangleright$ Senkrechte Asymptoten bestimmen: Nenner gleich Null setzen

Senkrechte Asymptoten liegen an den Definitionslücken von $f$ vor. Diese entsprechen den Nullstellen des Nenners.

$\begin{array}{rll} \left(x+1\right)^2&=&0&\scriptsize{\mid\;\sqrt{\;}}\\[5pt] x+1&=&0&\scriptsize{\mid\;-1}\\[5pt] x&=&-1 \end{array}$

Die senkrechte Asymptote hat die Gleichung $x=-1$ .

$\blacktriangleright$ Waagerechte Asymptote bestimmen:

Betrachte den Grenzwert von $f(x)$ für $x\to\infty$ .

$\lim\limits_{x\to\infty}{\dfrac{x^2+2x-3}{\left(x+1\right)^2}}=\dfrac{1}{1}=1$

Für $x\to\infty$ läuft $K_f$ gegen 1.
Für $x\to-\infty$ ändert sich nichts, da der höchste Exponent jeweils gerade ist. Somit wird alles wieder positiv.

Die Gleichung der waagerechten Asymptote lautet daher $y=1$ .

Anhand der bisherigen Ergebnisse den Verlauf von $K_f$ in einem Koordinatensystem skizzieren

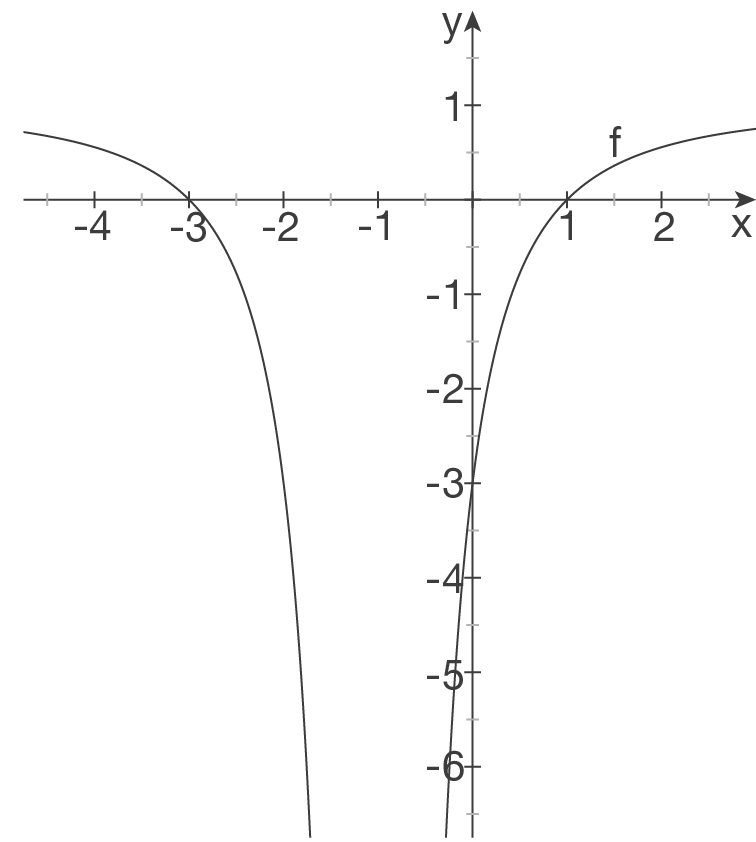
Graph einer Funktion mit x- und y-Achse, zeigt negative Werte und eine Kurve im Bereich der negativen x-Achse.

Beweisen, dass $K_f$ zur senkrechten Asymptote symmetrisch ist

Hier gibt es zwei Lösungswege.

$\blacktriangleright$ Lösungsweg A

Behauptung: $K_f$ ist achsensymmetrisch zu $x=-1$

Zu zeigen:

$\begin{array}{rll} f\left(x+h\right)&=&f\left(x-h\right)\\[5pt] f\left(-1+h\right)&=&f\left(-1-h\right) \end{array}$

Beweis:

$\begin{array}{rll} \dfrac{\left(-1+h\right)^2+...}{\left(-1+h+1\right)^2} \end{array}$

Vollständige Lösung anzeigen

Dies ist eine wahre Aussage. Die Achsensymmetrie zu $x=-1$ ist also bewiesen.

$\blacktriangleright$ Lösungsweg B

Du kannst auch so argumentieren: Wird der Graph der Funktion $f$ um $1$ LE in positive $x$ -Richtung verschoben, so ist er achsensymmetrisch zur $y$ -Achse. Also war ursprünglich achsensymmetrisch zur Geraden $x=-1$ .

Das muss natürlich auch bewiesen werden: Du kannst den Graph von $f$ um $1$ LE in positive $x$ -Richtung verschieben, indem du die Funktionsgleichung änderst. Die verschobene Funktion wollen wir $f_1$ nennen.

$\begin{array}{rll} f_1(x)&=&\dfrac{(x-1)^2+...}{((x-1)+1)^2}\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Wegen $f_1(-x)=\dfrac{(-x)^2-4}{(-x)^2}$ $=\dfrac{x^2-4}{x^2}=f_1(x)$ ist der Graph von $f_1$ achsensymmetrisch zur $y$ -Achse. Also ist der Graph von $f$ achsensymmetrisch zur Geraden $x=-1$ .

Der Funktionsterm von $f$ wird verändert zu $\dfrac{x^2+2x-3}{\left(x+1\right)^2}+x$ . Welche Änderung fällt sofort auf und welche Auswirkungen hat sie auf den Verlauf von $K_f$ ?

Es fällt auf, dass hinter den Bruch noch ein $x$ addiert wird. Das Schaubild von $f$ wird nun also anders verlaufen als vorher. Durch das $x$ besitzt $K_f$ nun eine schiefe Asymptote, keine waagerechte mehr:

$\begin{array}{rll} \lim\limits_{x\to\infty}{\dfrac{x^2+2x-3}{\left(x+1\right)^2}+x}&\\=&\dfrac{1}{1}+\lim\limits_{x\to\infty}{x}\\ \end{array}$

Für $x\to\infty$ nähert sich das Schaubild von $f$ also der Geraden $y=1+x$ an.

Eine weitere Eigenschaft, die sich durch die Modifikation des Funktionsterms verändert, ist die Lage der Nullstellen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?