Stetigkeit
Eine Funktion  ist stetig an der Stelle
ist stetig an der Stelle  , falls gilt
, falls gilt
 oder für
oder für  gilt
gilt  Anschaulich bedeutet das, dass eine Funktion in der Regel stetig ist, wenn sie ohne absetzen zu zeichnen ist. Das ist jedoch nur die vereinfachte Definition und mathematisch nicht ganz korrekt.
Anschaulich bedeutet das, dass eine Funktion in der Regel stetig ist, wenn sie ohne absetzen zu zeichnen ist. Das ist jedoch nur die vereinfachte Definition und mathematisch nicht ganz korrekt.
 mit
mit ![\(D_f= [-1;4]\)](https://www.schullv.de/resources/formulas/73d018a4febbf8cd91e47bae691bc11b909b249168a59dd42d80bbce4075daab_light.svg) ist gegeben. Es wird überprüft, ob
ist gegeben. Es wird überprüft, ob  stetig ist.
stetig ist.

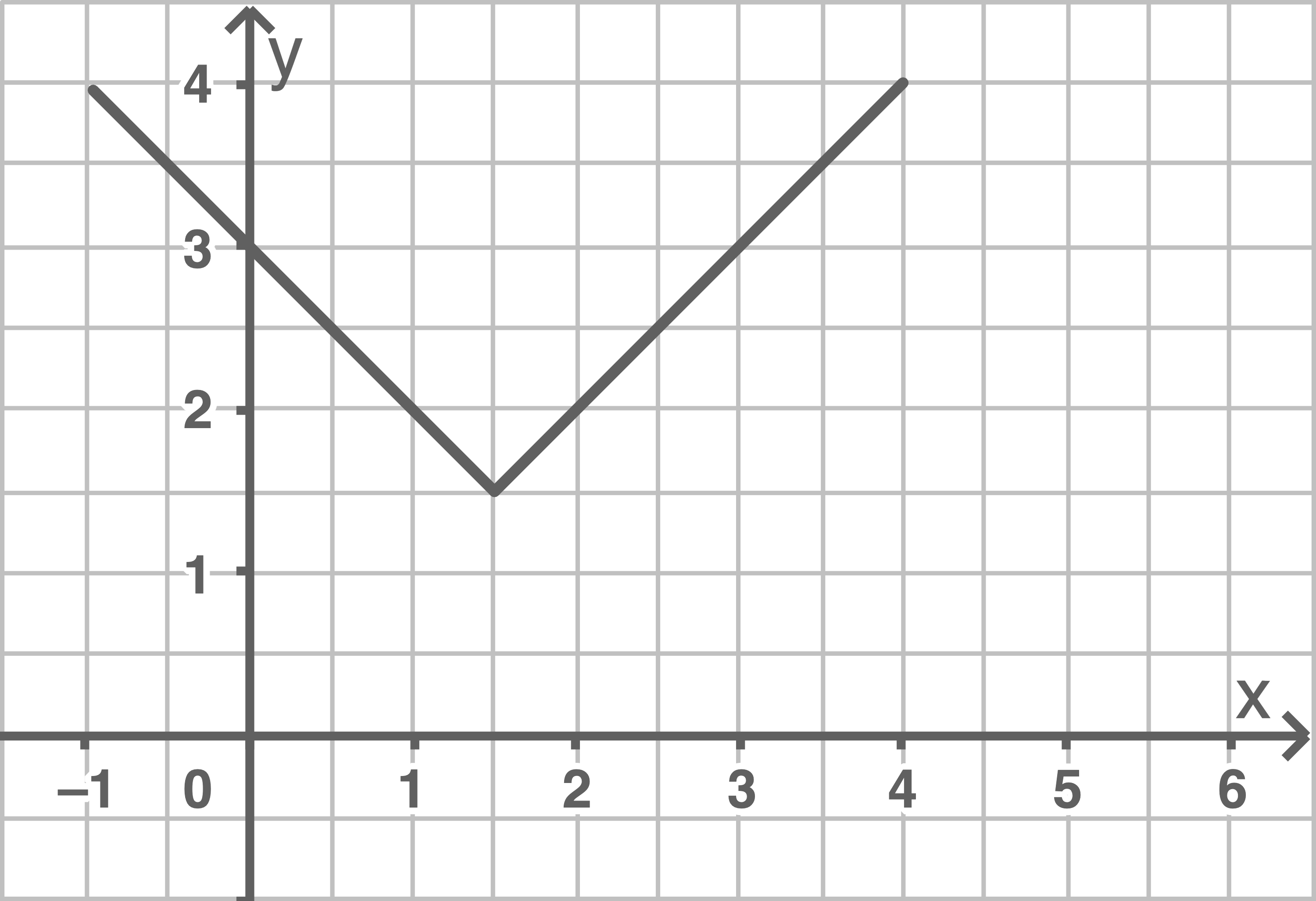 Die Definitionsmenge von
Die Definitionsmenge von  ist in zwei Intervalle zerlegt und in diesen beiden Intervallen jeweils durch einen anderen Funktionsterm festgelegt. Es handelt sich um eine abschnittsweise definierte Funktion.
ist in zwei Intervalle zerlegt und in diesen beiden Intervallen jeweils durch einen anderen Funktionsterm festgelegt. Es handelt sich um eine abschnittsweise definierte Funktion.
 ist in
ist in ![\([-1;1,5]\)](https://www.schullv.de/resources/formulas/9e392ea704301a14de07a3dfb4c007d2a98111c613f04c79b154ed7485edadc7_light.svg) stetig. Ebenso ist auch
stetig. Ebenso ist auch  in
in ![\([1,5; 4]\)](https://www.schullv.de/resources/formulas/d069e4f021fbdac30bd3a5813add48e1117f4fde6aea2718435b74329a4f0723_light.svg) stetig.
Untersucht werden muss also die Stelle
stetig.
Untersucht werden muss also die Stelle  Annäherung von links:
Annäherung von links:

 Annäherung von rechts:
Annäherung von rechts:
 Daraus folgt:
Daraus folgt:
 Die Funktion
Die Funktion  ist somit stetig.
ist somit stetig.
 mit
mit ![\(D_h= [-1,5; 3].\)](https://www.schullv.de/resources/formulas/bfad4b1073cfcfabd7945004b89ca7b27769c69b5a01dec8f4a35cd3421614a8_light.svg)

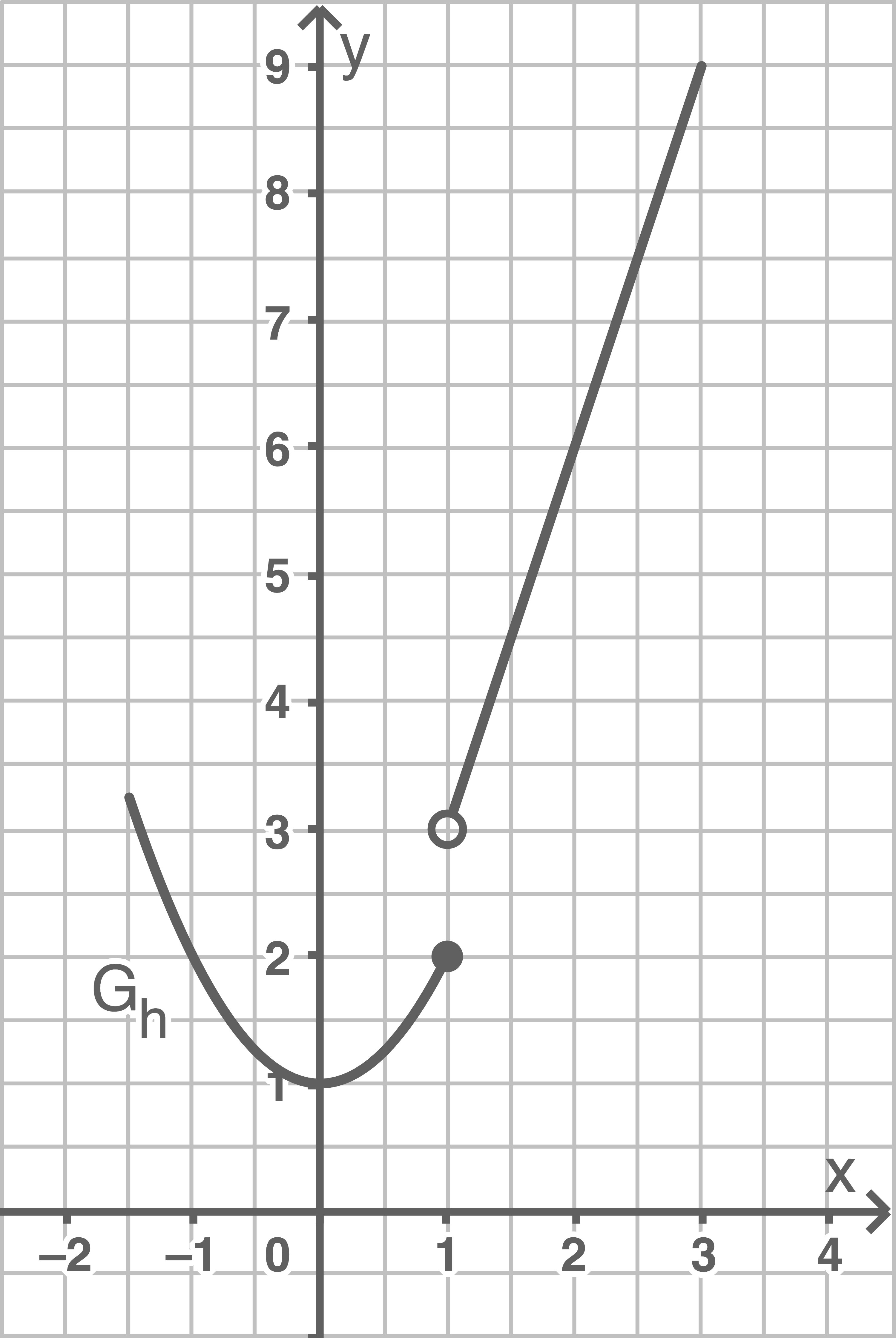
 ist in
ist in ![\([-1,5; 1]\)](https://www.schullv.de/resources/formulas/bd4668b9c4379c12ee71ce363d5ce57cb95bca2d43820fb9265a302093581b58_light.svg) stetig. Auch
stetig. Auch  ist in
ist in ![\([1; 3]\)](https://www.schullv.de/resources/formulas/bc8ca157ae66d2ef930072338329496d0004926d6210460ec63590cb9a490484_light.svg) stetig. Untersucht wird nun die Stelle
stetig. Untersucht wird nun die Stelle  Annäherung von links:
Annäherung von links:
 Annäherung von rechts:
Annäherung von rechts:
 Daraus folgt:
Daraus folgt:
 Die Funktion
Die Funktion  ist somit nicht stetig in
ist somit nicht stetig in  .
.

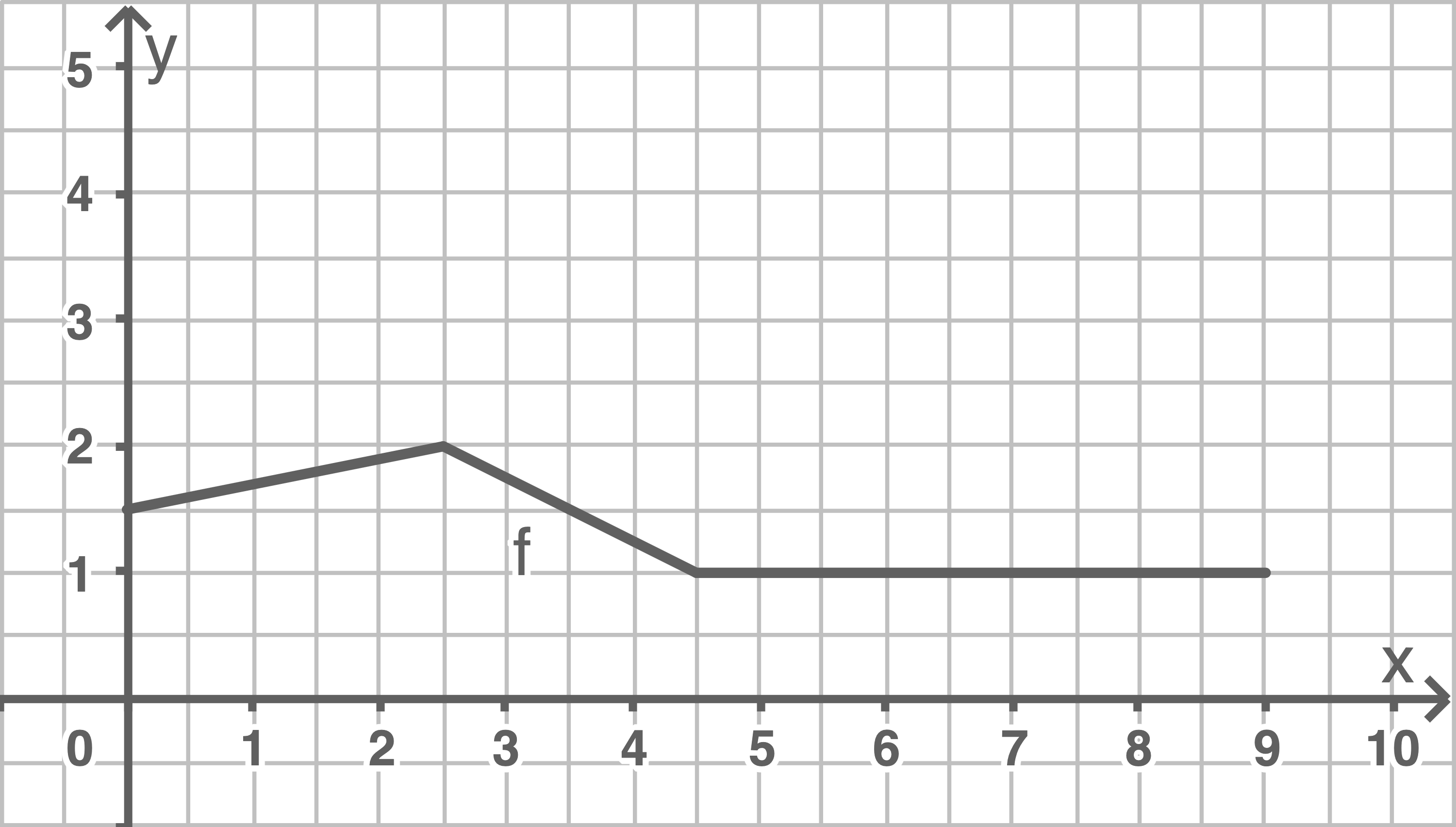
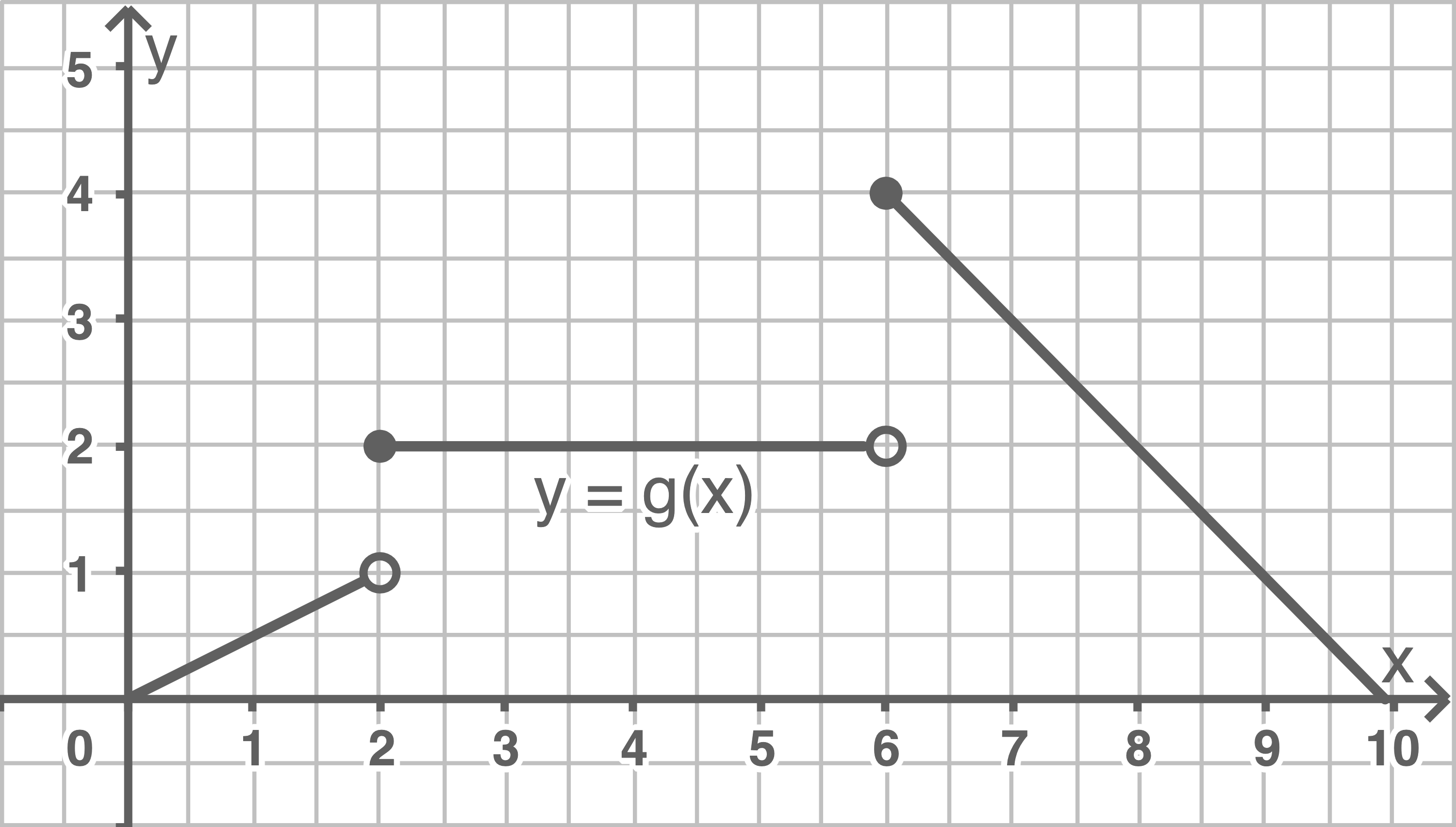
Die Funktion  ist stetig in
ist stetig in ![\([0;9].\)](https://www.schullv.de/resources/formulas/5494b0340897587c679897b3ad9da53f3f4cd85195dd2f87ac5f8f11fb1fa08c_light.svg)

Die Funktion  ist nicht stetig an den Stellen
ist nicht stetig an den Stellen  und
und 
Beispiel 1
Die Funktion
Beispiel 2
Gegeben ist die Funktion
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Eine stetige Funktion enthält keine Lücken in ihrem Definitionsbereich. Sie muss sich ohne absetzen zeichnen lassen.
Beispiel für eine stetige Funktion:
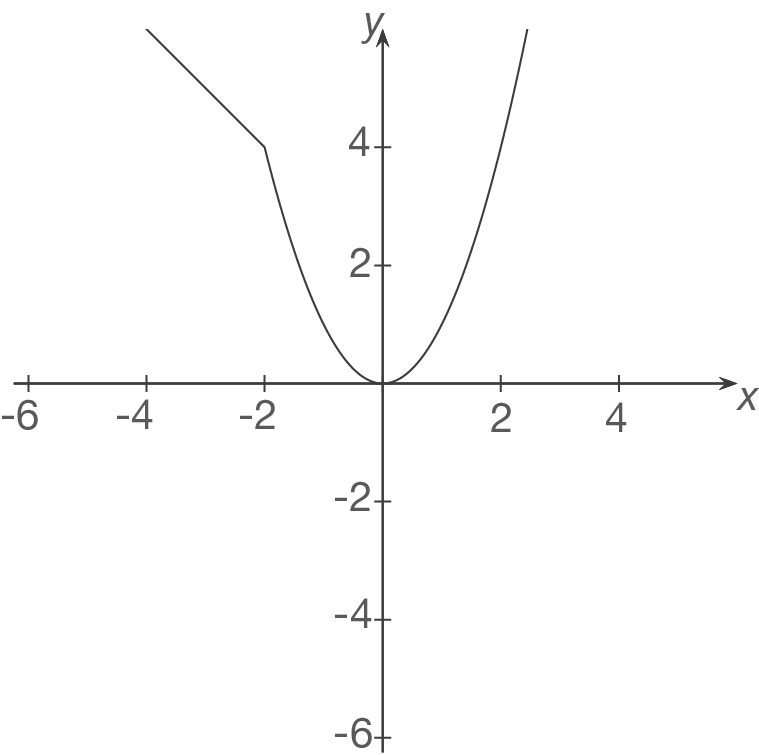

Beispiel für eine nicht stetige Funktion:
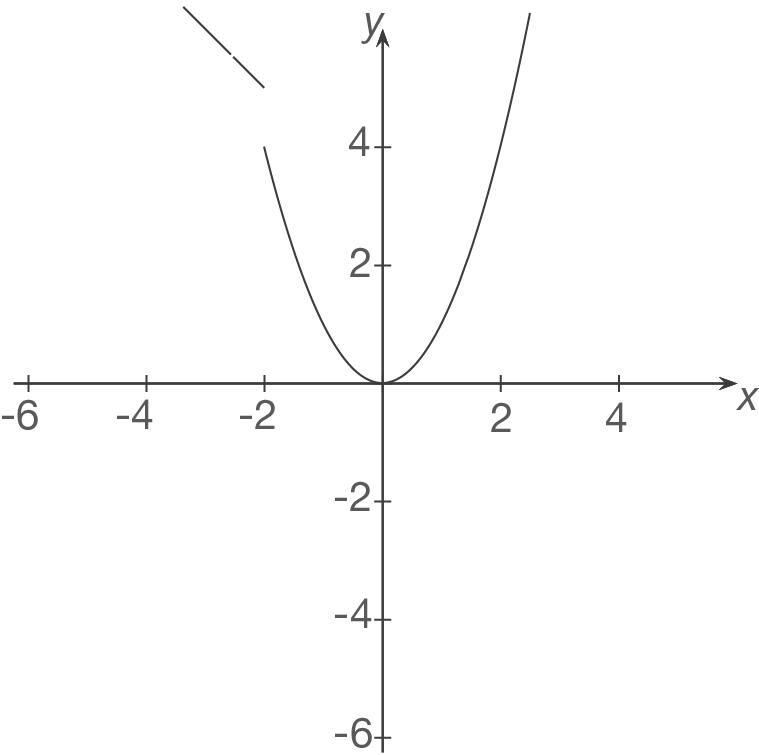

2.
a)
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}ll}
&
\dfrac{1}{2}\cdot2
&
=1
\\
&
4\cdot2-7
&
=1
\end{array}\)](https://www.schullv.de/resources/formulas/8407cde311758dd1d684445ec53d6bc341ed1d632de705565551797659b9de44_light.svg) Die Funktion ist demnach stetig.
Die Funktion ist demnach stetig.
b)
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}ll}
&
\dfrac{1}{3}\cdot3
&
=1
\\
&
2\cdot3-2
&
=4
\end{array}\)](https://www.schullv.de/resources/formulas/ef227555c61d369b990003cb8ea69ede8f79a565aa9a3f20059412001dcb3b3b_light.svg) Die Funktion ist demnach nicht stetig.
Die Funktion ist demnach nicht stetig.
c)
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}ll}
&
(-1)^{2}-2(-1)
&
=3
\\
&
\dfrac{1}{2}(-1)^{2}-\dfrac{5}{2}(-1)
&
=3
\end{array}\)](https://www.schullv.de/resources/formulas/2d37bbd30073cb2fea625b5e56a1a8130f674176a84b03b7d05a9b938a692cbf_light.svg) Die Funktion ist demnach stetig.
Die Funktion ist demnach stetig.