Newtonsches Verfahren

Das Newtonsche Verfahren oder Newtonverfahren, ist ein Verfahren zur näherungsweisen Berechnung der Nullstelle einer differenzierbaren Funktion. Dieses Verfahren ist ein iteratives Verfahren, das heißt, man versucht sich stets der Nullstelle der Funktion mittels Tangenten anzunähern (siehe Skizze).

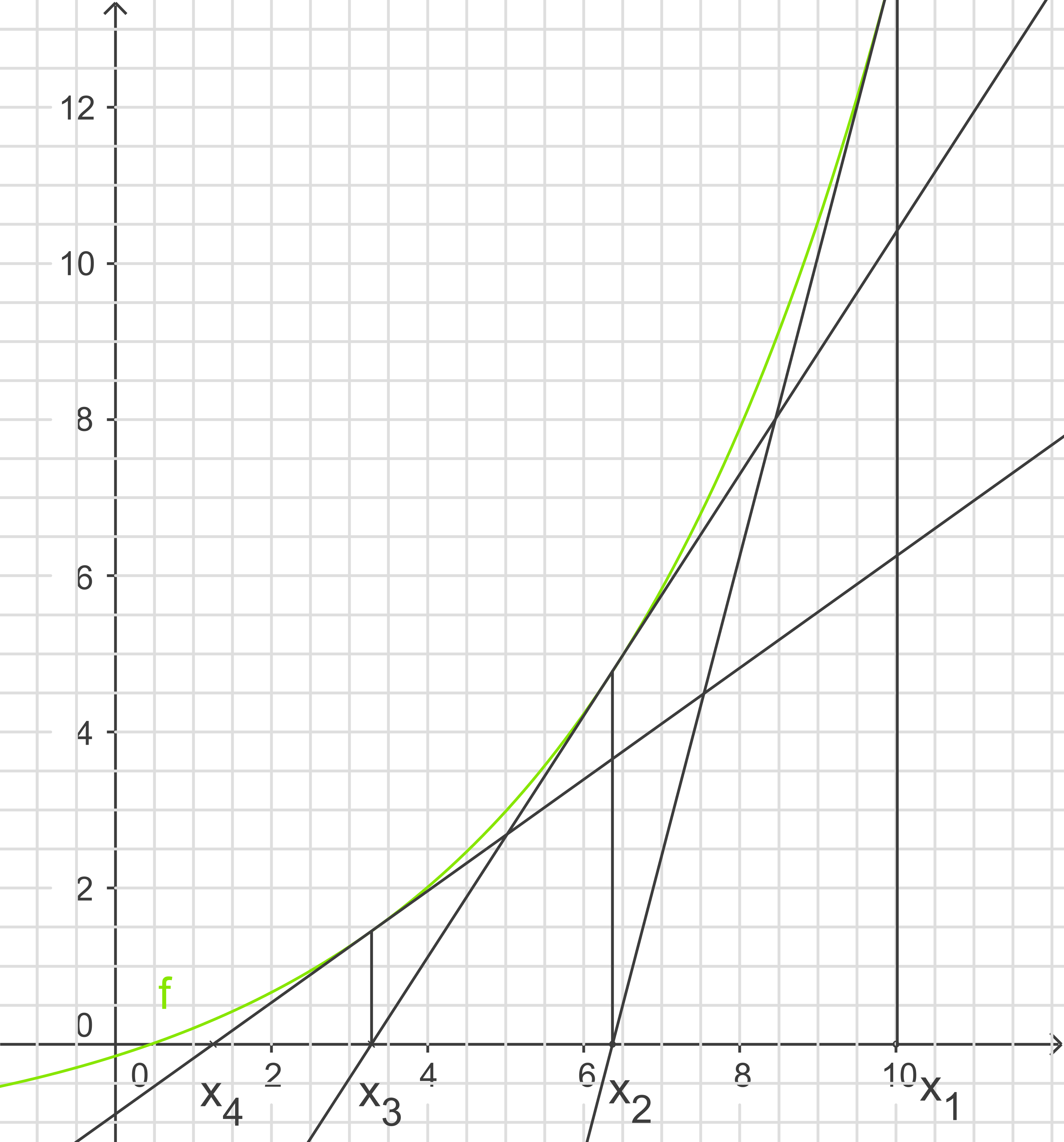
Grafik eines Diagramms mit einer grünen Kurve und gitterförmigem Hintergrund.

Die allgemeine Formel für das Verfahren lautet:

$x_{n+1}=x_n- \dfrac{f(x_n)}{f‘(x_n)}$

Das Verfahren kannst du ausgehend von einem Startwert $x_0$ so lange durchführen, bis die gewünschte Genauigkeit der Nullstelle erreicht ist.
Musst du dir selbst einen Startwert für das Verfahren suchen, so kannst du einfach nach einem Vorzeichenwechsel der Funktion suchen und einen Wert der sich in dessen Nähe befindet als Startwert auswählen.

Beispiel

In diesem Beispiel werden wir die Nullstelle von $f(x)=x^2$ mit Hilfe des Newtonverfahrens annähern. Die Nullstelle von $f(x)$ ist bekanntlich $x=0$ . Wir werden nun ausgehend vom Startwert $x=2$ vier Schritte des Newtonverfahrens durchführen.

Zunächst bestimmen wir die allgemeine Iterationsformel, wozu wir zunächst nur $f‘(x)=2x$ berechnen müssen. Einsetzen von $f(x)$ und $f‘(x)$ liefert dir:

$x_{n+1}=x_n- \dfrac{f(x_n)}{f‘(x_n)}$ $=x_n-\dfrac{x_n^2}{2x_n}=x_n-\dfrac{x_n}{2}$

Für $x_1$ gilt daher nach einsetzen von $x_0$ :

$x_1=x_0-\dfrac{x_0}{2}=2-\dfrac{2}{2}=1$

$x_2=x_1-\dfrac{x_1}{2}=1-\dfrac{1}{2}=\dfrac{1}{2}$

$x_3=x_2-\dfrac{x_2}{2}=\dfrac{1}{2}-\dfrac{\frac{1}{2}}{2}=\dfrac{1}{4}$

$x_4=x_3-\dfrac{x_3}{2}=\dfrac{1}{4}-\dfrac{\frac{1}{4}}{2}=\dfrac{1}{8}$

$\begin{array}[t]{rlll} f\left(x\right)&=x^3+2x-2\\[3pt] f‘\left(x\right)&=3x^2+2 \end{array}$

Startwert: $x_0=2$

Annäherung laut Formel:

$\begin{array}{rlll} x_{n+1}&=x_n-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] x_{n+1}&=x_n-\dfrac{\left(x_n\right)^3+2\cdot x_n-2}{3\left(x_n\right)^2+2} \end{array}$

Da es sehr zeitaufwendig ist, diese Annäherung von Hand durchzuführen und man sich dabei leicht verrechnet, überlassen wir das dem Taschenrechner.
Dazu führen wir nacheinander folgende Schritte aus:

Wir speichern den Startwert $2$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS-(ANS $^3+2\cdot$ ANS-2)/( $3\cdot$ ANS $^2+2$ ).
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*\approx0,7709$

$\begin{array}[t]{rlll} f\left(x\right)&=\dfrac{x+1}{x-2}+1\\[5pt] f‘\left(x\right)&=\dfrac{1\left(x-2\right)-1\left(x+1\right)}{\left(x-2\right)^2}\\[5pt] &=\dfrac{x-2-x-1}{\left(x-2\right)^2}\\[5pt] &=\dfrac{-3}{\left(x-2\right)^2} \end{array}$

Startwert: $x_0=1$

Annäherung laut Formel:

$\begin{array}{rlll} x_{n+1}&=x_n-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] x_{n+1}&=x_n-\dfrac{\dfrac{x_n+1}{x_n-2}+1}{\dfrac{-3}{\left(x_n-2\right)^2}} \end{array}$

Wir speichern den Startwert $1$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS-((ANS+1)/(ANS-2)+1)/((-3)/(ANS-2) $^2$ ).
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*=0,5$

$\begin{array}[t]{rlll} f\left(x\right)&=-x^3+4x^2-1\\[3pt] f‘\left(x\right)&=-3x^2+8x \end{array}$

Startwert: $x_0=4,5$

Annäherung laut Formel:

$\begin{array}{rlll} x_{n+1}&=x_n-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Wir speichern den Startwert $4,5$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS-(-ANS $^3+4$ ANS $^2-1$ )/( $-3\cdot$ ANS $^2+8\cdot$ ANS).
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*\approx3,9354$

$\begin{array}[t]{rlll} f\left(x\right)&=\mathrm e^{2x}+x\\[3pt] f‘\left(x\right)&=2\mathrm e^{2x}+1 \end{array}$

Startwert: $x_0=0$

Annäherung laut Formel:

$\begin{array}{rlll} x_{n+1}&=x_n-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] x_{n+1}&=x_n-\dfrac{\mathrm e^{2x_n}+x_n}{2\mathrm e^{2x_n}+1} \end{array}$

Wir speichern den Startwert $0$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS-(e^{^}( $2\cdot$ ANS)+ANS)/( $2\cdot$ e^{^}( $2\cdot$ ANS)+1).
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*\approx-0,4263$

$\begin{array}[t]{rlll} f\left(x\right)&=x^3-x+6\\[3pt] f‘\left(x\right)&=3x^2-1 \end{array}$

Wir schauen uns das Schaubild der Funktion mit dem GTR an und wählen einen Startwert in der Nähe der Nullstelle:

Startwert: $x_0=-1$

Annäherung laut Formel:

$\begin{array}{rlll} x_{n+1}&=x_n-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] x_{n+1}&=x_n-\dfrac{\left(x_n\right)^3-x_n+6}{3\left(x_n\right)^2-1} \end{array}$

Wir speichern den Startwert $-1$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS-(ANS $^3-$ ANS+6)/(3 $\cdot$ ANS $^2$ -1).
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*=-2$

$\begin{array}[t]{rlll} f\left(x\right)&=\dfrac{2x}{x+2}-1\\[5pt] f‘\left(x\right)&=\dfrac{2\left(x+2\right)-2x}{\left(x+2\right)^2}\\[5pt] &=\dfrac{2x+4-2x}{\left(x+2\right)^2}\\[5pt] &=\dfrac{4}{\left(x+2\right)^2} \end{array}$

Wir schauen uns das Schaubild der Funktion mit dem GTR an und wählen einen Startwert in der Nähe der Nullstelle:

Startwert: $x_0=3$

Annäherung laut Formel:

$\begin{array}{rlll} x_{n+1}&=x_n-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] x_{n+1}&=x_n-\dfrac{\dfrac{2x_n}{x_n+2}-1}{\dfrac{4}{\left(x_n+2\right)^2}} \end{array}$

Wir speichern den Startwert $3$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS-((2 $\cdot$ ANS)/(ANS+2)-1)/((4)/(ANS+2) $^2$ ).
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*=2$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?