Weiterführende Übungsaufgaben
1.
Eine Firma hat ein neues Handy auf dem Markt, das am Anfang sehr schnell und oft verkauft wird.
Als bekannt wird, dass das Handy von einem nicht behebbaren Softwarefehler betroffen ist, bricht der Verkauf sofort ein.
Mit der Funktion lässt sich darstellen, wie viele Handys durchschnittlich pro Woche verkauft wurden.
lässt sich darstellen, wie viele Handys durchschnittlich pro Woche verkauft wurden.
Als bekannt wird, dass das Handy von einem nicht behebbaren Softwarefehler betroffen ist, bricht der Verkauf sofort ein.
Mit der Funktion
a)
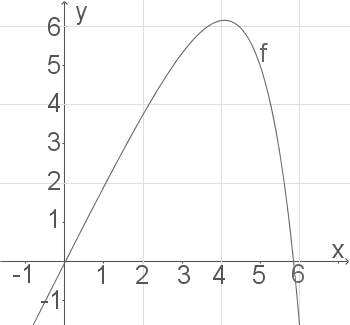
Skizziere das Schaubild von  in einem Koordinatensystem.
Auf der
in einem Koordinatensystem.
Auf der  -Achse soll die Zeit in
Wochen und auf der
-Achse soll die Zeit in
Wochen und auf der  -Achse die Anzahl verkaufter Handys pro Woche abgebildet werden (1 LE
-Achse die Anzahl verkaufter Handys pro Woche abgebildet werden (1 LE  1000 Handys).
1000 Handys).
b)
In welcher Woche wurden die meisten Handys verkauft?
c)
Wie viele Handys wurden in den ersten 5 Wochen insgesamt verkauft?
d)
Wie viele Handys wurden in den ersten 5 Wochen durchschnittlich verkauft?
2.
Ein extra großes Sektglas lässt sich darstellen durch den Rotationskörper, der vom Graphen der Funktion  mit
mit  zwischen
zwischen  und
und  erzeugt wird (der Graph rotiert um die x-Achse).
erzeugt wird (der Graph rotiert um die x-Achse).
a)
Skizziere das Schaubild von  .
.
b)
Bestimme das Volumen des Sektglases (1 VE  1 ml).
1 ml).
c)
Es werden 3ml Sekt eingegossen. Wie hoch steht der Sekt im Glas?
3.
Wir betrachten die Schnittfläche der Funktionen  mit
mit  und
und  mit
mit  . Der Rotationskörper dieser Schnittfläche dient als Modell für einen Rettungsring (Rotation um die x-Achse).
. Der Rotationskörper dieser Schnittfläche dient als Modell für einen Rettungsring (Rotation um die x-Achse).
a)
Skizziere das Schaubild von  und
und  .
.
b)
Der Ring wiegt 50g pro VE; bestimme das Gewicht des Rings.
c)
Wie groß ist der innere Radius des Rings?
d)
Wie breit ist der Ring?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
b)
Hier ist nach dem größten Funktionswert, also nach dem Hochpunkt des Schaubildes gefragt.
Hochpunkt von  bestimmen:
Ableitungen bilden
bestimmen:
Ableitungen bilden
![\(\begin{array}[t]{rlll}
f\left(x\right)&=2x-\dfrac{1}{4}\mathrm e^{x-2}\\[5pt]
f‘\left(x\right)&=2-\dfrac{1}{4}\mathrm e^{x-2}\\[5pt]
f‘‘\left(x\right)&=-\dfrac{1}{4}\mathrm e^{x-2}
\end{array}\)](https://www.schullv.de/resources/formulas/277453185eceeb647460c2916c34b94ecb8c9747cb04faef2ac6ad7b1a51fe22_light.svg)
 setzen
Etwa in der 4. Woche wurden die meisten Handys verkauft.
setzen
Etwa in der 4. Woche wurden die meisten Handys verkauft.
c)
Die Funktion  gibt uns die Anzahl der verkauften Handys pro Woche an. Um die Zahl der Handys berechnen zu können, die bis zur 5. Woche insgesamt verkauft wurden, müssen wir
gibt uns die Anzahl der verkauften Handys pro Woche an. Um die Zahl der Handys berechnen zu können, die bis zur 5. Woche insgesamt verkauft wurden, müssen wir  integrieren.
Integral von x=0 bis x=5 bestimmen
In den ersten 5 Wochen wurden insgesamt etwa 20.000 Handys verkauft.
integrieren.
Integral von x=0 bis x=5 bestimmen
In den ersten 5 Wochen wurden insgesamt etwa 20.000 Handys verkauft.
d)
Um zu berechnen, wie viele Handys durchschnittlich in den ersten 5 Wochen verkauft wurden, bestimmen wir das Integral von  bis
bis  und teilen das Ergebnis durch die Anzahl der Wochen, in diesem Falle also durch 5.
und teilen das Ergebnis durch die Anzahl der Wochen, in diesem Falle also durch 5.
![\(\begin{array}[t]{rlll}
\dfrac{\displaystyle\int_{0}^{5}{f\left(x\right)}\,\mathrm dx}{5}=\dfrac{20}{5}=4
\end{array}\)](https://www.schullv.de/resources/formulas/6240b5cf97ce40f61a51c2e3e1b3834b467319ea39751e1862dd818bbd00c444_light.svg) In den ersten 5 Wochen wurden durchschnittlich je 4000 Handys verkauft.
In den ersten 5 Wochen wurden durchschnittlich je 4000 Handys verkauft.
2.
a)
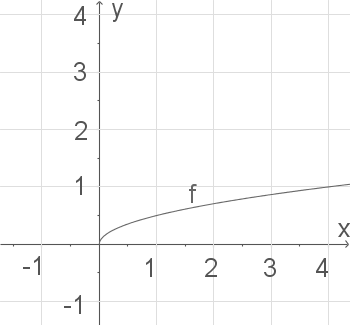
b)
Das Volumen des Sektglases bestimmen wir durch das Volumen des Rotationskörpers.
Volumen des Rotationskörpers berechnen
Das Volumen des Sektglases beträgt etwa 6,28 ml.
c)
Wir haben das Volumen und die untere Grenze  gegeben. Wir wollen also die obere Grenze
gegeben. Wir wollen also die obere Grenze  des Integrals bestimmen.
Da das Sektglas nur von
des Integrals bestimmen.
Da das Sektglas nur von  bis
bis
 dargestellt wird, kommt für uns nur die Lösung
dargestellt wird, kommt für uns nur die Lösung  in Frage.
Wenn 3 ml Sekt eingefüllt werden,
steht dieser im Sektglas etwa 2,76 LE hoch.
in Frage.
Wenn 3 ml Sekt eingefüllt werden,
steht dieser im Sektglas etwa 2,76 LE hoch.
3.
a)

b)
Wir wissen, dass der Ring 50g pro Volumeneinheit wiegt. Wir wissen allerdings nicht, wie groß das Volumen des Rings ist.
Deshalb bestimmen wir zunächst das Volumen des Rotationskörpers.
Als Grenzen des Integrals dienen
hierbei die Schnittpunkte der beiden Kurven.
Volumen des Rotationskörpers bestimmen
Schnittpunkte von f und g bestimmen
Die Grenzen haben wir nun bestimmt.
Da wir den Rotationskörper einer Schnittfläche bestimmen wollen, müssen wir eine Funktion von der anderen abziehen, in diesem Fall rechnen wir  , da
, da  im relevanten Bereich oberhalb von
im relevanten Bereich oberhalb von  liegt.
Volumen berechnen
Das Volumen des Ringes beträgt etwa 98 Volumeneinheiten. Da 1 VE 50g wiegt, wiegt der Ring insgesamt 4.900 g.
liegt.
Volumen berechnen
Das Volumen des Ringes beträgt etwa 98 Volumeneinheiten. Da 1 VE 50g wiegt, wiegt der Ring insgesamt 4.900 g.
V = ...
c)
Wenn wir uns die Skizze ansehen, erkennen wir, dass der innere Radius des Ringes dem  -Wert des Schnittpunktes von
-Wert des Schnittpunktes von  und der
und der  -Achse sein muss.
Inneren Radius des Ringes bestimmen: g(0) berechnen
-Achse sein muss.
Inneren Radius des Ringes bestimmen: g(0) berechnen
![\(\begin{array}[t]{rlll}
g\left(0\right)&=0^2+4\\[3pt]
g\left(0\right)&=4
\end{array}\)](https://www.schullv.de/resources/formulas/401909b60bca33b1983d1cd92870199907601cb9963601c985919e7ee9122f61_light.svg) Der innere Radius des Ringes
beträgt 4 LE.
Der innere Radius des Ringes
beträgt 4 LE.
d)
Die Breite des Ringes ist genau der Abstand zwischen den beiden Schnittpunkten von  und
und  . Dies sind die Punkte, die am weitesten auseinander liegen.
Breite des Ringes bestimmen: Abstand d zwischen den Schnittpunkten ermitteln
. Dies sind die Punkte, die am weitesten auseinander liegen.
Breite des Ringes bestimmen: Abstand d zwischen den Schnittpunkten ermitteln
![\(\begin{array}[t]{rlll}
d&=\dfrac{2}{\sqrt{3}}-\left(-\dfrac{2}{\sqrt{3}}\right)\\[5pt]
&=\dfrac{2}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\\[5pt]
&=\dfrac{4}{\sqrt{3}}\\[5pt]
d&\approx 2,31
\end{array}\)](https://www.schullv.de/resources/formulas/279cfe7254f786df676728918179fdabb0e818c775ae14f6f7e13213cacd82c1_light.svg) Der Ring ist etwa 2,31 LE breit.
Der Ring ist etwa 2,31 LE breit.