Gebrochenrationale Funktionen
Gebrochenrationale Funktionen besitzen ganzrationale Funktionen im Zähler sowie im Nenner, sind also Funktionen der Form:
 Um eine Funktionsgleichung aufzustellen, ist oft folgender Ansatz nützlich, wenn der Graph eine waagerechte Asymptote besitzt:
Um eine Funktionsgleichung aufzustellen, ist oft folgender Ansatz nützlich, wenn der Graph eine waagerechte Asymptote besitzt:
 wobei der Grad von
wobei der Grad von  kleiner als
kleiner als  sein muss.
sein muss.
 entsprechend der waagerechten Asymptote, die dir in der Aufgabenstellung gegeben ist,
entsprechend der waagerechten Asymptote, die dir in der Aufgabenstellung gegeben ist,  ,
,  und
und  entsprechend der Polstellen aus der Aufgabenstellung und
entsprechend der Polstellen aus der Aufgabenstellung und  ,
,  möglichst klein. Beachte dabei folgendes:
möglichst klein. Beachte dabei folgendes:
 und
und  .
Bestimme zum Schluss
.
Bestimme zum Schluss  durch eine Punktprobe.
durch eine Punktprobe.
• Bei einfachen Funktionen ist  (also eine Zahl).
•
(also eine Zahl).
•  ist die Gleichung der waagerechten / schiefen Asymptote oder Näherungskurve.
•
ist die Gleichung der waagerechten / schiefen Asymptote oder Näherungskurve.
•  und
und  sind die Polstellen (Nullstellen des Nenners).
sind die Polstellen (Nullstellen des Nenners).
Wähle für den Ansatz also
• Ist  eine Polstelle mit Vorzeichenwechsel, dann ist
eine Polstelle mit Vorzeichenwechsel, dann ist  ungerade.
• Ist
ungerade.
• Ist  eine Polstelle ohne Vorzeichenwechsel, dann ist
eine Polstelle ohne Vorzeichenwechsel, dann ist  gerade.
gerade.
Gleiches gilt für
1.
Bestimme die Funktionsgleichung und fertige eine Skizze an.
a)
Das Schaubild einer gebrochen-rationalen Funktion hat eine Polstelle ohne VZW (Vorzeichenwechsel) bei  .
Die Gerade
.
Die Gerade  ist die waagerechte Asymptote.
Der Punkt
ist die waagerechte Asymptote.
Der Punkt  liegt auf der Kurve.
liegt auf der Kurve.
b)
Das Schaubild einer gebrochen-rationalen Funktion hat eine Polstelle mit VZW (Vorzeichenwechsel) bei  .
Die Gerade
.
Die Gerade  ist die schiefe Asymptote.
Der Punkt
ist die schiefe Asymptote.
Der Punkt  liegt auf der Kurve.
liegt auf der Kurve.
c)
Das Schaubild einer gebrochen-rationalen Funktion hat zwei Polstellen: Die eine ohne VZW (Vorzeichenwechsel) bei  , die andere mit VZW bei
, die andere mit VZW bei  .
Die Gerade
.
Die Gerade  ist die waagerechte Asymptote.
Der Punkt
ist die waagerechte Asymptote.
Der Punkt  liegt auf der Kurve.
liegt auf der Kurve.
d)
Das Schaubild einer gebrochen-rationalen Funktion hat eine Polstelle ohne VZW (Vorzeichenwechsel) bei  .
Die Gerade
.
Die Gerade  ist die waagerechte Asymptote.
Der Punkt
ist die waagerechte Asymptote.
Der Punkt  liegt auf der Kurve.
liegt auf der Kurve.
2.
Gib jeweils einen möglichen Funktionsterm zur abgebildeten Funktion an.
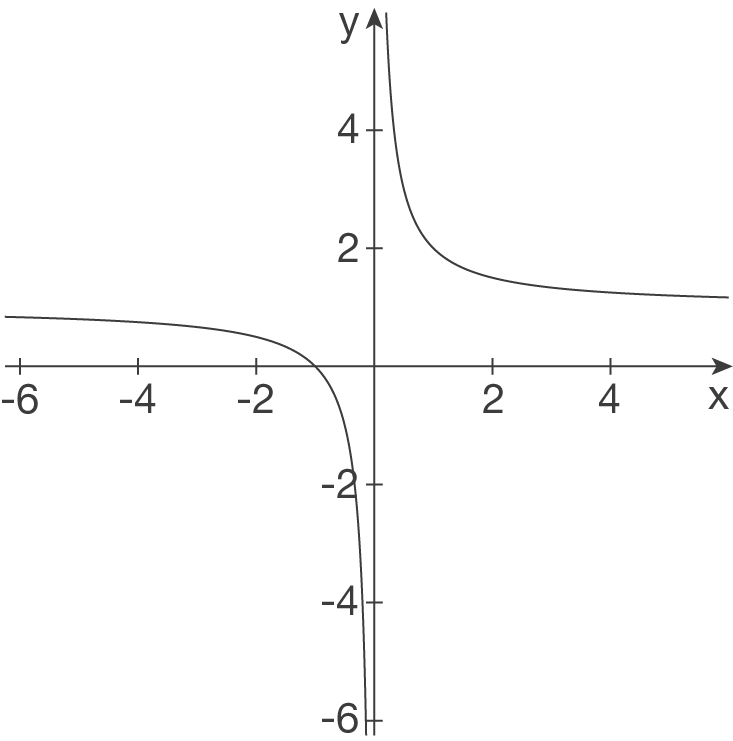 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - Waagerechte Asymptote bei
- Waagerechte Asymptote bei  -
- 
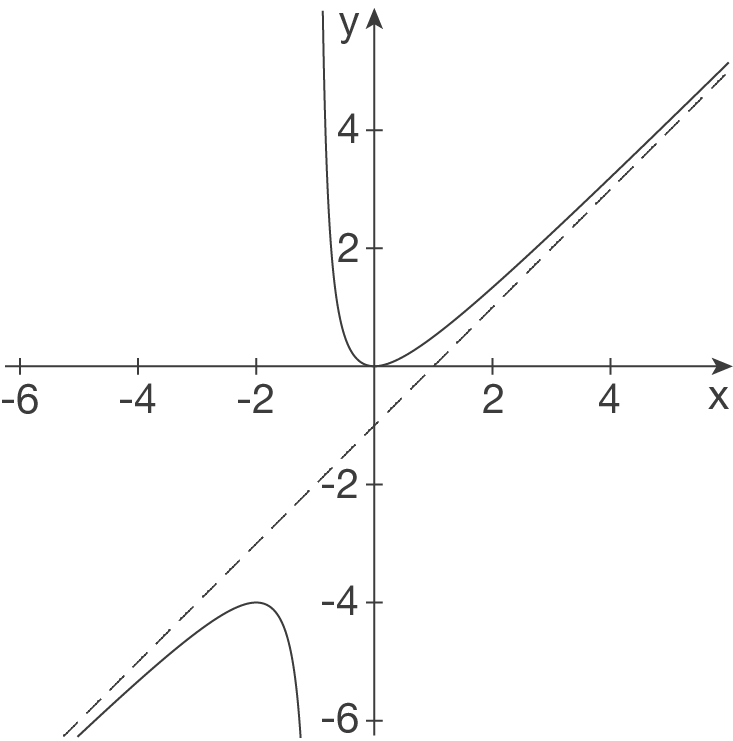 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - Schiefe Asymptote bei
- Schiefe Asymptote bei  -
- 
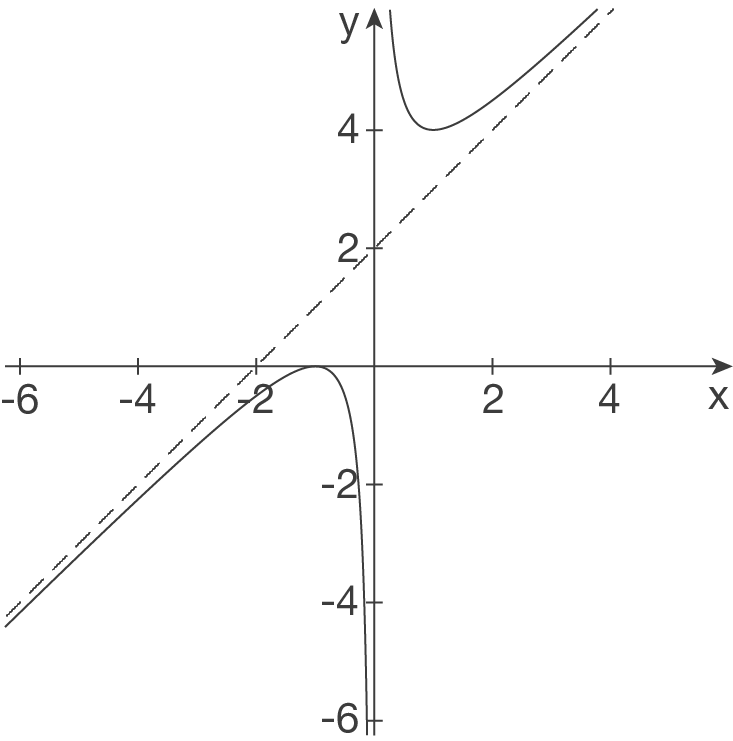 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - Schiefe Asymptote bei
- Schiefe Asymptote bei  -
- 
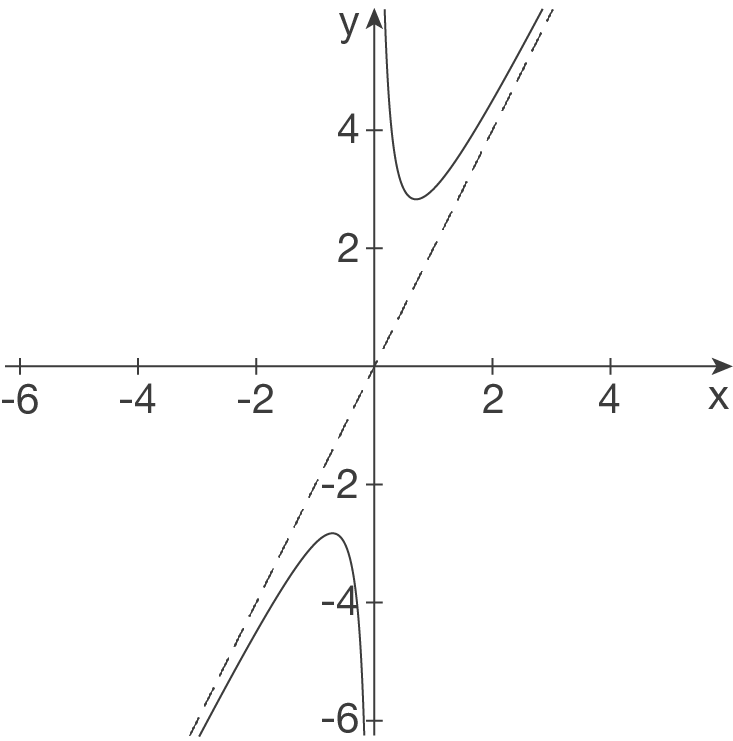 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - Schiefe Asymptote bei
- Schiefe Asymptote bei  -
- 
a)

b)

c)

d)

3.
Gib jeweils einen möglichen Funktionsterm zur abgebildeten Funktion an.
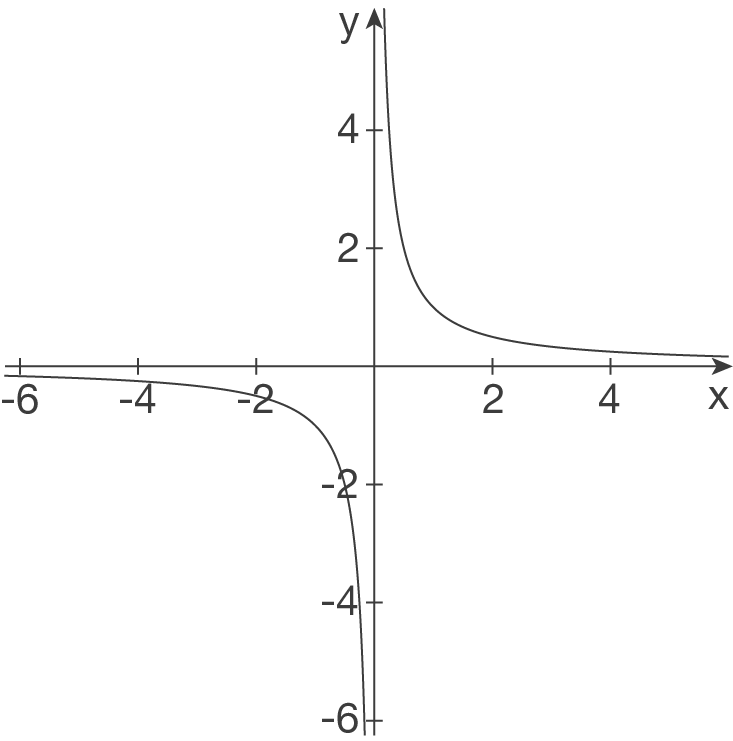 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - waagerechte Asymptote bei
- waagerechte Asymptote bei  -
- 
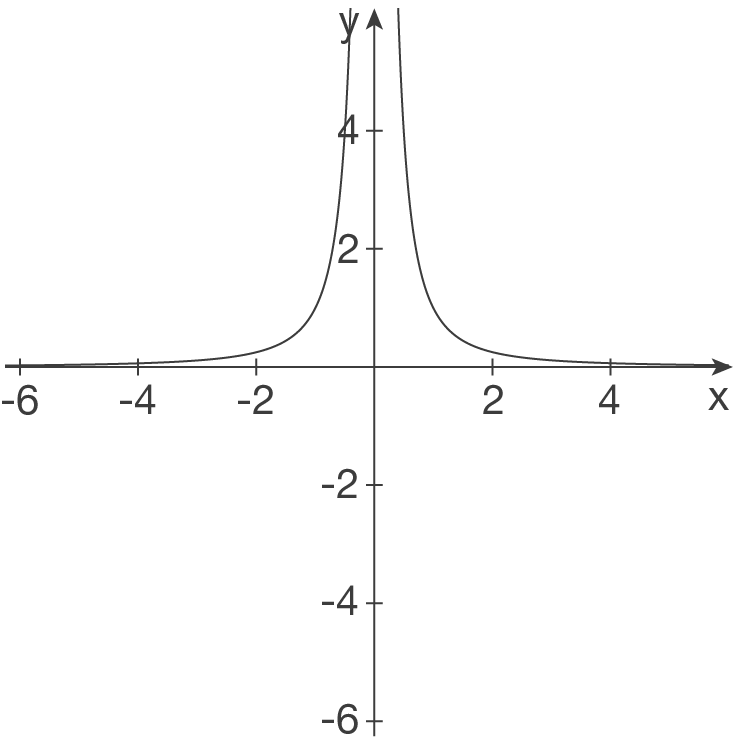 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - waagerechte Asymptote bei
- waagerechte Asymptote bei  -
- 
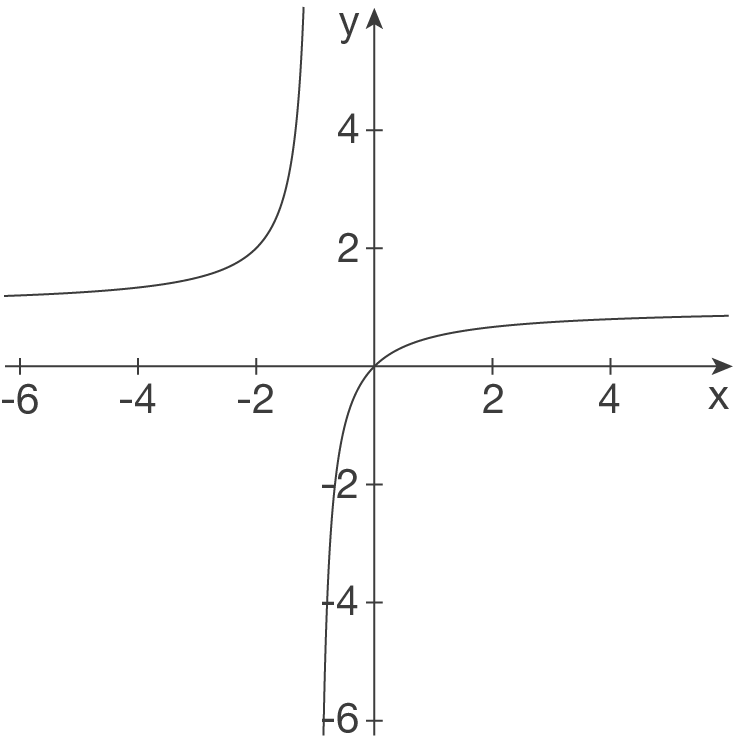 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - waagerechte Asymptote bei
- waagerechte Asymptote bei  -
- 
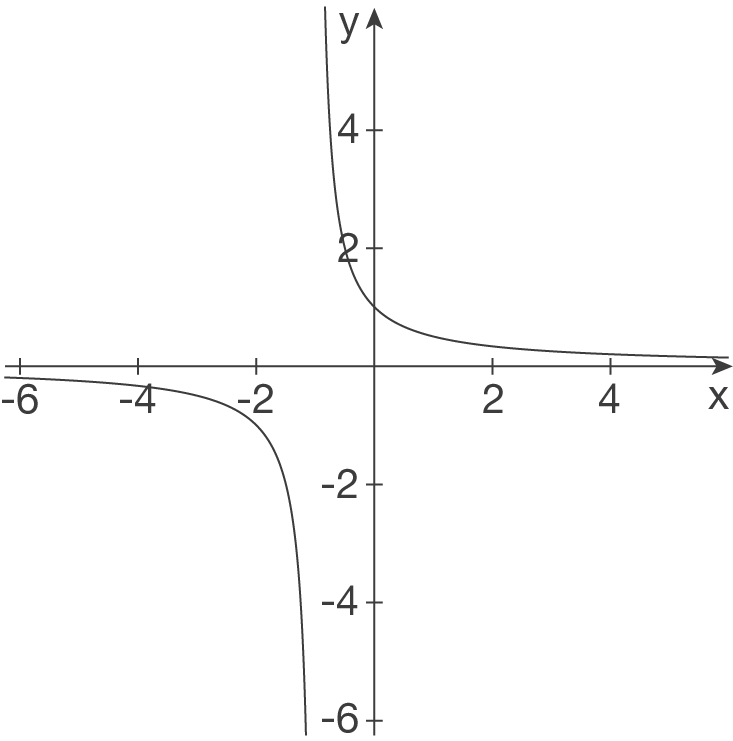 - Senkrechte Asymptote bei
- Senkrechte Asymptote bei  - waagerechte Asymptote bei
- waagerechte Asymptote bei  -
- 
a)

b)

c)

d)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Eine gebrochenrationale Funktionen mit waagrechter / schiefer Asymptote (bzw. Nährungskurve) hat folgenden mögliche Form:
 =
= , wobei der Grad von
, wobei der Grad von  kleiner als
kleiner als  sein muss.
Bei einfachen Funktionen ist
sein muss.
Bei einfachen Funktionen ist
 (also eine Zahl).
(also eine Zahl).
 ist die Gleichung der waagrechten / schiefen Asymptote oder Nährungskurve.
ist die Gleichung der waagrechten / schiefen Asymptote oder Nährungskurve.
 und
und  sind die Polstellen (Nullstellen des Nenners).
sind die Polstellen (Nullstellen des Nenners).
 wird mit Hilfe eines gegeben Punktes bestimmt, indem man diesen einfach in den gemachten Ansatz einsetzt.
wird mit Hilfe eines gegeben Punktes bestimmt, indem man diesen einfach in den gemachten Ansatz einsetzt.
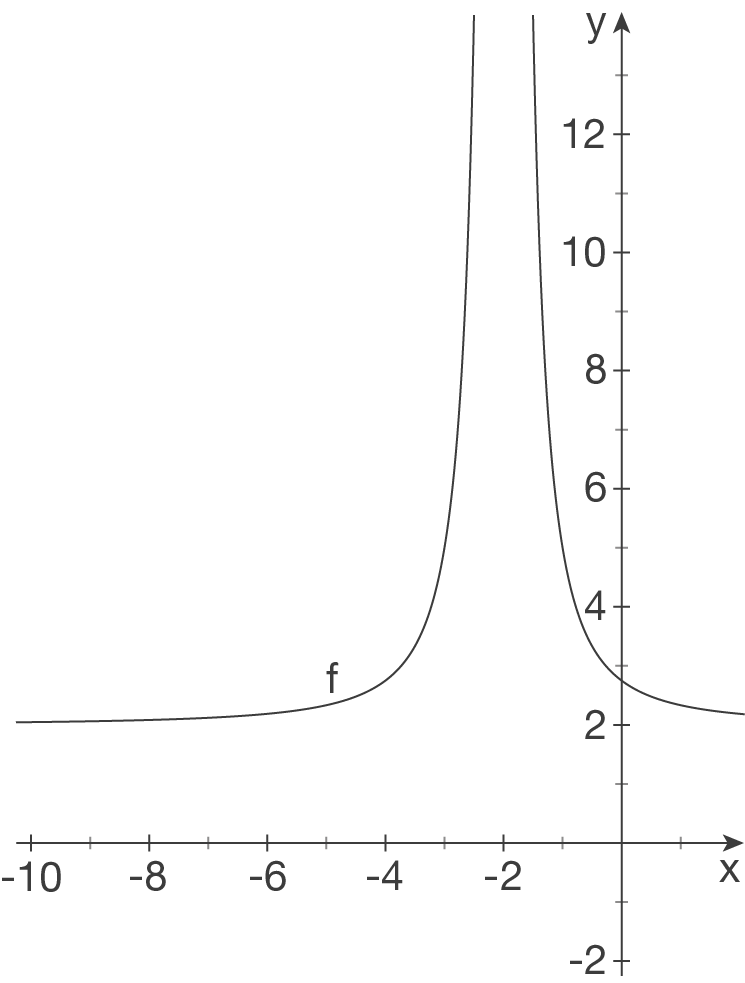
 ,
,  ohne VZW.
ohne VZW.

 (
( )
)

 :
:

 =
=
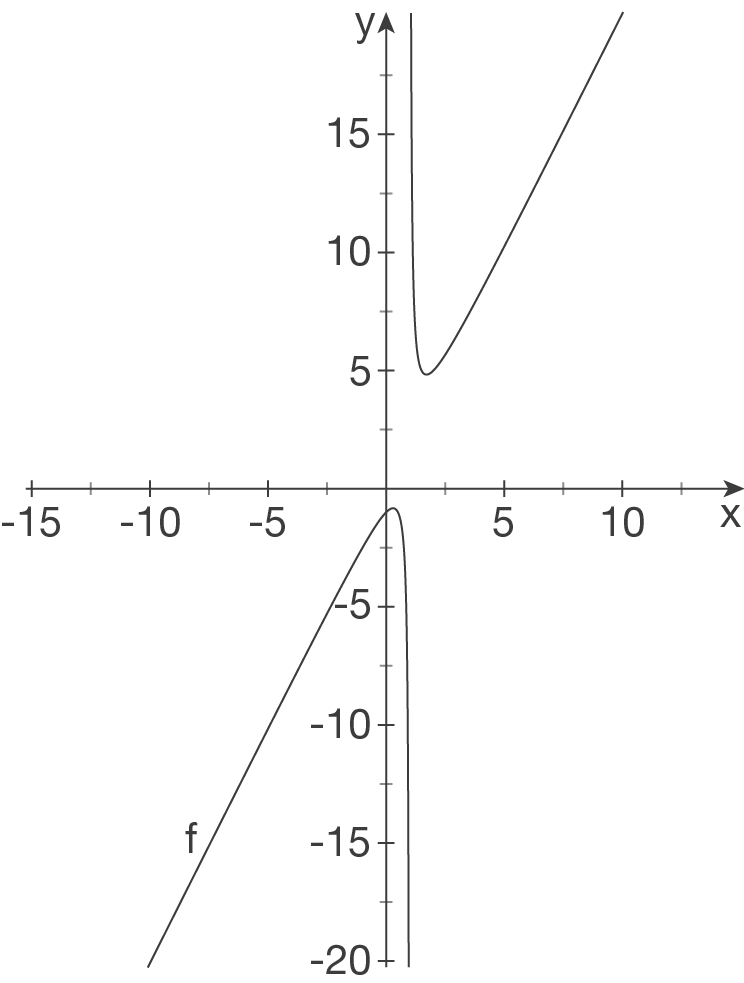
 ,
,  mit VZW.
mit VZW.

 (
( )
)

 :
:

 =
=
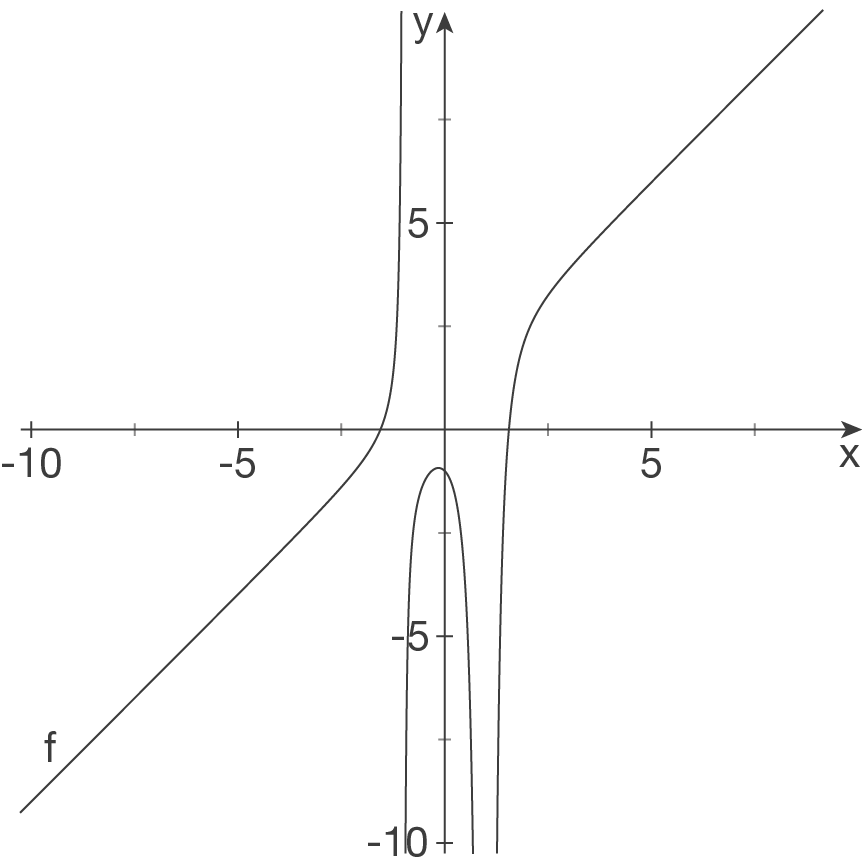
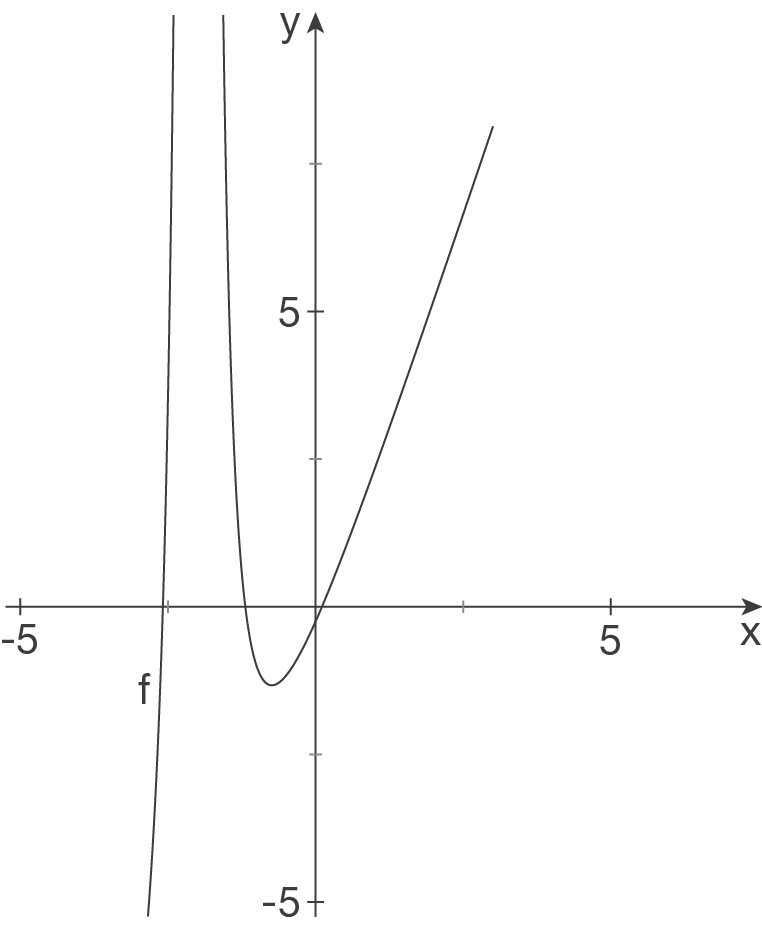
 ,
,  ohne VZW.
ohne VZW.
 =
=
 =
= (
( )
)
 =
=
 :
:


a)

b)

c)

d)

2.
a)
- Polstelle mit VZW an der Stelle
Nenner:
- Waagerechte Asymptote bei
=
(vgl. Punkt
)
=
b)
- Polstelle mit VZW an der Stelle
Nenner:
- Schiefe Asymptote bei
=
(vgl. Punkt
)
=
c)
- Polstelle mit VZW an der Stelle
Nenner:
- Schiefe Asymptote bei
=
(vgl. Punkt
)
=
d)
- Polstelle mit VZW an der Stelle
Nenner:
- Schiefe Asymptote bei
=
(vgl. Punkt
)
=
3.
a)
- Polstelle mit VZW an der Stelle
Nenner:
- Waagerechte Asymptote bei
=
(vgl. Punkt
)
=
b)
- Polstelle ohne VZW an der Stelle
Nenner:
- Waagerechte Asymptote bei
=
(vgl. Punkt
)
=
c)
- Polstelle mit VZW an der Stelle
Nenner:
- Waagerechte Asymptote bei
=
(vgl. Punkt
)
=
=
d)
- Polstelle mit VZW an der Stelle
Nenner:
- Waagerechte Asymptote bei
=
(vgl. Punkt
)
=
=