Ereignisse

Ein Ereignis A ist eine Menge von Ergebnissen, also eine Teilmenge der Ergebnismenge eines Zufallsexperiments. Man spricht davon, dass Ereignis A eintritt, wenn eines der Ergebnisse aus A eintritt.

Gegenereignis

Mit $\overline{A}$ wird das Gegenereignis zu $A$ bezeichnet. Formal gilt: $\overline{A}= \Omega\setminus A$ . Das Gegenereignis enthält also alle möglichen Ergebnisse des Zufallsexperiments aus dem Ergebnisraum, die nicht in $A$ enthalten sind. Das Gegenereignis $\overline{A}$ tritt also genau dann ein, wenn das Ereignis $A$ nicht eintritt.

$P(\overline{A}) = 1- P(A)$

Das Ereignis $B= \Omega$ wird als sicheres Ereignis bezeichnet. Das Ereignis $C = \emptyset$ heißt dagegen unmögliches Ereignis.

Beispiel

Betrachtet wird das 2-malige Werfen einer Münze mit Beachtung der Reihenfolge.

Ereignis $A$ : Es erscheint mindestens einmal „Zahl“
In Mengenschreibweise: $A = \{\text{Zahl-Kopf, Kopf-Zahl, Zahl-Zahl} \}$

$\Rightarrow$ Ereignis $\overline{A}$ : Es erscheint niemals „Zahl“
In Mengenschreibweise: $\overline{A} = \{\text{Kopf-Kopf} \}$

Aus einer Urne mit zwei schwarzen und drei roten Kugeln wird zweimal mit Zurücklegen (und unter Berücksichtigung der Reihenfolge) gezogen.

Gib die Ergebnismenge und folgende Ereignisse in Mengenschreibweise an:

A: „Es wird zweimal eine Kugel der gleichen Farbe gezogen.“

B: „Es wird mindestens einmal eine rote Kugel gezogen.“

Welches der beiden Ereignisse hat die größere Mächtigkeit?

Beim Würfeln mit einem Dodekaeder ist $\Omega=\left\{1;2;3;...11;12\right\}$ .

Beschreibe folgende Ereignisse in Worten:

$A=\{2;4;6;8;10;12\}$

$B=\{1;2\}$

$C=\{2;3;5;7;11\}$

Beim Würfeln ist $\Omega=\left\{1;2;3;4;5;6\right\}$

Gib folgende Ereignisse in Mengenschreibweise an:

A: „Die gewürfelte Zahl ist ungerade.“

B: „Die gewürfelte Zahl ist größer als $2$ , aber kleiner als $6$ .“

C: „Die gewürfelte Zahl ist nicht $3$ .“

Beim Würfeln eines Dodekaeders ist $\Omega=\left\{1;2;3;...11;12\right\}$ , weiterhin sind folgende Ereignisse gegeben:

$A=\left\{3;4;6;12\right\}$ , $B=\left\{1;3;5;7;9;11\right\}$ und $C=\left\{1\right\}$ .

Gib folgende Ereignisse in Mengenschreibweise an:

$A\cap B$

$A\cup B$

$A\cap C$

$A\cup C$

$B\cap C$

$B\cup C$

$\overline{A}\cap B$

$\overline{C}\cup B$

$A\cup B\cup C$

$(A\cap B) \cup C$

$A\cup \emptyset$

$C\cap \emptyset$

Ein Würfel wird zweimal geworfen.

Verknüpfe die Ereignisse mit den Mengensymbolen ( $\cup$ und $\cap$ ) und gib das gesamte Ereignis in Mengenschreibweise an:

A: „Die Summe der zwei Würfe ist größer oder gleich 9 ( $A_1$ ) und es wird keine 6 gewürfelt ( $A_2$ ).“

B: „Es wird genau eine 5 ( $B_1$ ) oder genau eine 4 gewürfelt ( $B_2$ ).“

C: „Es werden zwei gleiche Zahlen gewürfelt ( $C_1$ ) und die Summe der beiden Würfe ist größer oder gleich 8 ( $C_2$ ).“

D: „Es werden zwei gerade Zahlen ( $D_1$ ) und ein Pasch ( $D_2$ ) gewürfelt.“

Welches der Ereignisse hat die größte Mächtigkeit?

Aus einer Urne mit einer roten und einer schwarzen Kugel wird viermal mit Zurücklegen (und unter Berücksichtigung der Reihenfolge) gezogen.

Gib zu den folgenden Ereignissen jeweils die Gegenereignisse in Worten und in Mengenschreibweise an.

A: „Mindestens zwei rote Kugeln werden gezogen.“

B: „Alle gezogenen Kugeln haben die gleiche Farbe.“

C: „Höchstens drei Kugeln sind rot.“

D: „Die zweite und die dritte Kugel sind schwarz.“

In einer Schule stehen fünf mobile Beamer. Folgende Ereignisse seien festgelegt:

$A_i$ : „Der i-te Beamer funktioniert.“ ( $i=1,...,5$ )

B: „Mindestens ein Beamer funktioniert.“

C: „Alle Beamer funktionieren.“

D: „Kein Beamer funktioniert.“

Beschreibe die Ereignisse $B$ , $C$ und $D$ mithilfe der Ereignisse $A_i$ .

Die Ergebnismenge des Zufallsexperiments „Roulettespiel“ ist

$\Omega=\left\{0; 1; 2; 3;... 35; 36\right\}$

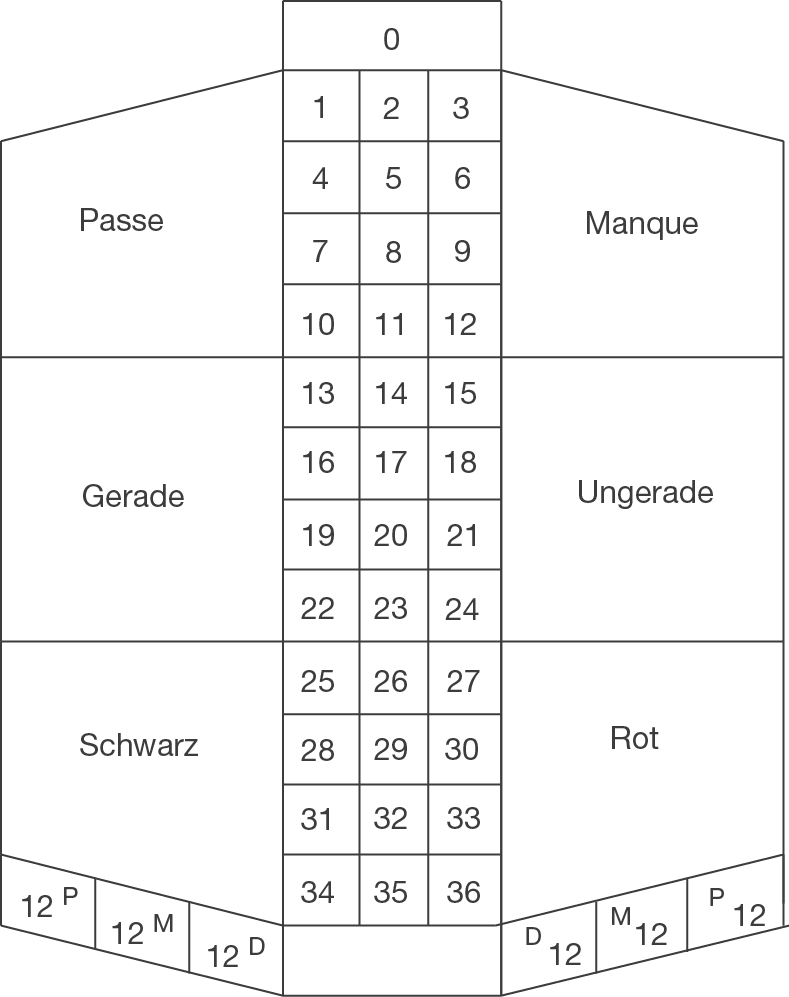Tabelle mit Zahlen und Kategorien wie Passe, Manque, Gerade, Ungerade, Schwarz und Rot.

Wann gewinnt der Spieler?

Schreibe folgende Ereignisse mit den Symbolen der Mengenlehre ( $\cup, \cap,\overline{E_1},\emptyset$ ) und gib die verschiedenen Ergebnismengen an.

A: „Ein Spieler setzt seinen Chip auf das Spielfeld Ungerade und Gerade.“

B: „Ein Spieler setzt seinen Chip auf das Feld $12^P$ (er erwartet also das Fallen einer Zahl aus dem ersten Dutzend) und auf das Feld Gerade.“

C: „Ein Spieler setzt seinen Chip auf $12^P$ und auf die Felder $15;35;0$ .“

D: „Ein Spieler setzt jeweils einen Chip auf alle Primzahlen und auf die Zahl $0$ .“

E: „Ein Spieler setzt einen Chip auf das Feld $1$ , $21$ und $35$ .“

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Mächtigkeit der Ereignisse bestimmen

Ergebnismenge $\Omega=\left\{ss;sr;rs;rr\right\}$

A: „Es wird zweimal eine Kugel der gleichen Farbe gezogen.“
Ereignis $A=\left\{ss;rr\right\}$

B: „Es wird mindestens einmal eine rote Kugel gezogen.“
Ereignis $B=\left\{sr;rs;rr\right\}$

B hat die größere Mächtigkeit, denn: $\left|A\right|=2 < 3=\left|B\right|$

Ereignisse beschreiben

$A=\{2;4;6;8;10;12\}$ : „Es werden nur gerade Zahlen gewürfelt.“

$B=\{1;2\}$ : „Die gewürfelte Zahl ist kleiner als 3.“

$C=\{2;3;5;7;11\}$ : „Die gewürfelte Zahl ist eine Primzahl.“

Ereignisse in Mengenschreibweise angeben

Die Mengenschreibweise für die Ereignisse $A$ , $B$ und $C$ ist:

A: „Die gewürfelte Zahl ist ungerade.“ $A=\left\{1;3;5\right\}$

B: „Die gewürfelte Zahl ist größer als $2$ , aber kleiner als $6$ .“ $B=\left\{3;4;5\right\}$

C: „Die gewürfelte Zahl ist nicht $3$ .“ $C=\left\{1;2;4;5;6\right\}$

Ereignisse in Mengenschreibweise angeben

$A\cap B=\left\{3\right\}$

$A\cup B=\left\{1;3;4;5;6;7;9;11;12\right\}$

$A\cap C=\emptyset$

$A\cup C=\left\{1;3;4;6;12\right\}$

$B\cap C=\left\{1\right\}$

$B\cup C=B$

$\overline{A}\cap B=\ ...$