Vermischte Aufgaben
1.
Gegeben sind die Punkte  ,
,  und
und  .
.
a)
Berechnen Sie die Koordinaten des Bildpunktes  von
von  der bei der Spiegelung an der Geraden durch
der bei der Spiegelung an der Geraden durch  und
und  entsteht.
entsteht.
b)
Bestimmen Sie den Inhalt der Fläche  .
.
c)
Die Fläche  bildet die Grundfläche einer Pyramide, deren Spitze der Ursprung ist. Berechnen Sie das Volumen dieser Pyramide.
bildet die Grundfläche einer Pyramide, deren Spitze der Ursprung ist. Berechnen Sie das Volumen dieser Pyramide.
2.
Gegeben sind die Punkte  ,
,  und
und  , sowie die Gerade
, sowie die Gerade
 :
: 
 .
.
a)
Berechnen Sie die Koordinaten des Schnittpunkts von  und der Ebene
und der Ebene  , welche durch
, welche durch  ,
,  ,
,  aufgespannt wird.
aufgespannt wird.
b)
Die Gerade  entsteht durch Spiegelung der Geraden
entsteht durch Spiegelung der Geraden  an
an  .
Bestimmen Sie eine Gleichung für
.
Bestimmen Sie eine Gleichung für 
3.
Gegeben sind eine Ebene  , sowie zwei Geraden
, sowie zwei Geraden  und
und  .
.  schneidet
schneidet  ,
,  verläuft parallel zu
verläuft parallel zu  .
Sie sollen die Geraden jeweils an
.
Sie sollen die Geraden jeweils an  spiegeln. Beschreiben Sie Ihr Vorgehen.
spiegeln. Beschreiben Sie Ihr Vorgehen.
4.
Zeigen Sie, dass die Gerade
 ,
sowie die Punkte
,
sowie die Punkte  und
und  in einer gemeinsamen Ebene liegen.
Weisen Sie nach, dass
in einer gemeinsamen Ebene liegen.
Weisen Sie nach, dass  der Spiegelpunkt von
der Spiegelpunkt von  an
an  ist.
Kann man generell sagen, dass Punkt, Spiegelgerade und Spiegelpunkt immer in einer Ebene liegen?
ist.
Kann man generell sagen, dass Punkt, Spiegelgerade und Spiegelpunkt immer in einer Ebene liegen?
5.
Gegeben ist der Punkt  und dessen Spiegelpunkt
und dessen Spiegelpunkt  .
Bestimmen Sie die Gleichung einer Spiegelgerade für
.
Bestimmen Sie die Gleichung einer Spiegelgerade für  und
und  , sowie die Gleichung einer Spiegelebene für
, sowie die Gleichung einer Spiegelebene für  und
und  .
.
6.
Die zwei Ebenen  und
und  schneiden sich in einer Geraden. Geben Sie die Koordinaten des Spiegelpunktes von
schneiden sich in einer Geraden. Geben Sie die Koordinaten des Spiegelpunktes von  bezüglich dieser Geraden an.
bezüglich dieser Geraden an.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
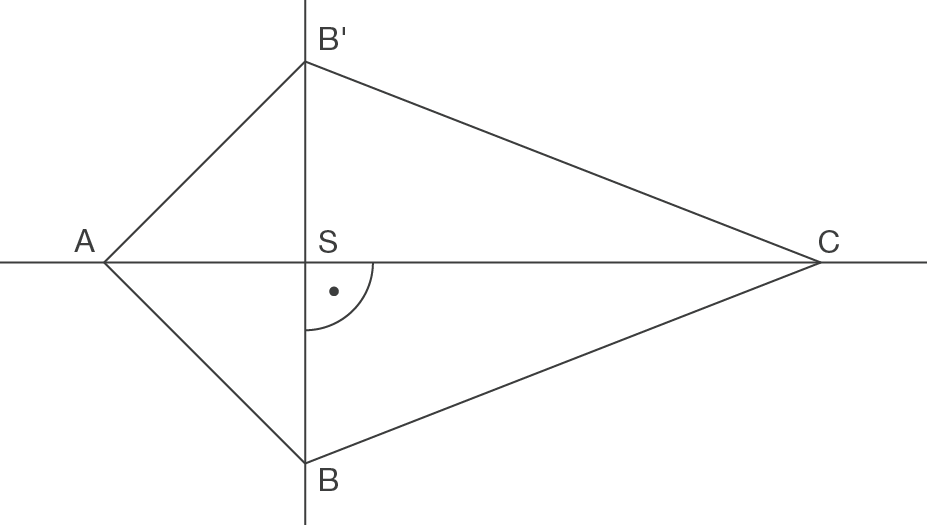
Berechnung des Spiegelpunktes 
 =
= =
= Die Gerade durch die Punkte
Die Gerade durch die Punkte  und
und  hat die Gleichung
hat die Gleichung
 =
= ;
;  Es sei der Punkt
Es sei der Punkt  Fußpunkt des Lotes von
Fußpunkt des Lotes von  auf
auf  .
Dann gilt: Das Skalarprodukt des Vektors
.
Dann gilt: Das Skalarprodukt des Vektors  und des Richtungsvektors
und des Richtungsvektors  der Geraden durch
der Geraden durch  und
und  muss
muss  ergeben
ergeben
 =
= Setzt man
Setzt man  in den Punkt S und den Vektor
in den Punkt S und den Vektor  ein, ergibt sich
ein, ergibt sich  und
und  =
= Für den Spiegelpunkt B‘ gilt:
Für den Spiegelpunkt B‘ gilt:

b)
Bestimmung des Flächeninhalts
c)
Bestimmung des Volumens der Pyramide
Für das Volumen der Pyramide gilt  . Da
. Da  schon in b) berechnet wurde, braucht man noch die Höhe
schon in b) berechnet wurde, braucht man noch die Höhe  der Pyramide. Diese entspricht dem Abstand einer Ebene
der Pyramide. Diese entspricht dem Abstand einer Ebene  durch die Punkte
durch die Punkte  ,
,  ,
,  und
und  zum Ursprung.
Abstand von
zum Ursprung.
Abstand von  zum Koordinatenursprung
Den Normalenvektor
zum Koordinatenursprung
Den Normalenvektor  dieser Ebene
dieser Ebene  bestimmen wir mit Hilfe des Kreuzprodukts der beiden Richtungsvektoren:
Daraus ergibt sich die vorläufige Koordinatengleichung der Ebene:
bestimmen wir mit Hilfe des Kreuzprodukts der beiden Richtungsvektoren:
Daraus ergibt sich die vorläufige Koordinatengleichung der Ebene:
 von
von  :
Einsetzen, des Koordinatenursprungs
:
Einsetzen, des Koordinatenursprungs  liefert
liefert
Das Volumen der Pyramide ist damit
2.
a)
Bestimmung des Schnittpunkts von  und
und  Zunächst bestimmt man eine Parameterform der Ebene
Zunächst bestimmt man eine Parameterform der Ebene  durch die Punkte
durch die Punkte  ,
,  und
und 
 Bestimmung einer Koordinatenform von
Bestimmung einer Koordinatenform von  Für einen Normalenvektor
Für einen Normalenvektor  von
von  gilt
gilt
 und
und 
 und
und 
 Setzt man
Setzt man  , so ergibt sich
, so ergibt sich  und
und  Ein möglicher Normalenvektor ist somit
Ein möglicher Normalenvektor ist somit  Die vorläufige Koordinatenform von
Die vorläufige Koordinatenform von  lautet damit
lautet damit  Setzt man nun noch den Punkt
Setzt man nun noch den Punkt  ein, so ergibt sich
ein, so ergibt sich

 Für den Schnittpunkt von
Für den Schnittpunkt von  und
und  :
:  =
=
 ergibt sich somit
Setzt man nun
ergibt sich somit
Setzt man nun  in
in  ein, so ergibt sich für den Schnittpunkt
ein, so ergibt sich für den Schnittpunkt 
 =
= =
=

b)
Skizze
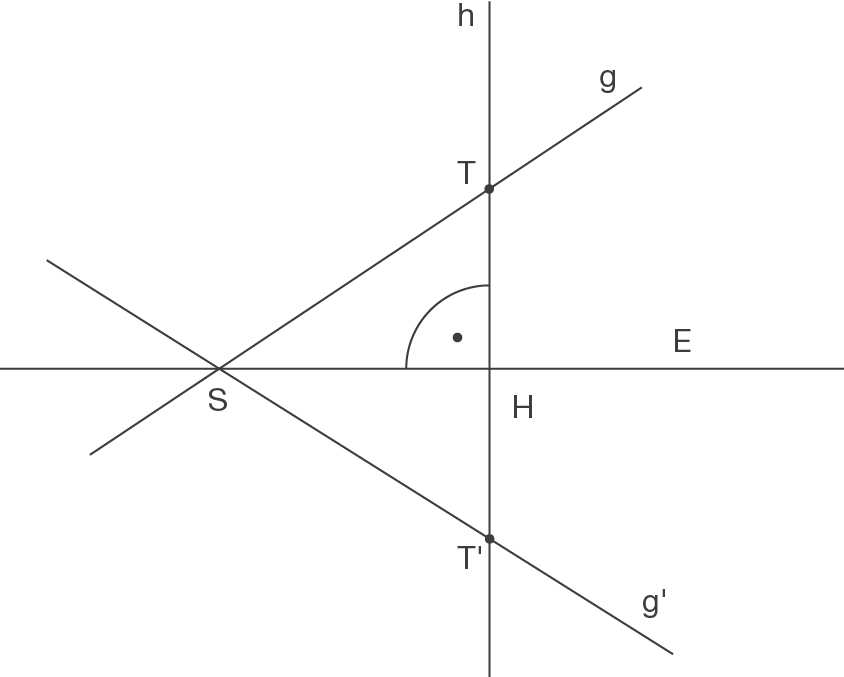 Der Stützvektor
Der Stützvektor  + und damit der Punkt
+ und damit der Punkt  liegt nicht in der Ebene
liegt nicht in der Ebene  , da
, da  :
:  ist.
Um die Gerade
ist.
Um die Gerade  an
an  zu spiegeln reicht es aus, den Punkt
zu spiegeln reicht es aus, den Punkt  an
an  zu Spiegeln und dann die Verbindungsgerade
zu Spiegeln und dann die Verbindungsgerade  von
von  und
und  aufzustellen (siehe Skizze)
Aufstellen der Geraden
aufzustellen (siehe Skizze)
Aufstellen der Geraden  Die Gerade
Die Gerade  steht senkrecht zur Ebene und geht durch den Punkt
steht senkrecht zur Ebene und geht durch den Punkt  .
(der Richtungsvektor von
.
(der Richtungsvektor von  ist der Normalenvektor von
ist der Normalenvektor von  )
)
 =
= Der Schnittpunkt von
Der Schnittpunkt von  und
und  ist
ist  . (
. ( eingesetzt in
eingesetzt in  )
)
 =
=
 Setzt man
Setzt man  in
in  ein, so erhält man
ein, so erhält man  .
Für den Punkt
.
Für den Punkt  gilt
Für die Spiegelgerade
gilt
Für die Spiegelgerade  ergibt sich schließlich
ergibt sich schließlich

3.
Spiegelung von  an
an  beschreiben
beschreiben
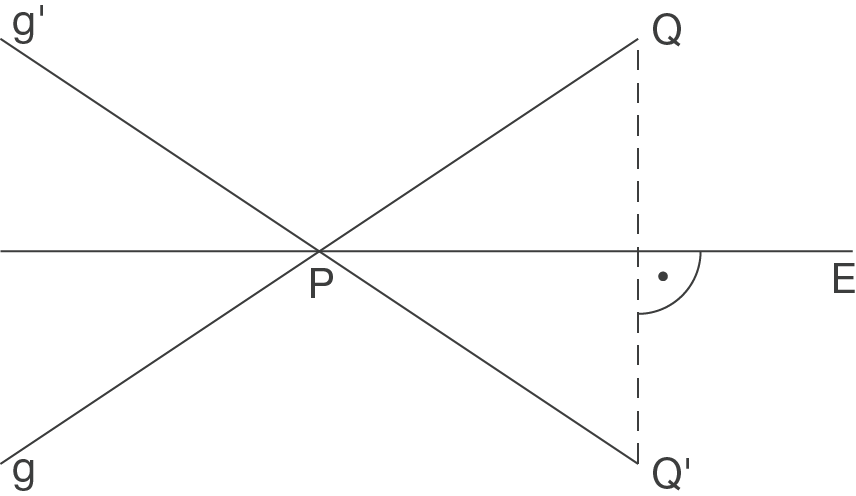 Um die Gleichung einer Geraden bestimmen zu können, benötigen wir zwei Punkte, die auf dieser Geraden liegen. Da
Um die Gleichung einer Geraden bestimmen zu können, benötigen wir zwei Punkte, die auf dieser Geraden liegen. Da  die Spiegelebene
die Spiegelebene  in
in  schneidet, liegt der Punkt
schneidet, liegt der Punkt  auch auf der Spiegelgeraden
auch auf der Spiegelgeraden  .
Wir bestimmen nun einen beliebigen anderen Punkt
.
Wir bestimmen nun einen beliebigen anderen Punkt  der Geraden - dies kann auch der Stützvektor sein, wenn dieser nicht
der Geraden - dies kann auch der Stützvektor sein, wenn dieser nicht  ist - und spiegeln diesen Punkt
ist - und spiegeln diesen Punkt  an der Ebene.
Die Spiegelgerade
an der Ebene.
Die Spiegelgerade  verläuft durch
verläuft durch  und
und  .
Spiegelung von
.
Spiegelung von  an
an  beschreiben
beschreiben
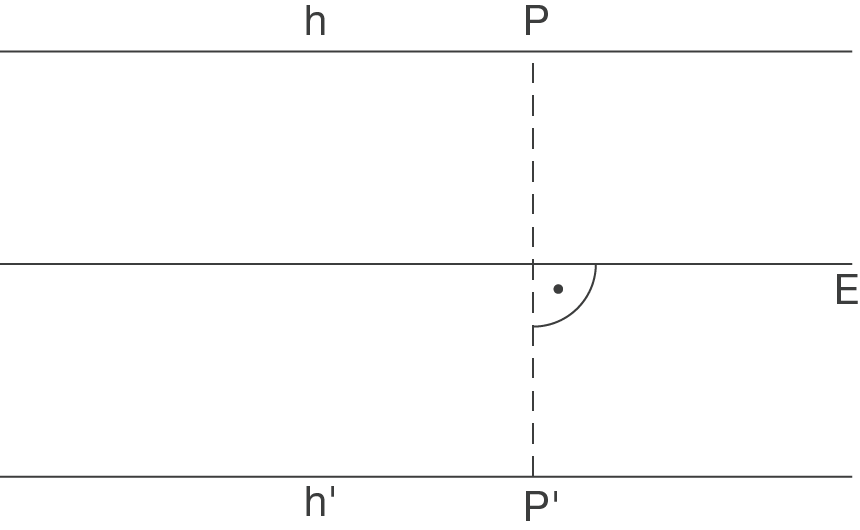
 verläuft parallel zur Ebene
verläuft parallel zur Ebene  ; wenn also
; wenn also  an
an  gespiegelt wird, verläuft die Spiegelgerade
gespiegelt wird, verläuft die Spiegelgerade  immer noch parallel zu
immer noch parallel zu  und insbesondere auch parallel zu
und insbesondere auch parallel zu  .
Wir kennen den Richtungsvektor der Spiegelgeraden also bereits, uns fehlt noch ein Punkt auf
.
Wir kennen den Richtungsvektor der Spiegelgeraden also bereits, uns fehlt noch ein Punkt auf  .
Hierzu wählen wir einen beliebigen Punkt
.
Hierzu wählen wir einen beliebigen Punkt  von
von  und spiegeln diesen an
und spiegeln diesen an  . Die Spiegelgerade
. Die Spiegelgerade  hat den Stützvektor
hat den Stützvektor  und den Richtungsvektor der Geraden
und den Richtungsvektor der Geraden  .
.


4.
Nachweis einer gemeinsamen Ebene
Wir bestimmen zunächst die Gleichung einer Ebene  , in der die Gerade
, in der die Gerade  und der Punkt
und der Punkt  liegen. Anschließend prüfen wir, ob
liegen. Anschließend prüfen wir, ob  ebenfalls in dieser Ebene liegt.
Ebenengleichung aufstellen
Wir benutzen den Stützvektor von
ebenfalls in dieser Ebene liegt.
Ebenengleichung aufstellen
Wir benutzen den Stützvektor von  als Stützvektor von
als Stützvektor von  , den Richtungsvektor von
, den Richtungsvektor von  als ersten Spannvektor von
als ersten Spannvektor von  und den Verbindungsvektor von Stützvektor und
und den Verbindungsvektor von Stützvektor und
 als zweiten Spannvektor.
Punktprobe machen
Wir setzen die Koordinaten von
als zweiten Spannvektor.
Punktprobe machen
Wir setzen die Koordinaten von  für
für  ein.
Wir betrachten die einzelnen Zeilen und es ergibt sich ein lineares Gleichungssystem.
Das Gleichungssystem hat eine eindeutige Lösung,
ein.
Wir betrachten die einzelnen Zeilen und es ergibt sich ein lineares Gleichungssystem.
Das Gleichungssystem hat eine eindeutige Lösung,  liegt in der Ebene
liegt in der Ebene  .
Nachweis des Spiegelpunktes
Wenn
.
Nachweis des Spiegelpunktes
Wenn  der Spiegelpunkt von
der Spiegelpunkt von  an
an  ist, so müssen zwei Bedingungen erfüllt sein:
ist, so müssen zwei Bedingungen erfüllt sein:
 und
und  senkrecht zur Geraden
senkrecht zur Geraden  steht, so müsste das Skalarprodukt von
steht, so müsste das Skalarprodukt von  und dem Richtungsvektor von
und dem Richtungsvektor von  Null ergeben.
Die erste Bedingung ist also erfüllt.
Gleiche Entfernung vom Schnittpunkt nachweisen
Wir bestimmen den Schnittpunkt der Geraden
Null ergeben.
Die erste Bedingung ist also erfüllt.
Gleiche Entfernung vom Schnittpunkt nachweisen
Wir bestimmen den Schnittpunkt der Geraden  durch
durch  und
und  mit
mit  .
Zum Bestimmen des Schnittpunktes setzen wir die Gleichungen der Geraden gleich.
Daraus ergibt sich ein lineares Gleichungssystem.
Um den Schnittpunkt zu bestimmen, setzen wir
.
Zum Bestimmen des Schnittpunktes setzen wir die Gleichungen der Geraden gleich.
Daraus ergibt sich ein lineares Gleichungssystem.
Um den Schnittpunkt zu bestimmen, setzen wir  bzw.
bzw.  in eine der Geradengleichungen ein. Es ergibt sich der Schnittpunkt
in eine der Geradengleichungen ein. Es ergibt sich der Schnittpunkt  Es bleibt zu prüfen, ob
Es bleibt zu prüfen, ob  gleichweit von
gleichweit von  und
und  entfernt ist oder - anders gesagt - ob
entfernt ist oder - anders gesagt - ob  genau der Mittelpunkt zwischen
genau der Mittelpunkt zwischen  und
und  ist:
Damit ist nachgewiesen, dass
ist:
Damit ist nachgewiesen, dass  und
und  Spiegelpunkte bezüglich
Spiegelpunkte bezüglich  sind.
Liegen Punkt, Spiegelpunkt, Spiegelgerade immer in einer Ebene?
Dies ist in der Tat der Fall, versuchen wir es möglichst anschaulich zu begründen:
Im Grunde genommen können wir hier von zwei Geraden sprechen, der Spiegelgerade
sind.
Liegen Punkt, Spiegelpunkt, Spiegelgerade immer in einer Ebene?
Dies ist in der Tat der Fall, versuchen wir es möglichst anschaulich zu begründen:
Im Grunde genommen können wir hier von zwei Geraden sprechen, der Spiegelgerade  und der Geraden
und der Geraden  , die durch
, die durch  und
und  verläuft.
Wenn
verläuft.
Wenn  und
und  Spiegelpunkte bezüglich
Spiegelpunkte bezüglich  sind, wie im Beispiel von eben, so gibt es immer einen Schnittpunkt von
sind, wie im Beispiel von eben, so gibt es immer einen Schnittpunkt von  und
und  .
Da die Geraden sich also schneiden, können sie nicht windschief verlaufen, liegen also nicht in parallelen Ebenen.
Zwei sich schneidende Geraden liegen immer in einer Ebene. Da Punkt und Spiegelpunkt beide auf
.
Da die Geraden sich also schneiden, können sie nicht windschief verlaufen, liegen also nicht in parallelen Ebenen.
Zwei sich schneidende Geraden liegen immer in einer Ebene. Da Punkt und Spiegelpunkt beide auf  liegen, liegen sie somit auch in der Ebene.
liegen, liegen sie somit auch in der Ebene.
- Der Verbindungsvektor von
und
muss senkrecht zur Geraden
stehen
- Der Punkt, in dem die Gerade durch
und
und die Gerade
sich schneiden, muss gleich weit von
und
entfernt sein.
5.
Gleichung einer Spiegelgerade bestimmen
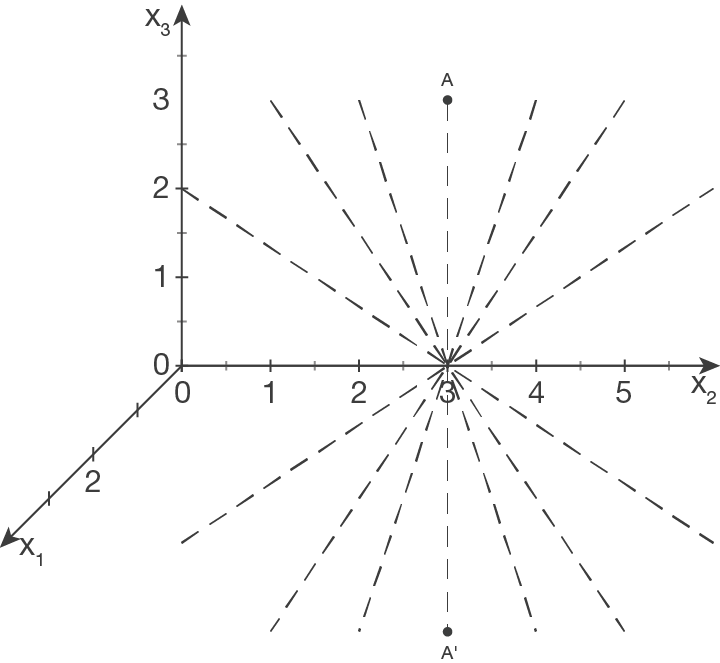 Zunächst müssen wir uns im Klaren darüber sein, dass es unendlich viele Geraden gibt, die Spiegelgeraden für
Zunächst müssen wir uns im Klaren darüber sein, dass es unendlich viele Geraden gibt, die Spiegelgeraden für  und
und  sein können:
Sie liegen alle in der Ebene, deren Stützvektor der Mittelpunkt der Strecke
sein können:
Sie liegen alle in der Ebene, deren Stützvektor der Mittelpunkt der Strecke  ist und die orthogonal zu eben dieser Strecke ist.
Wenn Sie nun also eine andere Spiegelgerade als Lösung erhalten, muss diese nicht notwendigerweise falsch sein.
Für die Spiegelgerade von
ist und die orthogonal zu eben dieser Strecke ist.
Wenn Sie nun also eine andere Spiegelgerade als Lösung erhalten, muss diese nicht notwendigerweise falsch sein.
Für die Spiegelgerade von  und
und  muss - wie bereits gelten:
muss - wie bereits gelten:
 von
von  Richtungsvektor der Geraden bestimmen - orthogonal zu
Richtungsvektor der Geraden bestimmen - orthogonal zu 
 =
= =
= Der Richtungsvektor der Geraden soll orthogonal zu diesem Vektor sein, d.h. das Skalarprodukt der beiden muss Null ergeben. Ein möglicher Vektor wäre somit
Der Richtungsvektor der Geraden soll orthogonal zu diesem Vektor sein, d.h. das Skalarprodukt der beiden muss Null ergeben. Ein möglicher Vektor wäre somit  . Andere Möglichkeiten sind z.B.:
. Andere Möglichkeiten sind z.B.:
 =
= ,
,  =
= , etc.
Eine mögliche Spiegelgerade von
, etc.
Eine mögliche Spiegelgerade von  und
und  wäre also:
wäre also:
 =
= .
Spiegelebene bezüglich
.
Spiegelebene bezüglich  und
und  bestimmen
Für die Spiegelebene gilt:
bestimmen
Für die Spiegelebene gilt:
 =
= .
Die Ebene soll orthogonal zum Vektor
.
Die Ebene soll orthogonal zum Vektor  verlaufen, d.h. der Normalenvektor der Ebene ist parallel zum Vektor
verlaufen, d.h. der Normalenvektor der Ebene ist parallel zum Vektor  . Für unsere Ebene gilt also:
. Für unsere Ebene gilt also:

- Der Stützvektor ist der Mittelpunkt der Strecke
- Sie ist orthogonal zur Geraden durch
und
- Ihr Stützvektor ist der Mittelpunkt der Strecke
- Sie ist orthogonal zum Vektor
6.
Schnittgerade bestimmen
Wir schreiben die Ebenengleichungen untereinander und erhalten ein lineares Gleichungssystem.
Aus  folgt:
folgt:  Einsetzen in
Einsetzen in  liefert:
liefert:
![\(\begin{array}[t]{rll}
6-x_2+2x_3 &=& 6 &\quad \scriptsize \mid\;-6 \\[5pt]
-x_2+2x_3&=& 0 &\quad \scriptsize \mid\; +x_2\\[5pt]
2x_3&=& x_2
\end{array}\)](https://www.schullv.de/resources/formulas/e599658e0c793a0e3d96e6ec527589e5a6b8157d4b97f9da8c00a33d9b431915_light.svg) Wir setzen
Wir setzen  und erhalten:
und erhalten:
 Daraus folgt die Gleichung unserer Geraden:
Daraus folgt die Gleichung unserer Geraden:
 :
: =
= =
= Spiegelpunkt
Spiegelpunkt  bezüglich
bezüglich  bestimmen
Wir fällen das Lot von
bestimmen
Wir fällen das Lot von  auf
auf  . Jeder Punkt
. Jeder Punkt  auf der Geraden
auf der Geraden  hat die Koordinaten
hat die Koordinaten  . Für den Vektor
. Für den Vektor  gilt also allgemein:
gilt also allgemein:
 =
= =
= Dieser Vektor soll orthogonal zur Geraden
Dieser Vektor soll orthogonal zur Geraden  sein, sein Skalarprodukt mit dem Richtungsvektor von
sein, sein Skalarprodukt mit dem Richtungsvektor von  muss also Null ergeben:
muss also Null ergeben:
 Für
Für  ergibt sich
ergibt sich
 und
und  =
= Für den Spiegelpunkt
Für den Spiegelpunkt  gilt also:
Die Koordinaten des Spiegelpunktes
gilt also:
Die Koordinaten des Spiegelpunktes  lauten
lauten  .
.