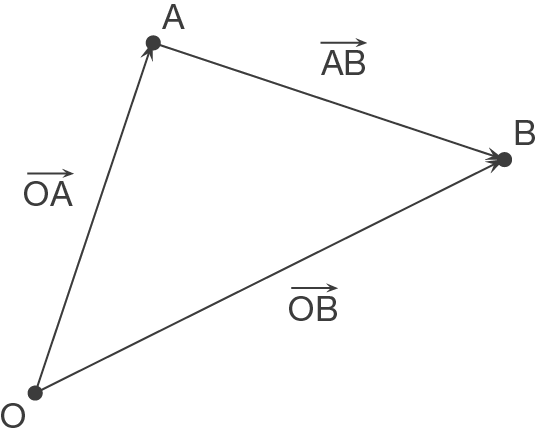
Ortsvektoren und Verbindungsvektoren

Ortsvektoren

Im dreidimensionalen Raum hat ein Punkt $A$ drei Komponenten: $A=(a_1 \mid a_2 \mid a_3 )$ . Dabei entspricht je eine Komponente einer Richtung im Raum. Sind all diese Komponenten gleich Null, so erhält man den Koordinatenursprung $O(0 \mid 0 \mid 0)$ .
Wählst du einen beliebigen Punkt $P(x_1 \mid x_2 \mid x_3)$ im dreidimensionalen Raum, so kannst du einen Vektor $\overrightarrow{p}$ aufstellen, der vom Koordinatenursprung $O(0 \mid 0 \mid 0)$ zum Punkt $P(x_1 \mid x_2 \mid x_3)$ führt:
$\overrightarrow{p}=\overrightarrow{OP}=\begin{pmatrix}x_1\\x_2\\x_3 \end{pmatrix}$
Man nennt einen solchen Vektor Ortsvektor zum Punkt $P$ .

Beispiel

Stelle den Ortsvektor zum Punkt $P(1 \mid 2 \mid 3)$ auf:
$\overrightarrow{p}=\overrightarrow{OP}=\begin{pmatrix}1\\2\\3 \end{pmatrix}$

Verbindungsvektoren

Soll ein Vektor zwei Punkte $A(a_1 \mid a_2 \mid a_3)$ und $B(b_1 \mid b_2 \mid b_3)$ verbinden, so spricht man von einem Verbindungsvektor und schreibt für diesen $\overrightarrow{AB}$ und bestimmt ihn wie folgt:

$\overrightarrow{AB}=\begin{pmatrix}b_1\\b_2\\b_3 \end{pmatrix} - \begin{pmatrix}a_1\\a_2\\a_3 \end{pmatrix} = \begin{pmatrix}b_1-a_1\\b_2-a_2\\b_3-a_3 \end{pmatrix}$

Dieser Vektor zeigt nun von $A$ zu $B$ , umgekehrt zeigt $\overrightarrow{BA}$ von $B$ zu $A$ .

Beispiel

Bestimme einen Verbindungsvektor der Punkte $A(1 \mid 1 \mid 7)$ und $B(3 \mid 4 \mid 3)$ :
$\overrightarrow{AB}=\begin{pmatrix}3\\4\\3 \end{pmatrix} - \begin{pmatrix}1\\1\\7 \end{pmatrix} = \begin{pmatrix}3-1\\4-1\\3-7 \end{pmatrix} = \begin{pmatrix}2\\3\\-4 \end{pmatrix}$

Ortsvektoren und Verbindungsvektoren

Ortsvektoren

Beispiel

Verbindungsvektoren

Beispiel

Weiter lernen mit SchulLV-PLUS!

Weiter lernen mit SchulLV-PLUS!