Flächeninhalt zwischen Graph und Achse
Den Inhalt einer Fläche zwischen einem Graphen und der  -Achse kannst du mit Hilfe von Integralen berechnen.
-Achse kannst du mit Hilfe von Integralen berechnen.
 beschreibt den Inhalt der Fläche, die von dem Graphen zu
beschreibt den Inhalt der Fläche, die von dem Graphen zu  im Bereich
im Bereich  bis
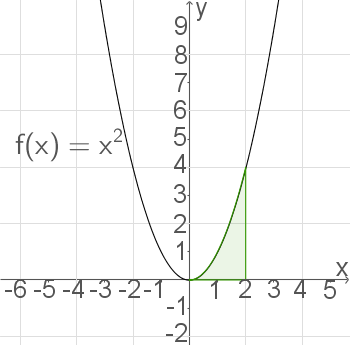
bis  eingeschlossen wird. Im folgenden Bild ist die Fläche grau markiert.
eingeschlossen wird. Im folgenden Bild ist die Fläche grau markiert.
 -Achse bestimmen, so gibt es zwei mögliche Aufgabentypen:
-Achse bestimmen, so gibt es zwei mögliche Aufgabentypen:
Hast du die Grenzen des Bereichs, also und
und  , gegeben, so gehe wie folgt vor:
, gegeben, so gehe wie folgt vor:
 und der
und der  -Achse eingeschlossen wird. Gehe dann wie folgt vor:
-Achse eingeschlossen wird. Gehe dann wie folgt vor:
 mit
mit  mit der
mit der  -Achse einschließt.
Da hier die Grenzen nicht gegeben sind, müssen wir die Nullstellen berechnen. Diese ergeben sich mit
-Achse einschließt.
Da hier die Grenzen nicht gegeben sind, müssen wir die Nullstellen berechnen. Diese ergeben sich mit  ,
,  . Berechne also den Betrag des Integrals über
. Berechne also den Betrag des Integrals über  mit den Nullstellen als Grenzen:
mit den Nullstellen als Grenzen:

 mit
mit  und der
und der  -Achse im Bereich
-Achse im Bereich  bis
bis  .
Die Nullstellen sind hier
.
Die Nullstellen sind hier  ,
, und
und  . Hier musst du also zwei Integrale berechnen:
. Hier musst du also zwei Integrale berechnen:
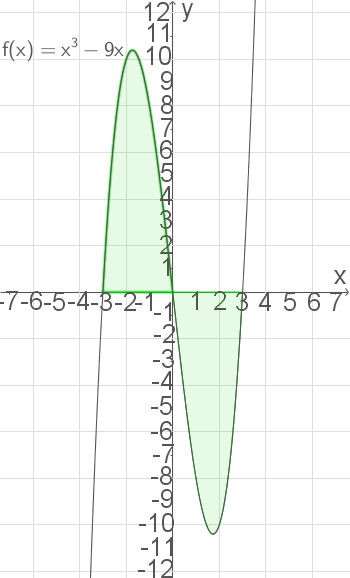
Auf dem folgenden Bild sind die beiden Teilflächen dargestellt:
Beispiel
Das Integral
Vorgehen
Sollst du den Inhalt einer Fläche zwischen einem Graphen und derHast du die Grenzen des Bereichs, also
- Überprüfe, ob zwischen den beiden Grenzen
und
eine oder sogar mehrere Nullstellen von
liegen.
-
- Gibt es keine Nullstellen im angegebenen Intervall, so berechne das Integral über
in den Grenzen
und
. Nimm am besten immer den Betrag des Integrals. Denn wenn die Fläche unterhalb der
-Achse liegt, hat das Integral ein negatives Vorzeichen, Flächeninhalte sind aber immer positiv.
- Gibt es Nullstellen, so musst du mehrere Integrale über
berechnen: Das Integral von der unteren Grenze
bis zur ersten Nullstelle, das Integral von der ersten Nullstelle bis zur zweiten Nullstelle,... , das Integral von der letzten Nulltelle bis zur oberen Grenze
. Zum Schluss musst du die Beträge addieren.
- Gibt es keine Nullstellen im angegebenen Intervall, so berechne das Integral über
- Bestimme die Nullstellen von
. In solchen Fällen gibt es meist genau zwei.
- Berechne das Integral über
mit den Nullstellen als Grenzen. Gibt es doch mehr als zwei Nullstellen, so musst du auch hier von Nullstelle zu Nullstelle integrieren und alle Beträge addieren.
Beispiel 1
Bereche den Inhalt der Fläche, den die FunktionBeispiel 2
Berechne den Inhalt der Fläche zwischen dem Graphen vonAuf dem folgenden Bild sind die beiden Teilflächen dargestellt:

1.
Berechne den Flächeninhalt der Fläche, die von der  -Achse und dem Graphen der Funktion
-Achse und dem Graphen der Funktion  innerhalb der angegebenen Grenzen eingeschlossen wird.
innerhalb der angegebenen Grenzen eingeschlossen wird.

 ,
, 

 ,
, 

 ,
, 

 ,
, 
a)
b)
c)
d)
2.
Berechne den Flächeninhalt der Fläche, welche von der  -Achse und dem Graphen der Funktion
-Achse und dem Graphen der Funktion  vollständig eingeschlossen wird.
vollständig eingeschlossen wird.




a)
b)
c)
d)
3.
Gegeben ist die Funktion  und eine untere Grenze
und eine untere Grenze  . Bestimme die obere Grenze
. Bestimme die obere Grenze  so, dass der Inhalt der Fläche, die von der
so, dass der Inhalt der Fläche, die von der  -Achse und dem Graphen der Funktion
-Achse und dem Graphen der Funktion  innerhalb der Grenzen
innerhalb der Grenzen  und
und  eingeschlossen wird, den angegebenen Wert annimmt.
eingeschlossen wird, den angegebenen Wert annimmt.

 ,
,  FE
FE
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
b)
c)
d)
2.
a)
1. Schritt: Intervall bestimmen
Berechne zunächst die Nullstellen der Funktion  , um die Grenzen der Integration zu ermitteln. Setze dazu
, um die Grenzen der Integration zu ermitteln. Setze dazu  .
Ein Produkt ist Null, wenn einer seiner Faktoren Null ist:
.
Ein Produkt ist Null, wenn einer seiner Faktoren Null ist:
 ;
;  Es folgt das Intervall
Es folgt das Intervall ![\(I = [0;2]\)](https://www.schullv.de/resources/formulas/2a26ff8c733b42249cc675b4ec602daa943b6321d5d34019d221590b672f4103_light.svg) .
2. Schritt: Integral berechnen
.
2. Schritt: Integral berechnen
b)
1. Schritt: Intervall bestimmen
Berechne zunächst die Nullstellen der Funktion  , um die Grenzen der Integration zu ermitteln. Setze dazu
, um die Grenzen der Integration zu ermitteln. Setze dazu  .
Ein Produkt ist Null, wenn einer seiner Faktoren Null ist:
.
Ein Produkt ist Null, wenn einer seiner Faktoren Null ist:
 ;
;  Es folgt das Intervall
Es folgt das Intervall ![\(I = [0;4]\)](https://www.schullv.de/resources/formulas/f66e4f3e1636381bad48686fac58ada39caaafd4e532effa5f44916047de8b94_light.svg) .
2. Schritt: Integral berechnen
.
2. Schritt: Integral berechnen
c)
1. Schritt: Intervall bestimmen
Berechne zunächst die Nullstellen der Funktion  , um die Grenzen der Integration zu ermitteln. Setze dazu
, um die Grenzen der Integration zu ermitteln. Setze dazu  .
.
 Berechne die Nullstellen von
Berechne die Nullstellen von  mit der
mit der  -Formel:
Es folgt damit das Intervall
-Formel:
Es folgt damit das Intervall ![\(I = [2;5]\)](https://www.schullv.de/resources/formulas/b647df5d32bf8568d44ac58141a8467dd98a5e9da232501e08be1ee045ae13f4_light.svg) .
2. Schritt: Integral berechnen
.
2. Schritt: Integral berechnen
d)
1. Schritt: Intervall bestimmen
Berechne zunächst die Nullstellen der Funktion  , um die Grenzen der Integration zu ermitteln. Setze dazu
, um die Grenzen der Integration zu ermitteln. Setze dazu  .
.
 Ein Produkt ist Null, wenn einer seiner Faktoren Null ist:
Ein Produkt ist Null, wenn einer seiner Faktoren Null ist:
 ;
;  Es folgt das Intervall
Es folgt das Intervall ![\(I = [-1;0]\)](https://www.schullv.de/resources/formulas/54151b324b773462e9ba76e5962d8817c1ada11b1c90ec464fdb362cfe5c8690_light.svg) .
2. Schritt: Integral berechnen
Multipliziere den Funktionsterm von
.
2. Schritt: Integral berechnen
Multipliziere den Funktionsterm von  zunächst aus:
zunächst aus:

3.
Diese Aufgabe kannst du in folgenden Schritten berechnen:
 berechnen
2. Schritt:
berechnen
2. Schritt:  berechnen
Setze nun
berechnen
Setze nun  und löse nach
und löse nach  auf:
Durch systematisches Probieren erhält man die Lösung
auf:
Durch systematisches Probieren erhält man die Lösung  , denn:
Die Gleichung kann mögliche weitere Lösungen besitzen. Vereinfache den Funktionsterm zunächst durch Polynomdivision:
Mit der
, denn:
Die Gleichung kann mögliche weitere Lösungen besitzen. Vereinfache den Funktionsterm zunächst durch Polynomdivision:
Mit der  -Formel folgt:
Der Radikand (Ausdruck unter der Wurzel) ist negativ. Somit besitzt die Gleichung keine weiteren Lösungen. Für
-Formel folgt:
Der Radikand (Ausdruck unter der Wurzel) ist negativ. Somit besitzt die Gleichung keine weiteren Lösungen. Für  besitzt die eingeschlossene Fläche den Inhalt
besitzt die eingeschlossene Fläche den Inhalt  .
.
- Berechne den Wert des Integrals in Abhängigkeit von
- Bestimme, für welchen Wert von
das Integral den Wert
annimmt