Ganzrationale Funktionen

Du kannst eine ganzrationale Funktion auf folgende Eigenschaften überprüfen:

Eigenschaft	Methode
Schnittpunkte mit den Koordinatenachsen $(x_0\mid y_0)$	x-Achse: Nullstelle bestimmen, d.h. $y_0 = 0$ , setze also $f(x_0)=0$ und löse nach $x_0$ auf y-Achse: Funktionswert an der Stelle $x_0 = 0$ berechnen, also $y_0 = f(0)$
Extrempunkt $(x_E\mid y_E)$	Notwendiges Kriterium: $f‘(x_E)=0$ Hinreichendes Kriterium: Hochpunkt: $f‘‘(x_E) \lt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $+$ nach $-$ Tiefpunkt: $f‘‘(x_E) \gt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $-$ nach $+$
Wendepunkt $(x_W\mid y_W)$	Notwendiges Kriterium: $f‘‘(x_W)=0$ Hinreichendes Kriterium: $f‘‘‘(x_W) \neq 0$ oder Vorzeichenwechsel von $f‘‘(x)$ in $x_W$
Graph skizzieren	Verwende zum Skizzieren markante Stellen z.B. Nullstellen, Hochpunkte, usw.
Symmetrie	achsensymmetrisch: $f(x)=f(-x)$ punktsymmetrisch: $-f(x)=f(-x)$

Gegeben ist die Funktion $f$ mit $f\left(x\right)=6x^3-9x^2$ . Ihr Schaubild sei $K_f$ .

Bestimme die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

Bestimme die Extrem- und Wendepunkte von $f$ .

Skizziere anhand der bisherigen Ergebnisse den Verlauf von $K_f$ in einem Koordinatensystem.

Prüfe, ob $K_f$ zum Punkt $P\left(0\mid 1\right)$ symmetrisch ist.

Gegeben ist die Gerade $g$ mit $g\left(x\right)=-3x$ .
Bestimme die Schnittpunkte von $K_f$ mit der Geraden $g$ .
An welcher Stelle besitzt $f$ die gleiche Steigung wie die Gerade $g$ ? Berechne die Koordinaten des Berührpunktes der Schaubilder der Funktionen $f$ und $g$ mit $f(x)=5x^2+2x+3$ und $g(x)=5x^3-3x+8$ .

Gegeben ist die Funktion $f$ mit $f\left(x\right)=\dfrac{1}{2}x^3-2x^2-2x+8$ . Ihr Schaubild sei $K_f$ .

Bestimme die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

Bestimme die Extrema und Wendepunkte von $K_f$ .

Skizziere anhand der bisherigen Ergebnisse den Verlauf von $K_f$ in einem Koordinatensystem.

Prüfe, ob $K_f$ zur $y$ -Achse symmetrisch ist.

Bestimme die Gleichung der Tangente, die das Schaubild von $f$ im Schnittpunkt mit der $y$ -Achse berührt.

Gegeben ist die Funktion $f_k$ mit $f_k\left(x\right)=\dfrac{1}{2}x^2-3kx$ . Ihr Schaubild sei $K_f$ .

Bestimme die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

Bestimme die Extrema und Wendepunkte von $K_f$ . Geben Sie die Ortskurve der Tiefpunkte an.

Skizziere anhand der bisherigen Ergebnisse den Verlauf von $K_f$ für $k=1$ in einem Koordinatensystem.

Beweise, dass $K_f$ achsensymmetrisch zur Geraden mit der Gleichung $x=3k$ ist.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Gegeben ist die Funktion $f$ mit $f\left(x\right)=6x^3-9x^2$ .

Schnittpunkte von $K_f$ mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f\left(x\right)=0$ setzen und nach $x$ auflösen

$\begin{array}{rll} 6x^3-9x^2&=&0&\scriptsize{\mid\;:6}\\[5pt] x^3-\dfrac{3}{2}x^2&=&0&\scriptsize{ x^2\; \text{ausklammern}}\\[5pt] x^2\left(x-\dfrac{3}{2}\right)&=&0\\[5pt] \end{array}$

Nach dem Satz von Nullprodukt ist ein Produkt gleich Null, wenn einer seiner Faktoren Null ist:

$x_{1,2}=0$

oder

$\begin{array}{rll} x-\dfrac{3}{2}&=&0&\scriptsize{\mid\;+\dfrac{3}{2}}\\[5pt] x_3&=&\dfrac{3}{2}\\[5pt] \end{array}$

Daraus ergeben sich die Punkte $N_{1,2}\left(0\mid\;0\right)$ und $N_3\left(\dfrac{3}{2}\mid\;0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse: $x=0$ setzen und ausrechnen

$\begin{array}{rll} 6\cdot0^3-9\cdot0^2&=&f\left(0\right)\\[5pt] 0&=&f\left(0\right)\\[5pt] \end{array}$

Daraus ergibt sich der Punkt $P\left(0\mid\;0\right)$ .

Extrem- und Wendepunkte von $K_f$ bestimmen

$\begin{array}{rll} f\left(x\right)&=&6x^3-9x^2\\[5pt] f‘\left(x\right)&=&18x^2-18x\\[5pt] f‘‘\left(x\right)&=&36x-18\\[5pt] f‘‘‘\left(x\right)&=&36 \end{array}$

$\blacktriangleright$ Extrempunkte bestimmen: $f‘(x)=0$ setzen:

$\begin{array}{rll} 18x^2-18x&=&0&\scriptsize{\mid\;:18}\\[5pt] x^2-x&=&0&\scriptsize{x\;\text{ ausklammern}}\\[5pt] x\left(x-1\right)&=&0 \end{array}$

Nach dem Satz von Nullprodukt ist ein Produkt gleich Null, wenn einer seiner Faktoren Null ist.

$x_1=0$

$\begin{array}{rll} x-1&=&0&\scriptsize{\mid\;+1}\\ x_2&=&1 \end{array}$

Hochpunkt oder Tiefpunkt? $x_1=0$ und $x_2=1$ in $f‘‘(x)$ einsetzen:

$\begin{array}{rll} f‘‘\left(0\right)&=&36\cdot0-18&< 0 \rightarrow \text{Hochpunkt}\\[5pt] f‘‘\left(1\right)&=&36\cdot1-18& > 0 \rightarrow \text{Tiefpunkt} \end{array}$

Setze nun die Werte $x_1=0$ und $x_2=1$ in die Funktionsgleichung von $f$ ein, um jeweils die vollständigen Koordinaten zu bestimmen.

$x_1=0$ :

$\begin{array}{rll} f\left(x\right)&=&6x^3-9x^2\\[5pt] f\left(0\right)&=&6\cdot0^3-9\cdot0^2\\[5pt] f\left(0\right)&=&0 \end{array}$

$x_2=1$ :

$\begin{array}{rll} f\left(x\right)&=&6x^3-9x^2\\[5pt] f\left(1\right)&=&6\cdot1^3-9\cdot1^2\\[5pt] f\left(1\right)&=&-3 \end{array}$

Der Hochpunkt hat die Koordinaten $H(0\mid\;0)$ und der Tiefpunkt hat die Koordinaten $T(1\mid\;-3)$ .

$\blacktriangleright$ Wendepunkt bestimmen: $f‘‘(x)=0$ setzen:

$\begin{array}{rll} 36x-18&=&0&\scriptsize{\mid\;+18}\\[5pt] 36x&=&18&\scriptsize{\mid\;:36}\\[5pt] x&=&\dfrac{1}{2} \end{array}$

Echter Wendepunkt?
$x=\dfrac{1}{2}$ in $f‘‘‘(x)$ einsetzen:

$\begin{array}{rll} f‘‘‘\left(\dfrac{1}{2}\right)&=&36&\neq 0 \rightarrow \text{echter Wendepunkt} \end{array}$

Setze nun den Wert $x=\dfrac{1}{2}$ in $f$ ein.

$\begin{array}{rll} f\left(x\right)&=&6x^3-\; ... \end{array}$

Vollständige Lösung anzeigen

Der Wendepunkt hat die Koordinaten $W\left(\dfrac{1}{2}\mid\;-\dfrac{3}{2}\right)$ .

Anhand der bisherigen Ergebnisse den Verlauf von $K_f$ in einem Koordinatensystem skizzieren

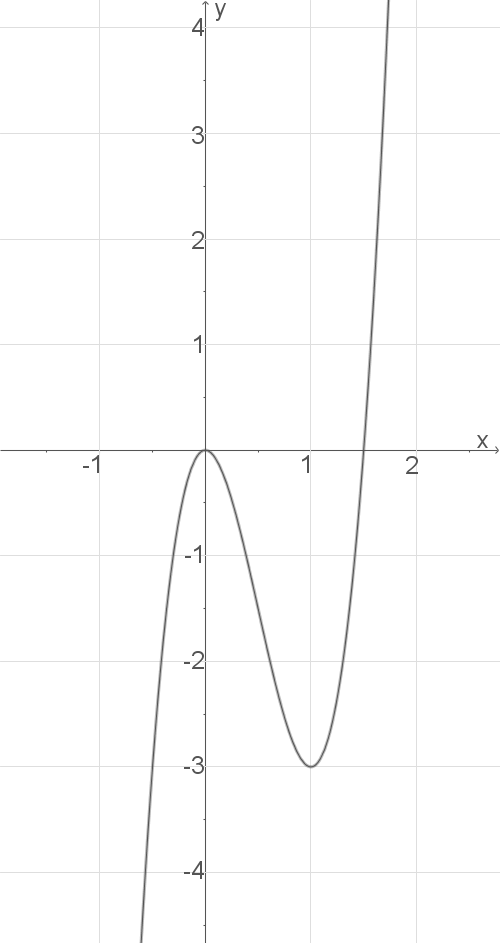
Graf einer mathematischen Funktion mit x- und y-Achse in einem kartesischen Koordinatensystem.

Prüfen, ob $K_f$ zum Punkt $P\left(0\mid\;1\right)$ symmetrisch ist

Behauptung: $K_f$ ist punktsymmetrisch zu $P\left(0\mid\;1\right)$

Zu zeigen:

$\begin{array}{rll} f\left(x+h\right)+f\left(x-h\right)&=&2y&\\\rightarrow\scriptsize{P(0|1)\;\text{einsetzen}}\\ \Rightarrow\left(h\right)+f\left(-h\right)&=&2\cdot1\\ \end{array}$

Beweis:

$\begin{array}{rll} 6\cdot h^3-9h^2+ ... \end{array}$

Vollständige Lösung anzeigen

Dies ist eine falsche Aussage. $h^2$ ergibt immer eine positive Zahl, deshalb ergibt $-18h^2$ immer eine negative Zahl. $-18h^2$ kann also niemals 2 ergeben! Daher ist $K_f$ nicht symmetrisch zum Punkt $P(0|1)$ .

Schnittpunkte von $K_f$ mit der Geraden $g$ bestimmen

$\begin{array}{rll} 6x^3-9x^2&=\;... \end{array}$

Vollständige Lösung anzeigen

Nach dem Satz vom Nullprodukt ist ein Produkt gleich Null, wenn einer seiner Faktoren Null ist:

$x_1=0$

$\begin{array}{rll} 6x^2-9x+3&=&0&\scriptsize{\mid\;:6}\\[5pt] x^2-\dfrac{3}{2}x+\dfrac{1}{2}&=&0 \end{array}$

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} x_{2,3}&=&\dfrac{3}{4}\pm\sqrt{\dfrac{9}{16}-\dfrac{1}{2}}\\[5pt] &=&\dfrac{3}{4}\pm\sqrt{\dfrac{1}{16}}\\[5pt] &=&\dfrac{3}{4}\pm\dfrac{1}{4}\\[5pt] x_2&=&\dfrac{1}{2}\\[5pt] x_3&=&1 \end{array}$

$y$ -Koordinaten der Schnittpunkte bestimmen:

$\begin{array}{rll} g\left(0\right)&=&0\\[5pt] g\left(\dfrac{1}{2}\right)&=&-\dfrac{3}{2}\\[5pt] g\left(1\right)&=&-3 \end{array}$

Daraus ergeben sich die drei Punkte $S_1\left(0\mid\;0\right)$ , $S_2\left(\dfrac{1}{2}\mid\;-\dfrac{3}{2}\right)$ und $S_3\left(1\mid\;-3\right)$ .

$\blacktriangleright$ Stelle von $f$ mit gleicher Steigung suchen

$f‘\left(x\right)=-3$ setzen und ausrechnen:

$\begin{array}{rll} 18x^2-18x&=&-3&\scriptsize{\mid\;+3}\\[5pt] 18x^2-18x+3&=&0&\scriptsize{\mid\;:18}\\[5pt] x^2-x+\dfrac{1}{6}&=&0 \end{array}$

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} x_{1,2}&=&\dfrac{1}{2}\pm\sqrt{\dfrac{1}{4}-\dfrac{1}{6}}\\[5pt] &=&\dfrac{1}{2}\pm\sqrt{\dfrac{1}{12}}\\[5pt] x_1&\approx&0,21\\[5pt] x_2&\approx&0,79 \end{array}$

An den Stellen $x=0,21$ und $x=0,79$ besitzt $K_f$ die Steigung $-3.$

$\blacktriangleright$ Berührpunkte bestimmen

Die Graphen von $f$ und $g$ berühren sich in den Punkten, in denen sie sowohl den gleichen Funktionswert, als auch die gleiche Steigung besitzen.

Für die 1. Ableitungsfunktion gilt jeweils:

$\begin{array}[t]{rll} f‘(x)&=& 10x+2 \\[5pt] g‘(x)&=& 15x^2-3 \end{array}$

Gleichsetzen liefert die Stellen, an denen beide Graphen die gleiche Steigung haben:

$\begin{array}[t]{rll} f‘(x)&=&g‘(x) \\[5pt] x_1&=& \frac{1}{3}- \frac{2}{3} \\[5pt] &=& -\frac{1}{3}\\[10pt] x_2&=& \frac{1}{3}+ \frac{2}{3} \\[5pt] &=& \frac{1}{3} + \frac{2}{3} \\[5pt] &=& 1 \end{array}$

Vollständige Lösung anzeigen

Überprüfe nun die Funktionswerte an diesen Stellen:

$\begin{array}[t]{rll} f\left(-\frac{1}{3}\right)&=& \frac{26}{9} \\[10pt] g\left(-\frac{1}{3}\right)&=& \frac{238}{27}\\[10pt] f(1)&=& 10 \\[10pt] g(1)&=& 10 \end{array}$

Vollständige Lösung anzeigen

Die Graphen von $f$ und $g$ berühren sich im Punkt $P(1\mid 10).$

Gegeben ist die Funktion $f$ mit $f\left(x\right)=\dfrac{1}{2}x^3-2x^2-2x+8$ .

Schnittpunkte von $K_f$ mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f\left(x\right)=0$ setzen und nach $x$ auflösen

$\begin{array}{rll} \dfrac{1}{2}x^3-2x^2-2x+8&=&0&\scriptsize{\mid\;\cdot2}\\[5pt] x^3-4x^2-4x+16&=&0\\ \end{array}$

Nullstelle erraten: $x_1=4$

$\begin{array}{rll} f\left(4\right)&=&4^3-4\cdot4^2-\;... \end{array}$

Vollständige Lösung anzeigen

Polynomdivision:

$\begin{array}{rll} (x^3-4x^2-4x+16):\;... \end{array}$

Vollständige Lösung anzeigen

$\begin{array}{rll} x^2-4&=&0&\scriptsize{\mid\;+4}\\[5pt] x^2&=&4&\scriptsize{\mid\;\sqrt{\;}}\\[5pt] x_{2,3}&=&\pm2 \end{array}$

Daraus ergeben sich die Punkte $N_1\left(4\mid\;0\right)$ , $N_2\left(-2\mid\;0\right)$ und $N_3\left(2\mid\;0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:
$x=0$ setzen und ausrechnen:

$\begin{array}{rll} \dfrac{1}{2}\cdot0^3-2\cdot0^2-\;... \end{array}$

Vollständige Lösung anzeigen

Daraus ergibt sich der Punkt $P\left(0\mid\;8\right)$ .

Extrema und Wendepunkte von $K_f$ bestimmen

$\begin{array}{rll} f\left(x\right)&=&\dfrac{1}{2}x^3-2x^2-2x+8\\[5pt] f‘\left(x\right)&=&\dfrac{3}{2}x^2-4x-2\\[5pt] f‘‘\left(x\right)&=&3x-4\\[5pt] f‘‘‘\left(x\right)&=&3 \end{array}$

$\blacktriangleright$ Extrema bestimmen: $f‘(x)=0$ setzen

$\begin{array}{rll} \dfrac{3}{2}x^2-4x-2&=&0&\scriptsize{\mid\;\cdot\dfrac{2}{3}}\\[5pt] x^2-\dfrac{8}{3}x-\dfrac{4}{3}&=&0\\[5pt] \end{array}$

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} x_{1,2}&=&\dfrac{8}{6}\pm\sqrt{\dfrac{64}{36}+\dfrac{4}{3}}\\[5pt] &=&\dfrac{4}{3}\pm\sqrt{\dfrac{28}{9}}\\[5pt] x_1&\approx&-0,43\\[5pt] x_2&\approx&3,1\\[5pt] \end{array}$

Hochpunkt oder Tiefpunkt? $x_1=-0,43$ und $x_2=3,1$ in $f‘‘(x)$ einsetzen:

$\begin{array}{rll} f‘‘\left(-0,43\right)&=&3\cdot\left(-0,43\right)-4&\\\scriptsize{ < 0: \text{Hochpunkt}}\\[5pt] f‘‘\left(3,1\right)&=&3\cdot3,1-4&\\\scriptsize{ > 0: \text{Tiefpunkt}} \end{array}$

Setze nun die Wert von $x$ in die Funktionsgleichung von $f$ ein, um die vollständigen Koordinaten zu bestimmen.

$x_1=-0,43$ :

$\begin{array}{rll} f\left(x\right)&=&\dfrac{1}{2}x^3-\;... \end{array}$

Vollständige Lösung anzeigen

$x_2=3,1$ :

$\begin{array}{rll} f\left(x\right)&=&\dfrac{1}{2}x^3-\;... \end{array}$

Vollständige Lösung anzeigen

Der Hochpunkt hat die Koordinaten $H(-0,43\mid\;8,5)$ . Der Tiefpunkt hat die Koordinaten $T(3,1\mid\;-2,5)$ .

$\blacktriangleright$ Wendepunkt bestimmen:
$f‘‘(x)=0$ setzen

$\begin{array}{rll} 3x-4&=&0&\scriptsize{\mid\;+4}\\[5pt] 3x&=&4&\scriptsize{\mid\;:3}\\[5pt] x&=&\dfrac{4}{3} \end{array}$

Echter Wendepunkt?
$x=\dfrac{4}{3}$ in $f‘‘‘(x)$ einsetzen:

$\begin{array}{rll} f‘‘‘\left(\frac{4}{3}\right)&=3&\scriptsize{\neq0\;\;\\\Rightarrow\;\;\text{Wendepunkt}} \end{array}$

Setze nun $x=\dfrac{4}{3}$ in die Funktionsgleichung von $f$ ein.

$\begin{array}{rll} f\left(x\right)&=&\dfrac{1}{2}x^3-\;... \end{array}$

Vollständige Lösung anzeigen

Der Wendepunkt hat die Koordinaten $W\left(\dfrac{4}{3}\mid\;2,96\right)$ .

Anhand der bisherigen Ergebnisse den Verlauf von $K_f$ in einem Koordinatensystem skizzieren

Graph einer Funktion mit x- und y-Achse, zeigt Kurvenverlauf in einem Koordinatensystem.

Prüfen, ob $K_f$ zur $y$ -Achse symmetrisch ist

Behauptung: $K_f$ ist achsensymmetrisch zu $x=0$

Zu zeigen:

$\begin{array}{rll} f\left(x\right)&=&f\left(-x\right) \end{array}$

Beweis:

$\begin{array}{rll} \dfrac{1}{2}x^3-2x^2-2x+8=\;... \end{array}$

Vollständige Lösung anzeigen

Dies ist eine falsche Aussage. Die Achsensymmetrie zur $y$ -Achse ist also widerlegt.

Gleichung der Tangente bestimmen, die das Schaubild von $f$ im Schnittpunkt mit der $y$ -Achse berührt

Schnittpunkt mit der $y$ -Achse: $P\left(0\mid\;8\right)$

Steigung im Schnittpunkt bestimmen: $f‘(0)$ berechnen:

$\begin{array}{rll} f‘\left(0\right)&=&\dfrac{3}{2}\cdot0^2-4\cdot0-2\\[5pt] &=&-2 \end{array}$

Allgemeine Tangentengleichung anwenden:

Setze die Koordinaten von $P$ für $u$ und $f(u)$ und die eben berechnete Steigung für $f‘(u)$ ein:

$\begin{array}{rll} t:y&=&f‘\left(u\right)\cdot\left(x-u\right)+f\left(u\right)\\[5pt] &=&-2\left(x+0\right)+8\\[5pt] &=&-2x+8\\[5pt] t:y&=&-2x+8 \end{array}$

Die Tangentengleichung lautet: $t:y=-2x+8$

Gegeben ist die Funktion $f_k$ mit $f_k\left(x\right)=\dfrac{1}{2}x^2-3kx$ .

Schnittpunkte von $K_f$ mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f_k\left(x\right)=0$ setzen und nach $x$ auflösen

$\begin{array}{rll} \dfrac{1}{2}x^2-3kx&=&0&\scriptsize{\mid\;\cdot2}\\[5pt] x^2-6kx&=&0&\scriptsize{\mid\;x}\\[5pt] x\left(x-6k\right)&=&0 \end{array}$

Nach dem Satz vom Nullprodukt ist ein Produkt gleich 0, wenn einer seiner Faktoren 0 ist:

$\begin{array}{rll} x_1&=&0\\[5pt] x_2&=&6k \end{array}$

Daraus ergeben sich die Punkte $N_1\left(0\mid\;0\right)$ und $N_2\left(6k\mid\;0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:
$x=0$ setzen und ausrechnen

$\begin{array}{rll} \dfrac{1}{2}\cdot0^2-3k\cdot0&=&f\left(0\right)\\[5pt] 0&=&f\left(0\right) \end{array}$

Daraus ergibt sich der Punkt
$P\left(0\mid\;0\right)$ .

Extrema und Wendepunkte von $K_f$ bestimmen und Ortskurve der Tiefpunkte angeben

$\begin{array}{rll} f_k\left(x\right)&=&\dfrac{1}{2}x^2-3kx\\[5pt] f_k‘\left(x\right)&=&x-3k\\[5pt] f_k‘‘\left(x\right)&=&1 \end{array}$

$\blacktriangleright$ Extrema bestimmen: $f_k‘(x)=0$ setzen

$\begin{array}{rll} x-3k&=&0&\scriptsize{\mid\;+3k}\\[5pt] x&=&3k \end{array}$

Hochpunkt oder Tiefpunkt? $x=3k$ in $f_k‘‘(x)$ einsetzen:

$\begin{array}{rll} f_k‘‘\left(3k\right)&=&1&\scriptsize{>0: \text{Tiefpunkt}} \end{array}$

Setze den Wert $x=3k$ in die Funktionsgleichung von $f_k$ ein, um die vollständigen Koordinaten des Tiefpunktes $T$ zu erhalten.

$\begin{array}{rll} f_k\left(x\right)&=&\dfrac{1}{2}x^2-3kx\\[5pt] f_k\left(3k\right)&=&\dfrac{1}{2}\cdot(3k)^2-3k\cdot 3k\\[5pt] f_k\left(3k\right)&=&\dfrac{1}{2}\cdot9k^2-9k^2\\[5pt] f_k\left(3k\right)&=&-\dfrac{9}{2}k^2 \end{array}$

Der Tiefpunkt hat die Koordinaten $T\left(3k\mid\;-\dfrac{9}{2}k^2\right)$ .

$\blacktriangleright$ Wendepunkt bestimmen: $f_k‘‘(x)=0$ setzen

$\begin{array}{rll} 1&=&0 \end{array}$

Dies ist eine falsche Aussage. $f_k‘‘(x)$ kann nicht 0 werden, es gibt also auch keinen Wendepunkt.

$\blacktriangleright$ Ortskurve der Tiefpunkte bestimmen

$y$ -Koordinate des Tiefpunktes bestimmen:

$\begin{array}{rll} f_k\left(3k\right)&=&\dfrac{1}{2}\cdot\left(3k\right)^2-3k\cdot3k\\[5pt] &=&\dfrac{1}{2}\cdot9k^2-9k^2\\[5pt] f_k\left(3k\right)&=&-\dfrac{1}{2}\cdot9k^2 \end{array}$

Tiefpunkt aufteilen:

$\begin{array}{rll} x&=&3k\\[5pt] y&=&-\dfrac{1}{2}\cdot9k^2\\ \end{array}$

$x$ -Koordinate nach $k$ auflösen:

$\begin{array}{rll} x&=&3k&\scriptsize{\mid\;:3}\\[5pt] \dfrac{1}{3}x&=&k \end{array}$

$k$ einsetzen in $y$ -Koordinate:

$\begin{array}{rll} y&=&-\dfrac{1}{2}\cdot9\left(\dfrac{1}{3}x\right)^2\\[5pt] y&=&-\dfrac{1}{2}\cdot9\cdot\dfrac{1}{9}x^2\\[5pt] y&=&-\dfrac{1}{2}x^2 \end{array}$

Daraus folgt die Gleichung der Ortskurve:
$y=-\dfrac{1}{2}x^2$

Anhand der bisherigen Ergebnisse Verlauf von $K_f$ für $k=1$ in Koordinatensystem skizzieren

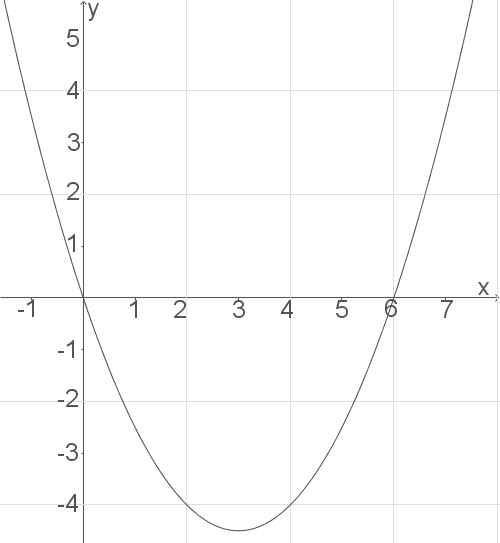
Graf einer Parabel mit x- und y-Achse, dargestellt auf schwarzem Hintergrund.

Beweisen, dass $K_f$ achsensymmetrisch zu $x=3k$ ist

Behauptung: $K_f$ ist achsensymmetrisch zu $x=3k$

Zu zeigen:

$\begin{array}{rll} f_k\left(x+h\right)&=&f_k\left(x-h\right)\\[5pt] f_k\left(3k+h\right)&=&f_k\left(3k-h\right) \end{array}$

Beweis:

$\begin{array}{rll} \dfrac{1}{2}\left(3k+h\right)^2-\;... \end{array}$

Vollständige Lösung anzeigen

Dies ist eine wahre Aussage. Die Achsensymmetrie zu $x=3k$ ist also bewiesen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?