Vermischte Aufgaben

Gegeben sind die Punkte $A(-3\mid-2\mid1)$ , $B(-1\mid0\mid5)$ und $C(6\mid0\mid-1)$ .

Liegen diese drei Punkte in einer

Geraden?

Welcher Punkt $D$ auf der Geraden durch

$A$ und $C$ ist von $A$ und $B$ gleich weit entfernt?

Gegeben sind die Punkte $A(-5\mid-2\mid1)$ , $B(0\mid3\mid-5)$ und $C(2\mid1\mid-4)$ .

Die Punkte $A$ , $B$ und $C$ liegen in der Ebene $E$ . Gib eine Koordinatengleichung von $E$ an.

Bestimme den Abstand von $E$ zum Ursprung.

Gegeben sind die Ebene $E$ und der Punkt $T$ :

$E:\;$ $\left[ {\overrightarrow{x} - \left( {\begin{array}{*{20}r} 3 \\ 4 \\ { - 6} \\ \end{array}} \right)} \right] \cdot \left( {\begin{array}{*{20}r} 2 \\ 3 \\ { - 1} \\ \end{array}} \right) = 0$

$\hspace{1cm} T(1 \mid -5 \mid -9)$

Berechne den Abstand des Punktes $T$

zur Ebene $E$ .

Die Geraden $g:\overrightarrow{x}=\left(\begin{array}{r} 2\\ 0\\ -1\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 2\\ 4\\ 3\\ \end{array}\right)$ und $h:\overrightarrow{x}=\left(\begin{array}{r} 6\\ 2\\ -7\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 0\\ 2\\ 4\\ \end{array}\right)$ schneiden sich in einem Punkt $S$ .

Berechne den Abstand von $S$ zur Ebene $E:2x_1+x_3=4$ .

Welcher Punkt auf $g:\overrightarrow{x}=\left(\begin{array}{r} -2\\ 14\\ 7\\ \end{array}\right)+t\cdot\left(\begin{array}{r} -1\\ 2\\ 1\\ \end{array}\right)$ hat den Abstand $4$ LE von

$E:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 1\\ 0\\ \end{array}\right)+r\cdot\left(\begin{array}{r} -2\\ 0\\ 1\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 2\\ -2\\ 1\\ \end{array}\right)$ ?

Gegeben ist eine Gerade $g:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 1\\ 2\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 3\\ 0\\ -1\\ \end{array}\right)$ .

Zeige, dass der Punkt $A\left(10 \mid 1 \mid -1\right)$ auf $g$ liegt.

Eine weitere Gerade verläuft durch die Punkte $P\left(9 \mid -2 \mid 4\right)$ und $Q\left(14 \mid 8 \mid -1\right)$ .

Bestimme den Abstand von $A$ zu

dieser Geraden.

Gegeben ist eine Ebene $E:2x_1+2x_2-x_3=4$ , sowie ein Punkt $P\left(k \mid 5 \mid k\right)$ .

Bestimme $k$ so, dass $P$ genau 3 LE von

$E$ entfernt ist.

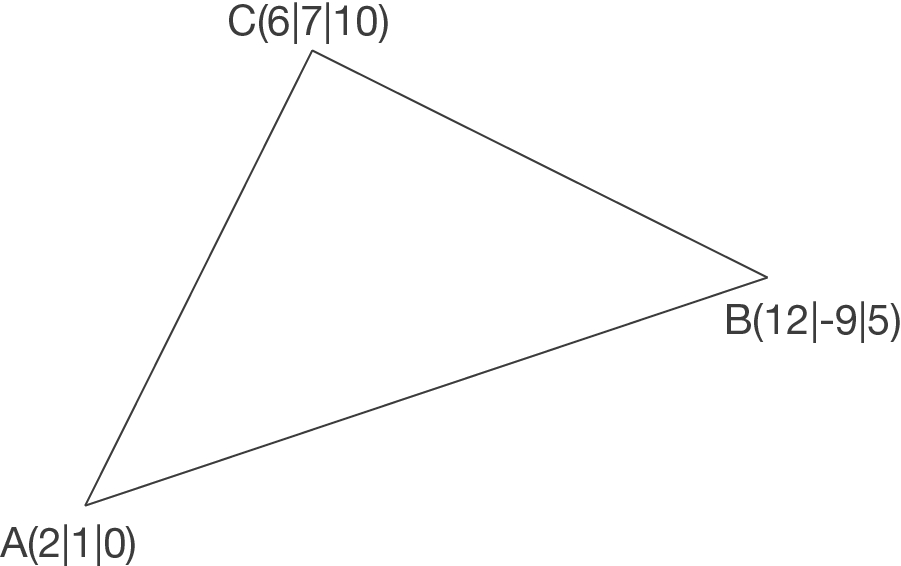
Bestimme den Inhalt des Dreiecks $ABC$ :

Dreieck mit den Punkten A, B und C im dreidimensionalen Raum, dargestellt durch Koordinaten.

Berechne den Inhalt des Parallelogramms:

Diagramm eines Rechtecks mit den Punkten A, B, C und D sowie ihren Koordinaten.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Gegeben sind die Punkte $A(-3 \mid -2 \mid 1)$ , $B(-1 \mid 0 \mid 5)$ und $C(6 \mid 0 \mid -1)$ .

$\blacktriangleright$ Untersuchen ob $A$ , $B$ , $C$ in einer Geraden liegen

1. Schritt: Aufstellen einer Geradengleichung $g$ durch $A$ und $C$

$g:\;\overrightarrow{x}=\overrightarrow{A}+s\cdot\overrightarrow{AC}$

Vollständige Lösung anzeigen

2. Schritt: Überprüfen ob $B$ auf $g$ liegt $\Rightarrow\overrightarrow{x}=B$

$g:\;\left(\begin{array}{r} -1\\ 0\\ 5\\ \end{array}\right)=\left(\begin{array}{r} -3\\ -2\\ 1\\ \end{array}\right)+s\left(\begin{array}{r} 9\\ 2\\ -2\\ \end{array}\right)$

$\begin{array}{rrll} -1=&-3&+&9s&\quad\Rightarrow\;s=\dfrac{2}{9}\\[5pt] 0=&-2&+&2s&\quad\Rightarrow\;s=1\\[5pt] 5=&1&-&2s&\quad\Rightarrow\;s=-2\\[5pt] \end{array}$

Es gibt kein $s$ , sodass alle drei Gleichungen erfüllt sind. $B$ liegt somit nicht auf $g$ und damit liegen die drei Punkte $A$ , $B$ und $C$ auch nicht in einer Geraden.

Skizze:

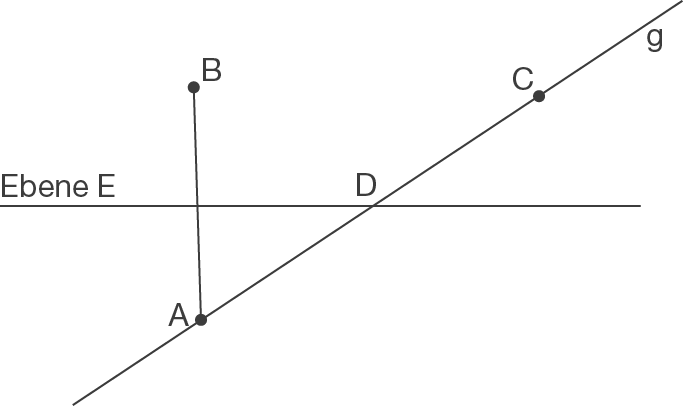
Diagramm mit einer Ebene E, Punkten A, B, C und einer Linie g.

$\blacktriangleright$ Bestimmung des Punktes $D$

Alle Punkte, die von $A$ und $B$ gleich weit entfernt sind, liegen in der Ebene $E$ , die orthogonal zur Geraden durch $A$ und $B$ verläuft und durch den Mittelpunkt von $\overline{AB}$ verläuft.

Der Vektor $\overrightarrow{AB}$ ist ein Normalenvektor von $E$ .

1. Schritt: Bestimmung des Mittelpunktes $M$ von $\overline{AB}$

$\Rightarrow\;M(-2 \mid -1 \mid 3)$

Vollständige Lösung anzeigen

2. Schritt: Aufstellen einer Ebene von $E$

$\overrightarrow{AB}=\left(\begin{array}{r} 2\\ 2\\ 4\\ \end{array}\right)$ $\Rightarrow\;\overrightarrow{n_E}$ = $\left(\begin{array}{r} 2\\ 2\\ 4\\ \end{array}\right)$ $\Rightarrow\;E$ : $2x+2y+4z=d$

$M(-2 \mid -1 \mid 3)$ eingesetzt in $E$ :

$d=2x+2y+4z$ = $2 \cdot (-2) + 2 \cdot (-1) + 4 \cdot 3$ = $-4-2+12=6$

$\Rightarrow\;E$ : $2x+2y+4z$ = $6$

Der Punkt $D$ befindet sich auf der Geraden durch $A$ und $C$ , also auf der Geraden $g$ . $D$ ist der Schnittpunkt von $g$ und $E$ .

3. Schritt: Bestimmung des Schnittpunkts $D$ von $g$ und $E$ ( $g$ eingesetzt in $E$ )

$2(-3+9s)+2(-2+2s)+4(1-2s)$ = $6$ $\Rightarrow\; s=\dfrac{6}{7}$

$s=\dfrac{6}{7}$ eingesetzt in $g$ liefert den Punkt $D\left(\frac{33}{7} \mid -\frac{2}{7} \mid -\frac{5}{7}\right)$ .

Gegeben $A(-5 \mid -2 \mid 1)$ , $B(0 \mid 3 \mid -5)$ und $C(2 \mid 1 \mid -4)$ .

Bestimmung einer Koordinatengleichung von $E$

$E:\;\overrightarrow{x}=\overrightarrow{OA}+r\cdot\overrightarrow{AB}+s\cdot\overrightarrow{AC}$

$E:\;\overrightarrow{x}=$

Vollständige Lösung anzeigen

Mit dem Kreuzprodukt berechnet man einen Normalenvektor von $E$ :

$\left(\begin{array}{r} 5\\ 5\\ -6\\ \end{array}\right)\times\left(\begin{array}{r} 7\\ 3\\ -5\\ \end{array}\right)=\left(\begin{array}{r} -7\\ -17\\ -20\\ \end{array}\right)=$ $\overrightarrow{n}:(-1)=\begin{pmatrix}7\\17\\20\end{pmatrix}$

$\Rightarrow\;E:\;7x+17y+20z=d$

$A$ eingesetzt in $E$ liefert:

$E:\;7x+17y+20z=-49$

Bestimmung des Abstandes von
$E$ zum Ursprung

HNF von $E$ : $\dfrac{\left|7x+17y+20z+49\right|}{\sqrt{7^2+17^2+20^2}}$ = $0$

$d(0;E)\approx1,80$

Vollständige Lösung anzeigen

Um den Abstand des Punktes $T(1 \mid -5 \mid -9)$ zur Ebene $E$ zu bestimmen benötigt man die HNF von $E$ .

Bestimmung einer Koordinatenform
von $E$

$E:\;2x+3y-z=d$ mit dem Punkt $(3 \mid 4 \mid -6)$ eingesetzt ergibt sich:

$E:\;2\cdot3+3\cdot4-(-6)=d=24$ $\Rightarrow\;E:\; 2x+3y-z=24$

HNF von $E$ : $\dfrac{\left|2x+3y-z-24\right|}{\sqrt{2^2+3^2+(-1)^2}}=0$ .

$T$ eingesetzt liefert:

$\dfrac{\left|2\cdot1+3\cdot(-5)-(-9)-24\right|}{\sqrt{14}}=$ $\dfrac{\left|-28\right|}{\sqrt{14}}\approx7,5$

Der Punkt $T$ ist somit $7,5$ LE von $E$ entfernt.

1. Schritt: Schnittpunkt der Geraden berechnen

Wir setzen die Geradengleichungen

gleich:

$\left(\begin{array}{r} 2\\ 0\\ -1\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 2\\ 4\\ 3\\ \end{array}\right)$ = $\left(\begin{array}{r} 6\\ 2\\ -7\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 0\\ 2\\ 4\\ \end{array}\right)$ .

Daraus ergibt sich ein lineares Gleichungssystem:

$\begin{array}{lrlll} Ⅰ&2&+&2r&=&6 \end{array}$

Vollständige Lösung anzeigen

Wird $s=3$ eingesetzt in $h$ , so ergibt sich der Punkt $S\left(6 \mid 8 \mid 5\right)$ .

2. Schritt: Hessesche Normalenform
von $E$ bestimmen

Wir bringen die Gleichung auf die Form $d=\dfrac{\left|ax_1+bx_2+cx_3-d\right|}{\left|\overrightarrow{n}\right|}$ .

$d=\dfrac{\left|2x_1+x_3-4\right|}{\sqrt{2^2+1^2}}=\dfrac{\left|2x_1+x_3-4\right|}{\sqrt5}$

Wir setzen die Koordinaten von $S$ in die Gleichung ein und bestimmen somit den Abstand von $S$ zu $E$ .

$d=\dfrac{\left|2\cdot6+5-4\right|}{\sqrt5}=\dfrac{13}{\sqrt5}\approx5,81$

1. Schritt: Punkt auf $g$ bestimmen

Jeder Punkt $Q$ auf $g$ hat die Koordinaten $Q\left(-2-t \mid 14+2t \mid 7+t\right)$ .

Wir bestimmen nun den Abstand von $Q$

zu $E$ . Dazu bilden wir die Hessesche Normalenform von $E$ .

2. Schritt: Normalenform von
$E$ bestimmen

Den Normalenvektor von $E$ bestimmen

wir über das Kreuzprodukt

der Spannvektoren.

$\overrightarrow{n}=\left(\begin{array}{c} -2\\ 0\\ 1\\ \end{array}\right)\times\left(\begin{array}{c} 2\\ -2\\ 1\\ \end{array}\right)=$

Vollständige Lösung anzeigen

Die Normalenform von $E$ lautet also $E:\left[\overrightarrow{x}-\left(\begin{array}{r} 1\\ 1\\ 0\\ \end{array}\right)\right]\circ\left(\begin{array}{r} 2\\ 4\\ 4\\ \end{array}\right)=0$ .

Um die Hessesche Normalenform zu erhalten, bringen wir die Gleichung auf die Form $d=\left|\left[\overrightarrow{x}-\overrightarrow{p}\right]\circ\dfrac{\overrightarrow{n}}{\left|\overrightarrow{n}\right|}\right|$ .

$d=$

Vollständige Lösung anzeigen

Wir setzen die Koordinaten von

$Q$ für $x$ ein. Der Abstand soll $d=4$ betragen:

$\ 4=$

Vollständige Lösung anzeigen

Daraus ergeben sich die Punkte $Q_1\left(3 \mid 4 \mid 2\right)$ und $Q_2\left(7,8\mid-5,6\mid-2,8\right)$ .

Gegeben ist eine Gerade $g:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 1\\ 2\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 3\\ 0\\ -1\\ \end{array}\right)$ .

Nachweisen, dass $A$ auf $g$ liegt: $A$ in $g$ einsetzen

$\left(\begin{array}{r} 10\\ 1\\ -1\\ \end{array}\right)=\left(\begin{array}{r} 1\\ 1\\ 2\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 3\\ 0\\ -1\\ \end{array}\right)$

Daraus ergibt sich ein lineares Gleichungssystem:

$\begin{array}{lrlll} Ⅰ&10&=&1&+&3r& \end{array}$

Vollständige Lösung anzeigen

Für $r=3$ liegt $A$ auf $g$ .

Geradengleichung aufstellen

$\begin{array}{rll} h:\overrightarrow{x}=&\overrightarrow{P}+s\cdot\overrightarrow{PQ}\\[5pt] =&\left(\begin{array}{r} 9\\ -2\\ 4\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 5\\ 10\\ -5\\ \end{array}\right) \end{array}$

Jeder Punkt $T$ auf der Geraden $h$

hat die Koordinaten $T\left(9+5s \mid -2+10s \mid 4-5s\right)$ .

Wir bestimmen zunächst den Verbindungsvektor von $A$ und $T$ :

$\overrightarrow{AT}=$

Vollständige Lösung anzeigen

Dieser Verbindungsvektor soll

senkrecht zur Geradenstehen, sein Skalarprodukt mit dem Richtungsvektor der Geraden soll also Null ergeben:

$\begin{array}{rll} 0=&\left(\begin{array}{r} -1+5s\\ -3+10s\\ 5-5s\\ \end{array}\right)\cdot\left(\begin{array}{r} 5\\ 10\\ -5\\ \end{array}\right)\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Für $s=0,4$ erhalten wir also den

Punkt $T$ auf $h$ , der den kleinsten Abstand zu $A$ hat. Der Betrag des Verbindungsvektors von $T$ und $A$ gibt uns dann den Abstand des Punktes zur Geraden an.

$\left|\overrightarrow{AT}\right|=$

Vollständige Lösung anzeigen

Hessesche Normalenform
von $E$ bestimmen

Wir bringen die Gleichung auf die Form $d=\dfrac{\left|ax_1+bx_2+cx_3-d\right|}{\left|\overrightarrow{n}\right|}$ .

$d=\dfrac{\left|2x_1+2x_2-x_3-4\right|}{\sqrt{4+4+1}}$ $=\dfrac{\left|2x_1+2x_2-x_3-4\right|}{3}$

Wir setzen die Koordinaten von $P$ ein.

Der Abstand soll $d=3$ betragen.

$\begin{array}{lll} 3=\dfrac{\left|2k+10-k-4\right|}{3}\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Für $k=3$ und für $k=-15$ ist $P$ genau

3 LE von $E$ entfernt.

Höhe bestimmen

Die Formel für den Flächeninhalt eines Dreiecks lautet $A=\frac{1}{2}\cdot g\cdot h$ .

Wir benutzen $\overline{AB}$ als Grundseite.

Die Höhe $h$ steht folglich senkrecht

auf $\overline{AB}$ und verläuft durch $C$ . Wir fällen

also das Lot von $C$ auf $\overline{AB}$ .

1. Schritt: Gerade $g$ durch $A$ und $B$ bestimmen

$\begin{array}{rll} g:\overrightarrow{x}=&\overrightarrow{OA}+r\cdot\overrightarrow{AB}\\ =&\left(\begin{array}{r} 2\\ 1\\ 0\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 10\\ -10\\ 5\\ \end{array}\right) \end{array}$

2. Schritt: Lot von $C$ auf $g$ fällen

Jeder Punkt $Q$ auf $g$ hat die Koordinaten $Q\left(2+10r \mid 1-10r \mid 5r\right)$ .

Wir bestimmen den Verbindungsvektor

von $Q$ und $C$ :

$\overrightarrow{CQ}=\left(\begin{array}{r} 2+10r-6\\ 1-10r-7\\ 5r-10\\ \end{array}\right)=\left(\begin{array}{r} -4+10r\\ -6-10r\\ -10+5r\\ \end{array}\right)$

Der Vektor $\overrightarrow{CQ}$ soll senkrecht auf die Gerade $g$ stehen, sein Skalarprodukt mit dem Richtungsvektor der Geraden soll also Null ergeben:

$\begin{array}{rll} 0=&\left(\begin{array}{r} -4+10r\\ -6-10r\\ -10+5r\\ \end{array}\right)\cdot\left(\begin{array}{r} 10\\ -10\\ 5\\ \end{array}\right)\\[5pt] 0=&-40+100r+60+100r-50\end{array}$ $\begin{array}{rll} &+25r\\[5pt] 0=&-30+225r\quad\mid +30\\[5pt] 30=&225r\quad\mid :225\\[5pt] \frac{2}{15}=&r \end{array}$

Der Betrag von $\overrightarrow{CQ}$ ist die Höhe des Dreiecks:

$\left|\overrightarrow{CQ}\right|=\left|\left(\begin{array}{r} -4+10\cdot\frac{2}{15}\\ -6-10\cdot\frac{2}{15}\\ -10+5\cdot\frac{2}{15}\\ \end{array}\right)\right|=$

Vollständige Lösung anzeigen

Für den Flächeninhalt des

Dreiecks gilt also:

$A=\frac{1}{2}\cdot\left|\overrightarrow{AB}\right|\cdot\sqrt{148}=$ $\frac{1}{2}\cdot\sqrt{100+100+25}\cdot\sqrt{148}=$ $\frac{1}{2}\cdot15\cdot\sqrt{148}\approx91,275$

Der Flächeninhalt des Dreiecks beträgt etwa $91,275$ FE.

Höhe des Parallelogramms bestimmen

Der Flächeninhalt eines Parallelogramms wird bestimmt mit der Formel $A=g\cdot h$ . Wir benutzen die Seite $\overline{AB}$ als Grundfläche. Als Höhe benutzen wir den Abstand des Punktes $C$ zu der Geraden durch $A$ und $B$ .

1. Schritt: Gerade $g$ durch $A$ und $B$ bestimmen

$\begin{array}{rll} g:\overrightarrow{x}=&\overrightarrow{OA}+r\cdot\overrightarrow{AB}\\ =&\left(\begin{array}{r} 1\\ 4\\ 0\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 0\\ 4\\ -8\\ \end{array}\right) \end{array}$

2. Schritt: Abstand von $C$ zu $g$ bestimmen

Jeder Punkt $Q$ auf $g$ hat die Koordinaten $Q\left(1 \mid 4+4r \mid -8r\right)$ . Wir bestimmen zunächst den Verbindungsvektor von $Q$ und $C$ :

$\overrightarrow{CQ}=\left(\begin{array}{r} 1-1\\ 4+4r-7\\ -8r-(-1)\\ \end{array}\right)=\left(\begin{array}{r} 0\\ -3+4r\\ 1-8r\\ \end{array}\right)$

Der Vektor $\overrightarrow{CQ}$ soll senkrecht zu $g$ verlaufen, sein Skalarprodukt mit dem Richtungsvektor von $g$ muss also Null ergeben:

$\begin{array}{rll} 0=&\left(\begin{array}{r} 0\\ -3+4r\\ 1-8r\\ \end{array}\right)\circ\left(\begin{array}{r} 0\\ 4\\ -8\\ \end{array}\right)\\[5pt] 0=&-12+16r-8+64r\\[5pt] 0=&-20+80r&\quad\mid\; +20\\[5pt] 20=&80r&\quad\mid\; :80\\[5pt] \frac{1}{4}=&r \end{array}$

Der Betrag des Vektors $\overrightarrow{CQ}$ ist die Höhe des Parallelogramms:

$\left|\overrightarrow{CQ}\right|=\left|\left(\begin{array}{r} 0\\ -2\\ -1\\ \end{array}\right)\right|=\sqrt{4+1}=\sqrt5$

Für den Flächeninhalt des Parallelogramms gilt also:

$A$ = $\left|\overrightarrow{AB}\right|\cdot\sqrt5$ = $\sqrt{16+64}\cdot\sqrt5$ = $\sqrt{80}\cdot\sqrt{5}$ = $\sqrt{400}=20 FE$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?