Ganzrationale Funktionen
1.
Das Schaubild der Funktion  mit
mit  stellt im Bereich
stellt im Bereich  den Querschnitt einer Achterbahn dar.
den Querschnitt einer Achterbahn dar.
a)
Skizziere  im angegebenen Intervall in einem Koordinatensystem.
im angegebenen Intervall in einem Koordinatensystem.
b)
An der Stelle, an der die Kurve mit einer Steigung von  fällt, werden die Leute in der Achterbahn fotografiert. Bestimme die Stelle, an der das Foto geschossen wird.
fällt, werden die Leute in der Achterbahn fotografiert. Bestimme die Stelle, an der das Foto geschossen wird.
c)
Die Leute kreischen immer dann am lautesten, wenn sie sich gerade an einem Punkt befinden, der sich genau zwischen Steigung und Gefälle befindet.
Sie werden also hochgezogen und schreien dann los, wenn es bergab geht.
Wo schreien die Leute am lautesten?
Sie werden also hochgezogen und schreien dann los, wenn es bergab geht.
Wo schreien die Leute am lautesten?
d)
Die Achterbahn wird am Punkt mit der größten Steigung am meisten beschleunigt. Bestimme diesen Punkt.
2.
Das Schaubild der Funktion  mit
mit  stellt den Querschnitt eines Gebirges dar.
stellt den Querschnitt eines Gebirges dar.
a)
Skizziere  in einem Koordinatensystem.
in einem Koordinatensystem.
b)
Bestimme, in welchen Bereichen das Gebirge steigt bzw. fällt.
c)
In der Kuhle, welche sich zwischen zwei Nullstellen befindet, fließt ein Bach, der das Gebirge ausspült.
Wie breit ist der Fluss? Wie tief ist er an der tiefsten Stelle?
Wie breit ist der Fluss? Wie tief ist er an der tiefsten Stelle?
3.
Eine Textilfirma hat einen neuen Hut entworfen. Die Krempe des Hutes lässt sich mit der Funktion  mit
mit  beschreiben.
beschreiben.
a)
Der Hut selbst lässt sich wie folgt skizzieren:
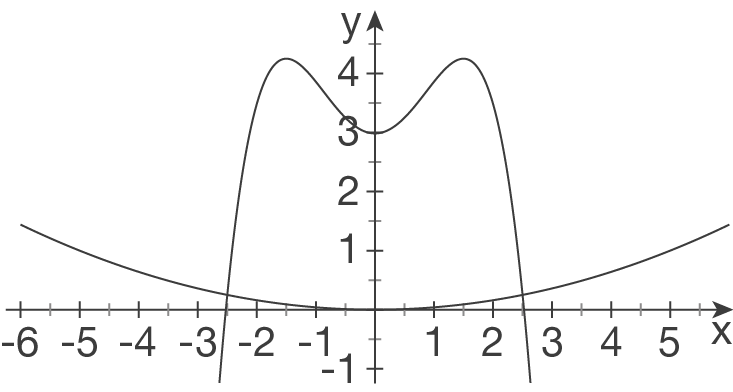 Bei
Bei  schneiden sich die beiden Funktionen. Die höchsten Stellen des Hutes befinden sich bei
schneiden sich die beiden Funktionen. Die höchsten Stellen des Hutes befinden sich bei  .
.
Die Form des Hutes kann mit einer ganzrationalen Funktion 4. Grades beschrieben werden, die achsensymmetrisch zur -Achse ist.
-Achse ist.
Gib eine Funktionsgleichung an, runde die Werte gegebenenfalls.

Die Form des Hutes kann mit einer ganzrationalen Funktion 4. Grades beschrieben werden, die achsensymmetrisch zur
Gib eine Funktionsgleichung an, runde die Werte gegebenenfalls.
b)
Wie groß ist in diesem Querschnitt der Flächeninhalt des Hutes (also der eingeschlossenen Fläche)?
c)
Wo fällt der Hut am steilsten ab?
4.
Zwischen zwei dünnen Bäumen ist eine Schnur gespannt, auf die sich immer wieder gerne Vögel setzen. Mit jedem Vogel, der sich auf die Schnur setzt, biegt sie sich etwas weiter nach unten durch.
Unten sind die Kurven der Schnur gezeichnet; zeigt die Schnur, auf der 1 Vogel sitzt,
zeigt die Schnur, auf der 1 Vogel sitzt,  zeigt die Schnur, auf der 2 Vögel sitzen und
zeigt die Schnur, auf der 2 Vögel sitzen und  zeigt die Schnur, auf der 3 Vögel sitzen.
zeigt die Schnur, auf der 3 Vögel sitzen.
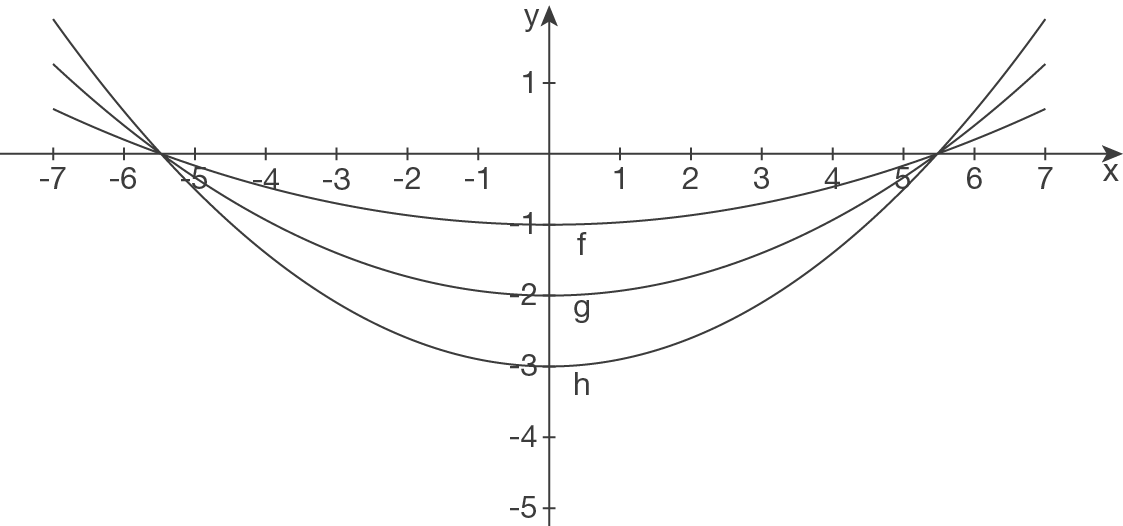
Unten sind die Kurven der Schnur gezeichnet;

a)
Die Schnur lässt sich durch eine ganzrationale Funktion 2. Grades beschreiben, die achsensymmetrisch zur  -Achse ist.
-Achse ist.
 geht durch die Punkte
geht durch die Punkte  und
und  .
.
 geht durch die Punkte
geht durch die Punkte  und
und  .
.
 geht durch die Punkte
geht durch die Punkte  und
und  .
.
Stelle für ,
,  ,
,  je eine Funktionsgleichung auf.
je eine Funktionsgleichung auf.
Stelle für
b)
Ausgehend von diesen drei Funktionsgleichungen lässt sich die Funktionsgleichung einer Kurvenschar formulieren. Diese enthält den Parameter  , wobei
, wobei  für die Anzahl der Vögel steht.
für die Anzahl der Vögel steht.
Stelle die Funktionsgleichung dieser Kurvenschar auf.
Stelle die Funktionsgleichung dieser Kurvenschar auf.
c)
Die Schnur ist auf Höhe der  -Achse an den Bäumen festgemacht.
-Achse an den Bäumen festgemacht.
Beugen sich die Bäume mit dem Gewicht der Vögel?
Beugen sich die Bäume mit dem Gewicht der Vögel?
5.
Eine Autorennstrecke lässt sich durch die beiden Funktionen  und
und  beschreiben. Die Strecke wird dabei im Uhrzeigersinn durchfahren.
beschreiben. Die Strecke wird dabei im Uhrzeigersinn durchfahren.
a)
Skizziere die beiden Funktionen in einem Koordinatensystem.
b)
Bestimme die Koordinaten der Punkte, die am weitesten links bzw. rechts außen liegen.
c)
Bestimme die Koordinaten der Punkte, die am weitesten oben bzw. unten liegen.
d)
Eines der Autos fliegt bei  tangential aus der Bahn. Bei
tangential aus der Bahn. Bei  sind in einer geraden Linie Reifen aufgestellt.
sind in einer geraden Linie Reifen aufgestellt.
An welcher Stelle trifft das Auto auf die Reifen?
An welcher Stelle trifft das Auto auf die Reifen?
e)
Ein weiteres Auto landet bei  in der Reifenmauer.
in der Reifenmauer.
Wo ist dieses Auto aus der Kurve geflogen?
Wo ist dieses Auto aus der Kurve geflogen?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
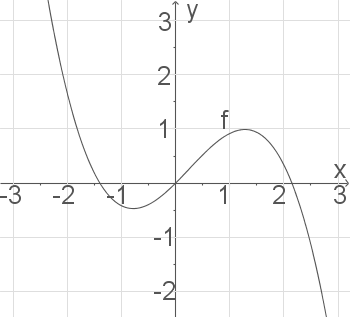
b)
Wir müssen zunächst die Stelle bestimmen, an der  die Steigung
die Steigung  besitzt. Dies tun wir, indem wir die erste Ableitung bilden, da uns die Ableitung immer die Steigung angibt. Wir setzen also
besitzt. Dies tun wir, indem wir die erste Ableitung bilden, da uns die Ableitung immer die Steigung angibt. Wir setzen also  und lösen nach
und lösen nach  auf.
Stelle mit Steigung
auf.
Stelle mit Steigung  bestimmen
bestimmen
 Ableitungsfunktion bilden
Ableitungsfunktion bilden
 Gleichsetzen
Gleichsetzen
Bei  und bei
und bei  werden Fotos geschossen.
werden Fotos geschossen.
c)
Ein Punkt, an dem eine Kurve nach einer Steigung wieder fällt, ist ein Hochpunkt. Um diesen zu berechnen, setzen wir  und lösen nach
und lösen nach  auf.
Hochpunkt bestimmen
auf.
Hochpunkt bestimmen
 Ableitungsfunktion bilden
Ableitungsfunktion bilden

 Notwendige Bedingung: 1. Ableitung
Notwendige Bedingung: 1. Ableitung  setzen
setzen
 -
- -Formel anwenden:
-Formel anwenden:
 Hinreichende Bedingung: auf echten Hochpunkt prüfen
Hinreichende Bedingung: auf echten Hochpunkt prüfen
d)
Der Punkt mit der größten Steigung ist der Wendepunkt. Diesen bestimmen wir, indem wir  setzen.
Wendepunkt bestimmen
setzen.
Wendepunkt bestimmen
 Ableitungsfunktion bilden
Ableitungsfunktion bilden

 Notwendige Bedingung: 2. Ableitung
Notwendige Bedingung: 2. Ableitung  setzen
setzen

 Hinreichende Bedingung: auf echten Wendepunkt prüfen
Hinreichende Bedingung: auf echten Wendepunkt prüfen
2.
a)
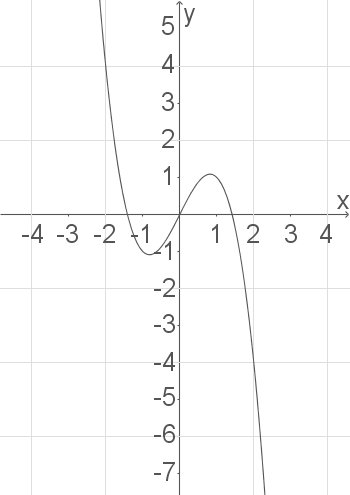
b)
Wir sehen im Schaubild, dass die Funktion erst fällt (bis zum Tiefpunkt), dann kurz ansteigt (bis zum Hochpunkt) und dann wieder fällt (ab dem Hochpunkt). Wir bestimmen also die Koordinaten der Extrempunkte.
Extrema bestimmen
 Ableitungsfunktionen bilden
Ableitungsfunktionen bilden

 Notwendige Bedingung: 1. Ableitung
Notwendige Bedingung: 1. Ableitung  setzen
setzen
 Hinreichende Bedingung: auf echten Hoch- bzw. Teifpunkt prüfen
Daraus folgt:
Hinreichende Bedingung: auf echten Hoch- bzw. Teifpunkt prüfen
Daraus folgt:
 ist monoton fallend für
ist monoton fallend für 
 ist monoton steigend für
ist monoton steigend für 
 ist monoton fallend für
ist monoton fallend für 
c)
Breite des Flusses berechnen
Die Breite des Flusses ist der Abstand, den die Nullstellen voneinander haben. Wir bestimmen diese also zunächst:
 Nullstellen bestimmen
Satz vom Nullprodukt: Ein Produkt ist 0, wenn einer seiner Faktoren 0 ist.
Nullstellen bestimmen
Satz vom Nullprodukt: Ein Produkt ist 0, wenn einer seiner Faktoren 0 ist.

 Abstand
Abstand  zwischen den Nullstellen bestimmen
zwischen den Nullstellen bestimmen
 Der Fluss ist
Der Fluss ist  LE breit.
Tiefe des Baches berechnen
Um die Tiefe des Baches zu errechnen, bestimmen wir die
LE breit.
Tiefe des Baches berechnen
Um die Tiefe des Baches zu errechnen, bestimmen wir die  -Koordinate des Tiefpunktes.
-Koordinate des Tiefpunktes.

 -Wert des Tiefpunktes bestimmen
An der tiefsten Stelle ist der Bach ca. 1,09 m tief.
-Wert des Tiefpunktes bestimmen
An der tiefsten Stelle ist der Bach ca. 1,09 m tief.
3.
a)
Funktionsgleichung aufstellen
Wir wissen, dass es sich um eine ganzrationale Funktion 4. Grades handelt, die achsensymmetrisch zur  -Achse ist. Somit ergibt sich die allgemeine Gleichung:
-Achse ist. Somit ergibt sich die allgemeine Gleichung:
 Sehen wir uns nun die Bedingungen an, die gegeben sind:
Sehen wir uns nun die Bedingungen an, die gegeben sind:
Wir haben vier Punkte gegeben, die auf der Kurve liegen. Da die Funktion achsensymmetrisch zur -Achse ist und die beiden Punkte jeweils die gleichen
-Achse ist und die beiden Punkte jeweils die gleichen  -Werte haben, nur mit anderen Vorzeichen, benutzen wir jeweils nur einen der beiden. Weiterhin wissen wir, dass einer dieser beiden Punkte ein Hochpunkt ist. Ein Hochpunkt besitzt die Steigung 0. Wir haben also 3 verschiedene Bedingungen gegeben, die wir nun nacheinander in diese allgemeine Gleichung einsetzen. Wir beginnen mit dem einsetzen der Steigung in die 1. Ableitung.
Schritt 1: 1. Ableitung bilden
-Werte haben, nur mit anderen Vorzeichen, benutzen wir jeweils nur einen der beiden. Weiterhin wissen wir, dass einer dieser beiden Punkte ein Hochpunkt ist. Ein Hochpunkt besitzt die Steigung 0. Wir haben also 3 verschiedene Bedingungen gegeben, die wir nun nacheinander in diese allgemeine Gleichung einsetzen. Wir beginnen mit dem einsetzen der Steigung in die 1. Ableitung.
Schritt 1: 1. Ableitung bilden
 Schritt 2:
Schritt 2:  einsetzen
In diese Gleichung setzen wir nun den nächsten Punkt ein, den wir gegeben haben, nämlich den Schnittpunkt der beiden Kurven. Da wir hier nur den
einsetzen
In diese Gleichung setzen wir nun den nächsten Punkt ein, den wir gegeben haben, nämlich den Schnittpunkt der beiden Kurven. Da wir hier nur den  -Wert gegeben haben, rechnen wir zunächst den
-Wert gegeben haben, rechnen wir zunächst den  -Wert aus.
Schritt 3:
-Wert aus.
Schritt 3:  bestimmen; entspricht
bestimmen; entspricht 
 Schritt 4:
Schritt 4:  und
und  einsetzen in
einsetzen in  Als neue allgemeine Gleichung gilt nun also:
Wir setzen nun den letzten Punkt ein, den wir gegeben haben:
Schritt 5:
Als neue allgemeine Gleichung gilt nun also:
Wir setzen nun den letzten Punkt ein, den wir gegeben haben:
Schritt 5:  und
und  einsetzen in
einsetzen in  Wir lösen nun nach den restlichen Unbekannten auf.
Schritt 6:
Wir lösen nun nach den restlichen Unbekannten auf.
Schritt 6:  einsetzen in
einsetzen in  Schritt 7:
Schritt 7:  einsetzen in
einsetzen in 
 Daraus folgt die Funktionsgleichung
Daraus folgt die Funktionsgleichung

Wir haben vier Punkte gegeben, die auf der Kurve liegen. Da die Funktion achsensymmetrisch zur
b)
Flächeninhalt bestimmen
c)
Hier ist nach dem Punkt mit der größten Steigung gefragt. Dies ist immer der Wendepunkt einer Funktion.
Wendepunkt bestimmen
Schritt 1: Ableitungen bilden
Schritt 2:  setzen
Da nur nach der Stelle gefragt ist, wo das Schaubild am stärksten fällt, ist für uns nur die Lösung
setzen
Da nur nach der Stelle gefragt ist, wo das Schaubild am stärksten fällt, ist für uns nur die Lösung  relevant. Bei
relevant. Bei  steigt das Schaubild.
Schritt 3:
steigt das Schaubild.
Schritt 3:  auf echten Wendepunkt prüfen
An der Stelle
auf echten Wendepunkt prüfen
An der Stelle  fällt der Hut am steilsten ab.
fällt der Hut am steilsten ab.
4.
a)
Funktionsgleichungen bestimmen
Wir wissen, dass es sich bei allen drei Funktionen um ganzrationale Funktionen zweiten Grades handelt, die achsensymmetrisch zur  -Achse sind. Deshalb lautet die allgemeine Funktionsgleichung:
-Achse sind. Deshalb lautet die allgemeine Funktionsgleichung:
 .
Wir können nun die jeweilige Funktionsgleichung bestimmen, indem wir die Koordinaten der gegebenen Punkte in die allgemeine Funktionsgleichung einsetzen und nach den Unbekannten lösen. Beginnen wir nun mit der Funktionsgleichung von
.
Wir können nun die jeweilige Funktionsgleichung bestimmen, indem wir die Koordinaten der gegebenen Punkte in die allgemeine Funktionsgleichung einsetzen und nach den Unbekannten lösen. Beginnen wir nun mit der Funktionsgleichung von 
 Funktionsgleichung von
Funktionsgleichung von  bestimmen
Schritt 1:
bestimmen
Schritt 1:  verwenden:
verwenden:  und
und  einsetzen
einsetzen
 Daraus folgt die neue allgemeine Gleichung
Daraus folgt die neue allgemeine Gleichung
 Schritt 2:
Schritt 2:  verwenden:
verwenden:  und
und  einsetzen
Daraus folgt die Funktionsgleichung
einsetzen
Daraus folgt die Funktionsgleichung

 Funktionsgleichung von
Funktionsgleichung von  bestimmen
Schritt 1:
bestimmen
Schritt 1:  verwenden:
verwenden:  und
und  einsetzen
einsetzen
 Daraus folgt die neue allgemeine Gleichung
Daraus folgt die neue allgemeine Gleichung
 Schritt 2:
Schritt 2:  verwenden:
verwenden:  und
und  einsetzen
Daraus folgt die Funktionsgleichung
einsetzen
Daraus folgt die Funktionsgleichung

 Funktionsgleichung von
Funktionsgleichung von  bestimmen
Schritt 1:
bestimmen
Schritt 1:  verwenden:
verwenden:  und
und  einsetzen
einsetzen
 Daraus folgt die neue allgemeine Gleichung
Daraus folgt die neue allgemeine Gleichung
 Schritt 2:
Schritt 2:  verwenden:
verwenden:  und
und  einsetzen
Daraus folgt die Funktionsgleichung
einsetzen
Daraus folgt die Funktionsgleichung

b)
Vergleichen wir zunächst die drei Funktionsgleichungen.:
c)
Die Position der Befestigungen an den Bäumen ist "sozusagen" der Schnittpunkt der Kurven mit der  -Achse. Wir bestimmen also die Nullstellen von
-Achse. Wir bestimmen also die Nullstellen von  . Wenn diese Nullstellen unabhängig von
. Wenn diese Nullstellen unabhängig von  immer gleich sind, beugen sich die Bäume nicht mit.
Nullstellen bestimmen
immer gleich sind, beugen sich die Bäume nicht mit.
Nullstellen bestimmen
5.
a)
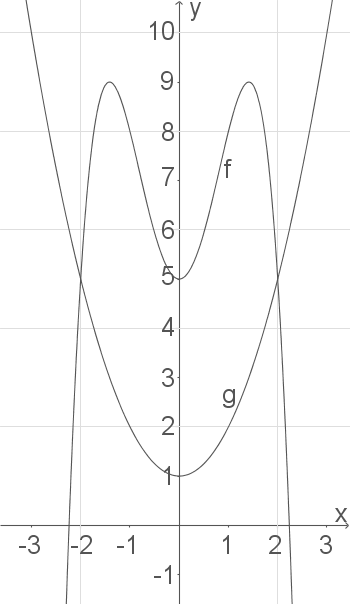
b)
Die Skizze verrät uns, dass die Punkte links bzw. rechts außen die Schnittpunkte der beiden Funktionsgraphen sind. Diese bestimmen wir, indem wir die Funktionsgleichungen gleichsetzen.
Schnittpunkte bestimmen
 -
- -Formel anwenden
Resubstitution durchführen
Schritt 2:
-Formel anwenden
Resubstitution durchführen
Schritt 2:  -Werte bestimmen
-Werte bestimmen

 -Wert für
-Wert für  bestimmen
bestimmen


 -Wert für
-Wert für  bestimmen
bestimmen
 Daraus ergeben sie die Punkte
Daraus ergeben sie die Punkte  und
und  .
.
c)
Die Punkte, die am weitesten oben bzw. unten liegen sind die Hochpunkte von  und der Tiefpunkt von
und der Tiefpunkt von  .
.
 Hochpunkte von
Hochpunkte von  bestimmen
Schritt 1: Ableitungen bilden
Schritt 2: Notwendige Bedingung:
bestimmen
Schritt 1: Ableitungen bilden
Schritt 2: Notwendige Bedingung:  setzen
Satz vom Nullprodukt: Ein Produkt ist
setzen
Satz vom Nullprodukt: Ein Produkt ist  , wenn einer seiner Faktoren
, wenn einer seiner Faktoren  ist.
Schritt 3: Hinreichende Bedingung:
ist.
Schritt 3: Hinreichende Bedingung:  -Werte auf echte Hochpunkte überprüfen
-Werte auf echte Hochpunkte überprüfen
 auf echten Hochpunkt überprüfen
Schritt 4:
auf echten Hochpunkt überprüfen
Schritt 4:  -Werte bestimmen
-Werte bestimmen
 -Wert für
-Wert für  bestimmen
bestimmen
 -Wert für
-Wert für  bestimmen
Daraus folgen die Hochpunkte
bestimmen
Daraus folgen die Hochpunkte  und
und  .
.
 Tiefpunkt von
Tiefpunkt von  bestimmen
Schritt 1: Ableitungen bilden
Schritt 2: Notwendige Bedingung:
bestimmen
Schritt 1: Ableitungen bilden
Schritt 2: Notwendige Bedingung:  setzen
setzen
 Schritt 3: Hinreichende Bedingung:
Schritt 3: Hinreichende Bedingung:  auf echten Tiefpunkt überprüfen
auf echten Tiefpunkt überprüfen
 Schritt 4:
Schritt 4:  -Wert von
-Wert von  bestimmen
bestimmen
 Daraus ergibt sich der Tiefpunkt
Daraus ergibt sich der Tiefpunkt  .
.
d)
Da das Auto bei  tangential aus der Bahn fliegt, wird die Flugbahn idurch die Gleichung der Tangente beschrieben, die das Schaubild an der Stelle
tangential aus der Bahn fliegt, wird die Flugbahn idurch die Gleichung der Tangente beschrieben, die das Schaubild an der Stelle  berührt. Da ein Auto nur in den Reifen landen kann, wenn es in dem Teil der Bahn aus der Bahn fliegt, der von dem Graphen von
berührt. Da ein Auto nur in den Reifen landen kann, wenn es in dem Teil der Bahn aus der Bahn fliegt, der von dem Graphen von  beschrieben wird, ist hier eine Tangente an den Graphen von
beschrieben wird, ist hier eine Tangente an den Graphen von  gesucht. Dies kannst du dir anhand der Skizze der beiden Graphen klarmachen. Der Schnittpunkt der Tangente mit der Geraden zu
gesucht. Dies kannst du dir anhand der Skizze der beiden Graphen klarmachen. Der Schnittpunkt der Tangente mit der Geraden zu  ist dann die Stelle, an der das Auto auf die Reifen trifft.
ist dann die Stelle, an der das Auto auf die Reifen trifft.
Die gesuchte Tangente lässt sich mit der allgemeinen Tangentengleichung bestimmen: Schritt 1: Tangente an in
in  anlegen
anlegen
Die gesuchte Tangente lässt sich mit der allgemeinen Tangentengleichung bestimmen: Schritt 1: Tangente an
e)
Auch hier ist eine Tangente verlangt, die  berührt und durch den Punkt
berührt und durch den Punkt  geht, der nicht auf
geht, der nicht auf  liegt. Diese Tangentengleichung lässt sich ebenfalls mit der allgemeinen Tangentengleichung bestimmen. Dazu werden die Koordinaten von
liegt. Diese Tangentengleichung lässt sich ebenfalls mit der allgemeinen Tangentengleichung bestimmen. Dazu werden die Koordinaten von  für
für  und
und  eingesetzt.
Schritt 1: Tangente durch
eingesetzt.
Schritt 1: Tangente durch  ermitteln
ermitteln