Vermischte Aufgaben

Gegeben ist die Funktion $f$ mit $f\left(x\right)=x^3+3x^2+4$ .

Skizziere $f$ in einem Koordinatensystem.

Wähle einen geeigneten Startwert und bestimme die Nullstelle von $f$ .

Bestimme mit Hilfe der Keplerschen Fassregel den Inhalt der Fläche, die von $f$ und der $x$ -Achse zwischen der Nullstelle und $x=0$ eingeschlossen wird.

Der Eingang einer Höhle kann mit dem Schaubild der Funktion $f$ mit $f\left(x\right)=-\dfrac{1}{2}\left(\mathrm e^{x}-x^3-x\right)+3$ beschrieben werden.

Skizziere das Schaubild von $f$ in einem Koordinatensystem.

Wähle geeignete Startwerte und bestimme mit Hilfe des Newton-Verfahrens die Nullstellen von $f$ .

Bestimme mit Hilfe der Keplerschen Fassregel den Flächeninhalt des Eingangs. Mit einem GTR ausgerechnet beträgt das Ergebnis etwa 29,2 FE. Vergleiche dieses Ergebnis mit deinem. Was sagt dies über die Keplersche Fassregel aus?

In einem Park wurde ein Wasserlauf gebaut, der terrassenförmig einen Berg hinab in einen Fluss fließt. Der Querschnitt dieses Wasserlaufs lässt sich für $-10\leq x\leq6$ mit der Funktion $f$ mit $f\left(x\right)=\sin{\left(x\right)}+x+3$ beschreiben. Der Wasserlauf ist $10m$ breit; eine Einheit im Koordinatensystem entspricht einem Meter.

Skizziere $f$ in einem Koordinatensystem.

Bevor der Wasserlauf angelegt wurde, befand sich das gesamte Gelände etwa auf Höhe der $x$ -Achse. Der Wasserlauf wurde geschaffen, indem auf der einen Seite Erde abgegraben wurde und auf der anderen Seite Erde aufgehäuft wurde. Wo wurde Erde abgetragen? Wie viel Erde war das? Bestimme dieses Volumen mit Hilfe der Keplerschen Fassregel.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$f\left(x\right)=x^3+3x^2+4$

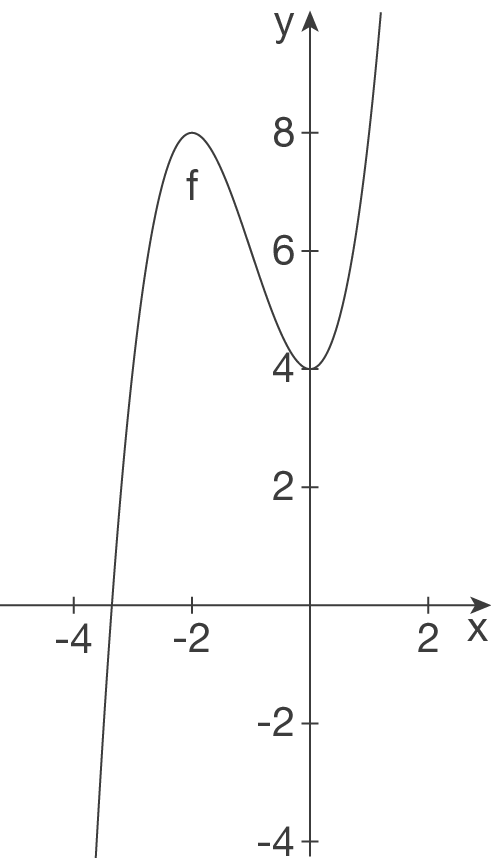
Graph einer Funktion mit einer Kurve, die durch die Achsen verläuft.

1. Schritt: Ableitung bilden

$\begin{array}{rlll} f\left(x\right)&=x^3+3x^2+4\\[3pt] f‘\left(x\right)&=3x^2+6x \end{array}$

2. Schritt: Startwert wählen

$x_0=-3$

3. Schritt: Newton‘sches Näherungsverfahren anwenden

$\begin{array}{rlll} x_{n+1}&=x_{n}-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Da es sehr zeitaufwendig ist, diese Annäherung von Hand durchzuführen und man sich dabei leicht verrechnet, überlassen wir das dem Taschenrechner.
Dazu führen wir nacheinander folgende Schritte aus:

Wir speichern den Startwert $-3$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS $-\left(\text{ANS}^3+3\cdot\text{ANS}^2+4\right)$ / $\left(3\cdot\text{ANS}^2+6\cdot\text{ANS}\right)$ .
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*=-3,3553$

Die Keplersche Fassregel lautet:

$\displaystyle\int_{a}^{b}{f\left(x\right)}dx=\;...$

Vollständige Lösung anzeigen

Unser $a=-3,3553$ , unser $b=0$ .

Am besten berechnest du zuerst separat $f(a)$ , $f(b)$ und $f(\frac{a+b}{2})$ .

Vollständige Lösung anzeigen

Damit ergibt sich:

$\begin{array}{rlllllll} \displaystyle\int_{-3,3553}^{0}f\left(x\right)dx&=19,5087 \end{array}$

Vollständige Lösung anzeigen

$f\left(x\right)=-\dfrac{1}{2}\left(\mathrm e^{x}-x^3-x\right)+3$

$\blacktriangleright$ 1. Nullstelle bestimmen

1. Schritt: Ableitung bilden

$\begin{array}{rlll} f\left(x\right)&=-\dfrac{1}{2}\left(\mathrm e^x-x^3-x\right)+3\\[5pt] f‘\left(x\right)&=-\dfrac{1}{2}\left(\mathrm e^x-3x^2-1\right) \end{array}$

2. Schritt: Startwert wählen

$x_0=-2$

3. Schritt: Newton‘sches Näherungsverfahren anwenden

$\begin{array}{rlll} x_{n+1}&=x_{n}-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Da wir uns bei der Berechnung per Hand sehr leicht verrechnen könnten und es viel Arbeit machen würde, überlassen wir dies dem Taschenrechner.
Dazu führen wir nacheinander folgende Schritte aus:

Vollständige Lösung anzeigen

Wir erhalten als Ergebnis:
${x_1}^*=-1,6120$

$\blacktriangleright$ 2. Nullstelle bestimmen

1. Schritt: Startwert wählen

$x_0=5$

2. Schritt: Newton‘sches Näherungsverfahren anwenden

$\begin{array}{rlll} x_{n+1}&=x_{n}-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Da wir uns bei der Berechnung per Hand sehr leicht verrechnen könnten und es viel Arbeit machen würde, überlassen wir dies dem Taschenrechner.
Dazu führen wir nacheinander folgende Schritte aus:

Vollständige Lösung anzeigen

Wir erhalten als Ergebnis:
${x_2}^*=4,7977$

Die Keplersche Fassregel lautet:

$\displaystyle\int_{a}^{b}{f\left(x\right)}dx=\;...$

Vollständige Lösung anzeigen

Unser $a=-1,612$ , unser $b=4,7977$ .

Am besten berechnest du zuerst separat $f(a)$ , $f(b)$ und $f(\frac{a+b}{2})$ .

Vollständige Lösung anzeigen

Damit ergibt sich:

$\begin{array}{rlllllll} \displaystyle\int_{-1,612}^{4,7977}f\left(x\right)dx&=\;... \end{array}$

Vollständige Lösung anzeigen

Wenn wir die Werte miteinander vergleichen, erkennen wir, dass sie stark voneinander abweichen.

Dies liegt daran, dass die Keplersche Fassregel nur ein Näherungsverfahren ist, das für Polynome und einfache Funktionen sehr gut funktioniert, aber bei komplizierteren Funktionen sehr ungenau wird.

$f\left(x\right)=\sin{\left(x\right)}+x+3$

Der Bereich, in dem Erde abgetragen wurde, ist genau der, der unterhalb der $x$ -Achse liegt. Wir bestimmen also die Nullstelle, um diesen Bereich genau bestimmen zu können.

$\blacktriangleright$ Nullstelle bestimmen

1. Schritt: Ableitung bilden

$\begin{array}{rlll} f\left(x\right)&=\sin{\left(x\right)}+x+3\\[5pt] f‘\left(x\right)&=\cos{\left(x\right)}+1 \end{array}$

2. Schritt: Startwert wählen

$x_0=-2$

3. Schritt: Newton‘sches Näherungsverfahren anwenden

$\begin{array}{rlll} x_{n+1}&=x_{n}-\dfrac{f\left(x_n\right)}{f‘\left(x_n\right)}\\[5pt] x_{n+1}&=x_n-\dfrac{\sin\left(x_n\right)+x_n}{\cos\left(x_n\right)+1} \end{array}$

Da wir uns bei der Berechnung per Hand sehr leicht verrechnen könnten und es viel Arbeit machen würde, überlassen wir dies dem Taschenrechner.
Dazu führen wir nacheinander folgende Schritte aus:

Wir speichern den Startwert $-2$ als ANS (letztes Ergebnis).
Wir geben folgendes ein: ANS $-\left(\sin\left(\text{ANS}\right)+\text{ANS}+3\right)$ / $\left(\cos\left(\text{ANS}\right)+1\right)$ .
Nun drücken wir so lange ENTER, bis immer wieder die gleiche Zahl als Ergebnis herauskommt.

Wir erhalten als Ergebnis:
$x^*=-2,18$

Im Bereich $-10\leq x\leq-2,18$ wurde Erde abgetragen.

$\blacktriangleright$ Volumen der Erde bestimmen

Um das Volumen der Erde zu bestimmen, berechnen wir den Inhalt der Fläche, die von der $x$ -Achse und der Kurve zwischen -10 und -2,18 eingeschlossen wird und multiplizieren sie mit der Breite des Wasserlaufs $(10m)$ .

Die Keplersche Fassregel lautet:

$\displaystyle\int_{a}^{b}{f\left(x\right)}dx=\;...$

Vollständige Lösung anzeigen

Unser $a=-10$ , unser $b=-2,18$ .

Am besten berechnest du zuerst separat $f(a)$ , $f(b)$ und $f(\frac{a+b}{2})$ .

Vollständige Lösung anzeigen

Damit ergibt sich:

$\begin{array}{rlllllll} \displaystyle\int_{-10}^{-2,18}f\left(x\right)dx&=\;... \end{array}$

Vollständige Lösung anzeigen

Um das Volumen der abgetragenen Erde zu erhalten, nehmen wir die eben berechnete Querschnittsfläche $(23,48m^2)$ mal $10m$ , da der Wasserlauf $10m$ breit ist:

Volumen=23,48m $^2\cdot10$ m

Volumen=234,8m $^3$

Vergleicht man dieses Ergebnis mit dem Ergebnis, das der GTR liefert ( $A=-24,43$ $\Rightarrow\;Volumen=244,3m^3$ ), so fällt auf, dass sich die Werte unterscheiden.

Dies liegt daran, dass die Keplersche Fassregel nur ein Näherungsverfahren darstellt und bei komplexeren Funktionen keine genauen Werte liefert.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?