Logarithmusfunktionen
Wenn du den Graph der natürlichen Logarithmusfunktion zeichnen willst, beachte folgende Punkte:
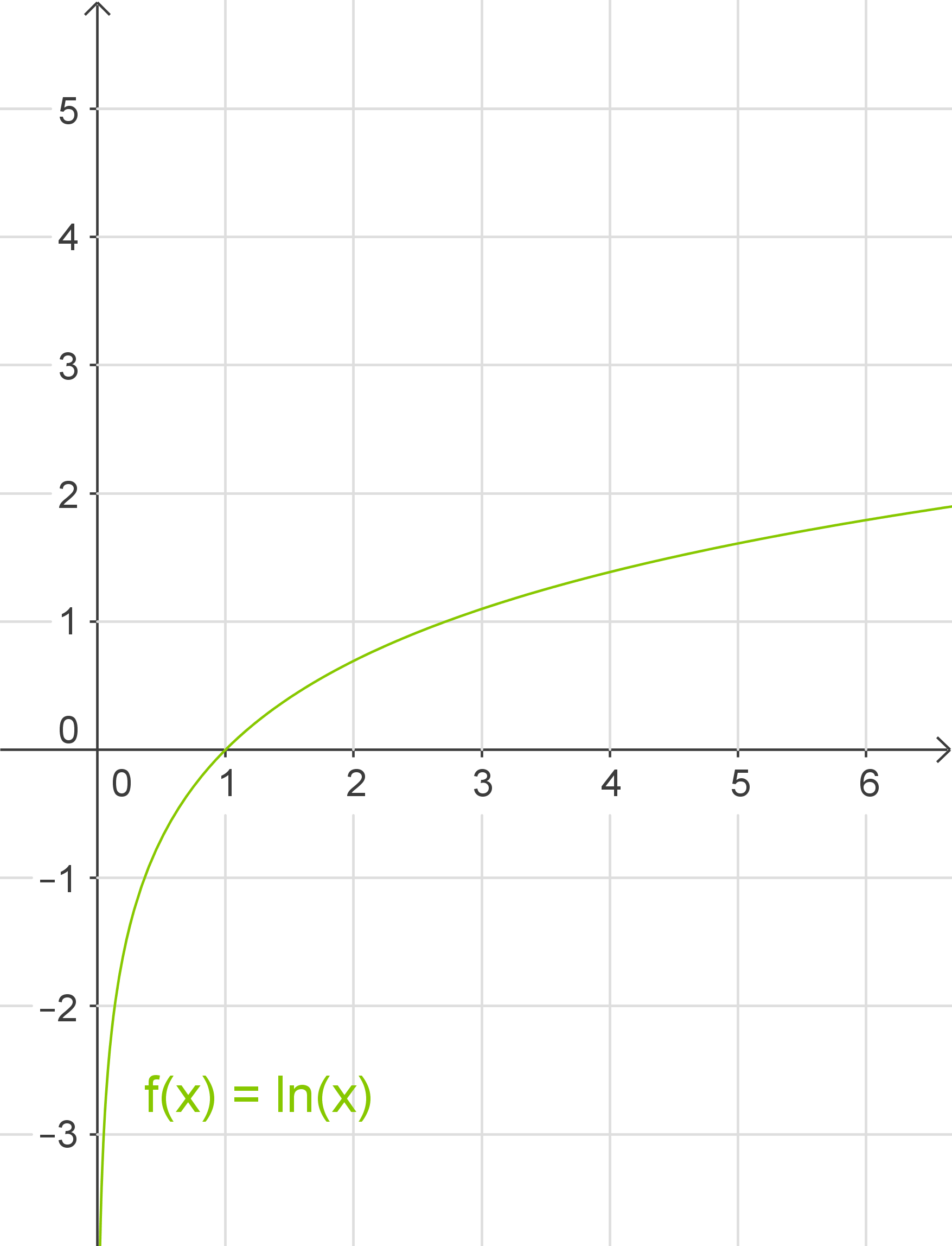
- Die Funktion
ist nur für Zahlen, die echt größer
sind, definiert. Sie schneidet die
-Achse an der Stelle
, hat als senkrechte Asymptote die
-Achse und ist streng monoton steigend.
- Verschiebungen in postive oder negative
-Richtung erkennst du an der Addition einer Konstanten
zu
.
. Der Graph wird nach rechts bzw. links verschoben, wenn eine Konstante
zum Numerus addiert wird:
- Streckungen in Richtung der y-Achse erkennst du, wenn die Funktion
mit einem Faktor
multipliziert wurde, Stauchungen in Richtung der
-Achse mit einem Faktor
:
. Ist der Numerus mit einem Faktor
multipliziert, so streckst du den Graphen entlang der
-Achse, mit einem Faktor
stauchst du den Graphen:
- Spiegelungen an der
-Achse werden durch ein negatives Vorzeichen der Logarithmusfunktion impliziert:
oder wenn der Kehrwert des Numerus gebildet wurde:
. Wird der Numerus mit einem negativen Vorzeichen multipliziert, spiegelst du den Graphen an der
-Achse
.
1.
Skizziere die Schaubilder folgender Funktionen und gib den Definitionsbereich an.






a)
b)
c)
d)
e)
f)
2.
Skizziere das Schaubild der Funktion und beschreibe, wie es aus dem Schaubild der  -Funktion hervorgeht.
-Funktion hervorgeht.






a)
b)
c)
d)
e)
f)
3.
Verschiebe das Schaubild der angegebenen Funktion wie gefordert und gib die Funktionsgleichung der neuen Funktion an.
 Verschiebung um 1 LE in positive
Verschiebung um 1 LE in positive  -Richtung („nach rechts“) und um 2 LE in positive
-Richtung („nach rechts“) und um 2 LE in positive  -Richtung („nach oben“).
-Richtung („nach oben“).
 Verschiebung um 3 LE in negative
Verschiebung um 3 LE in negative  -Richtung („nach links“) und um 1 LE in positive
-Richtung („nach links“) und um 1 LE in positive  -Richtung („nach oben“).
-Richtung („nach oben“).
 Verschiebung um 1 LE in negative
Verschiebung um 1 LE in negative  -Richtung („nach links“) und um 2 LE in negative
-Richtung („nach links“) und um 2 LE in negative  -Richtung („nach unten“).
-Richtung („nach unten“).
 Verschiebung um 3 LE in positive
Verschiebung um 3 LE in positive  -Richtung („nach oben“) und anschließende Spiegelung an der
-Richtung („nach oben“) und anschließende Spiegelung an der  -Achse.
-Achse.
 Verschiebung um 3 LE in positive
Verschiebung um 3 LE in positive  -Richtung („nach rechts“) und anschließende Spiegelung an der
-Richtung („nach rechts“) und anschließende Spiegelung an der  -Achse.
-Achse.
 Verschiebung um 4 LE in positive
Verschiebung um 4 LE in positive  -Richtung („nach oben“) und um 3 LE in negative
-Richtung („nach oben“) und um 3 LE in negative  -Richtung („nach links“).
-Richtung („nach links“).
a)
b)
c)
d)
e)
f)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Skizze
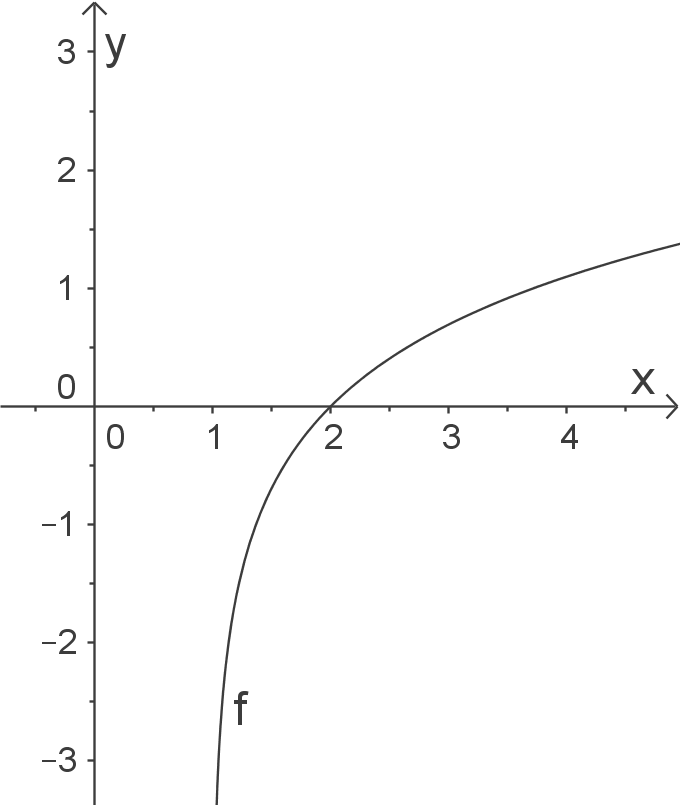
Der Logarithmus ist nur für positive Werte definiert:
b)
Skizze
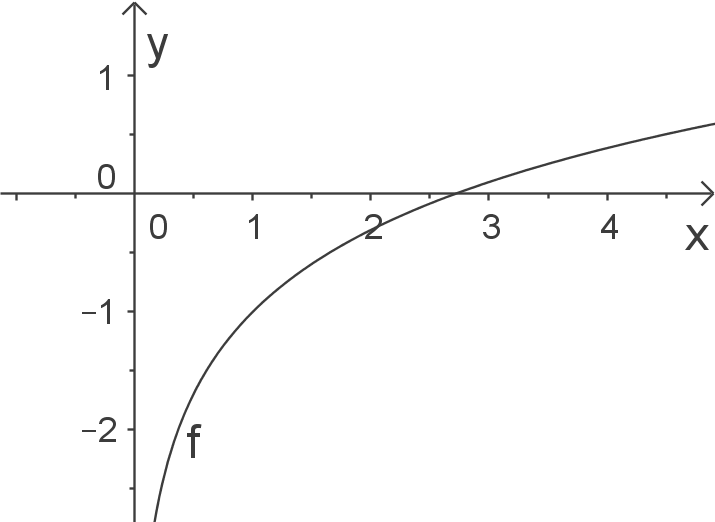
Der Logarithmus ist nur für positive Werte definiert:
c)
Skizze
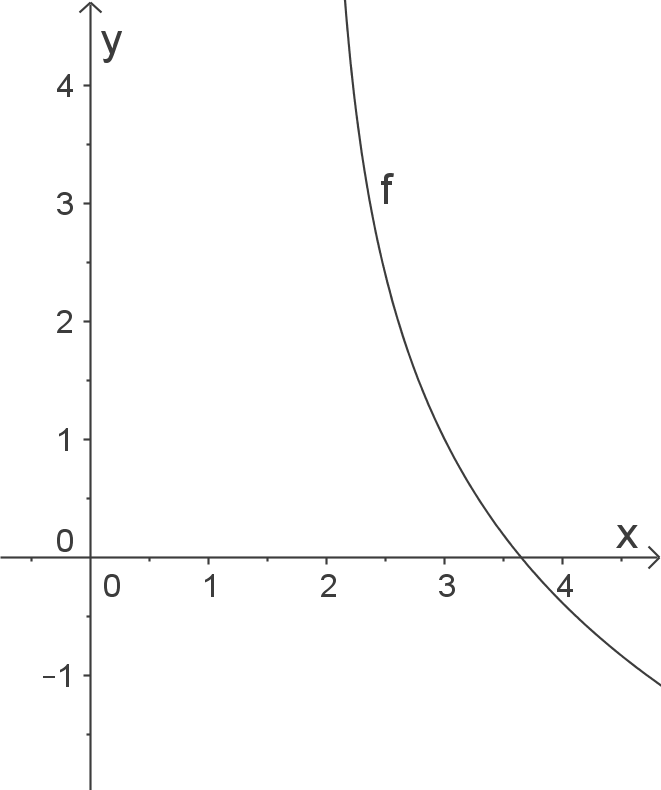
Der Logarithmus ist nur für positive Werte definiert:
d)
Skizze
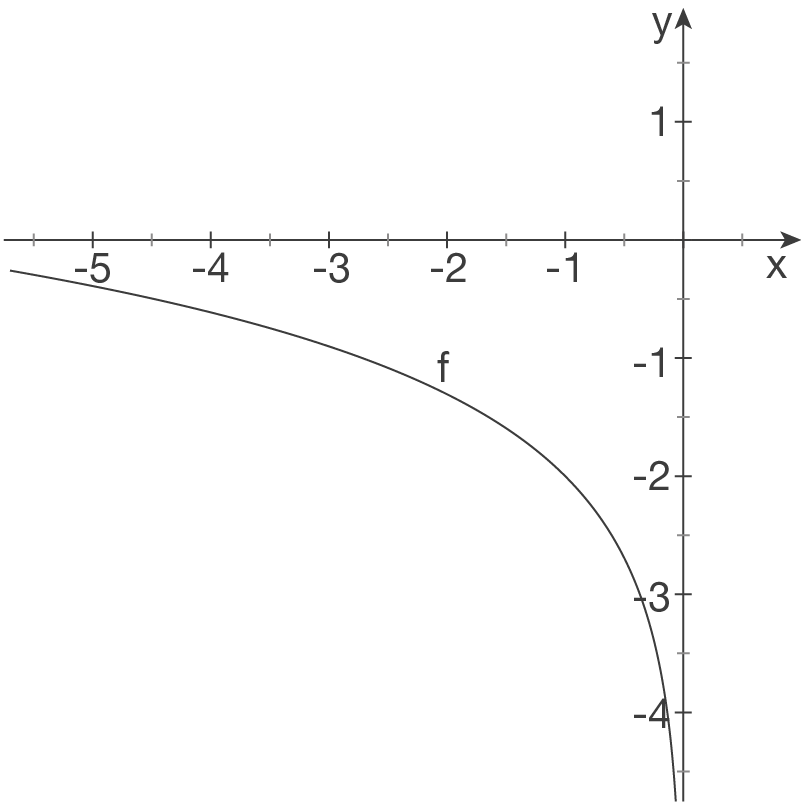
Der Logarithmus ist nur für positive Werte definiert:
e)
Skizze
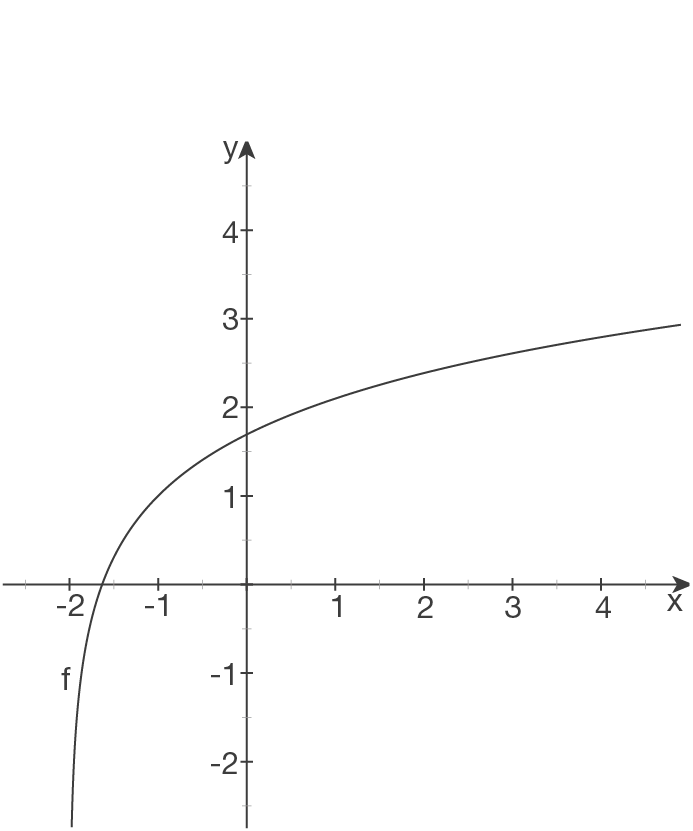
Der Logarithmus ist nur für positive Werte definiert:
f)
Skizze
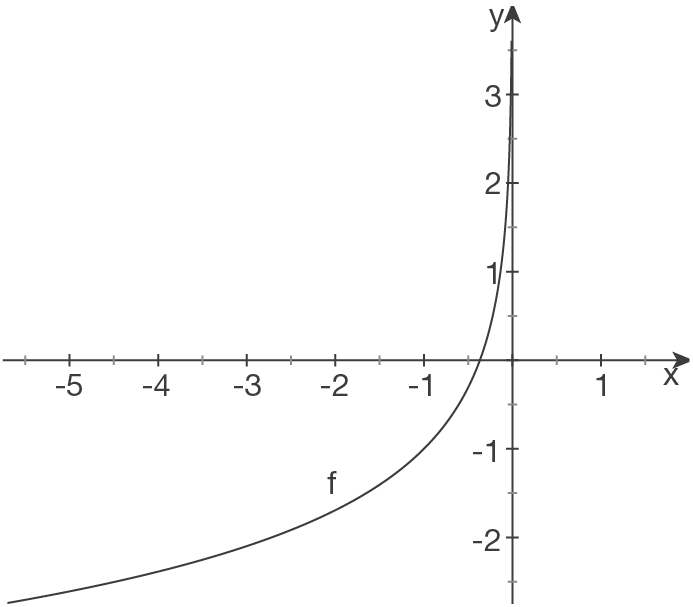
Der Logarithmus ist nur für positive Werte definiert:
2.
a)
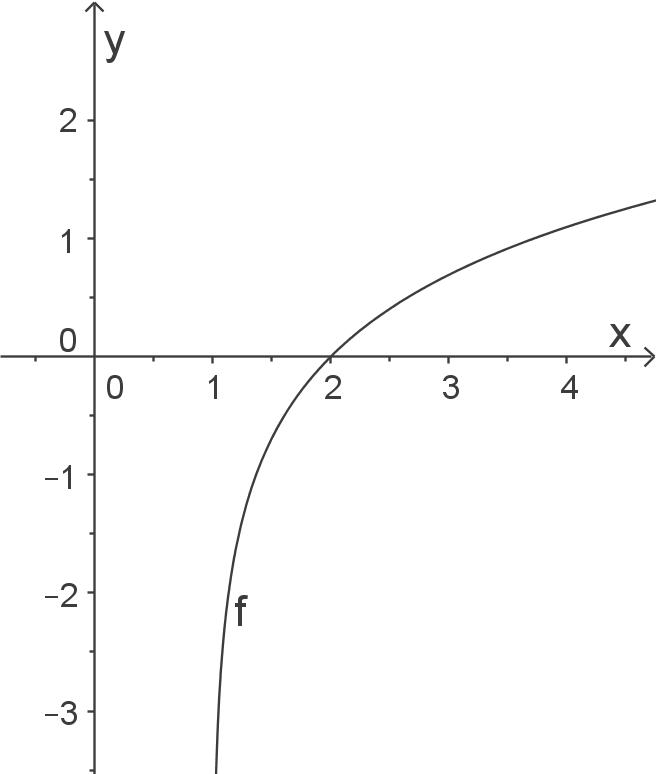
b)
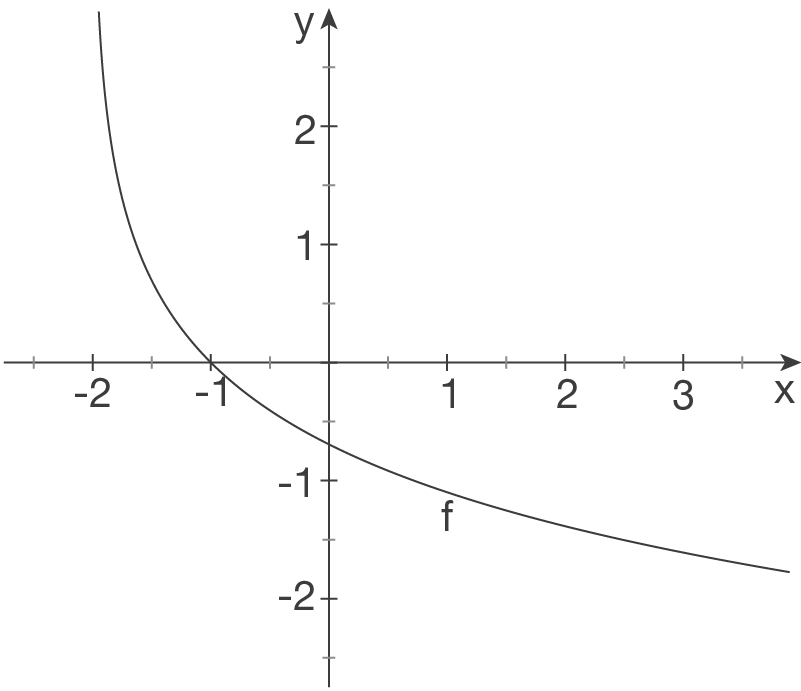
c)
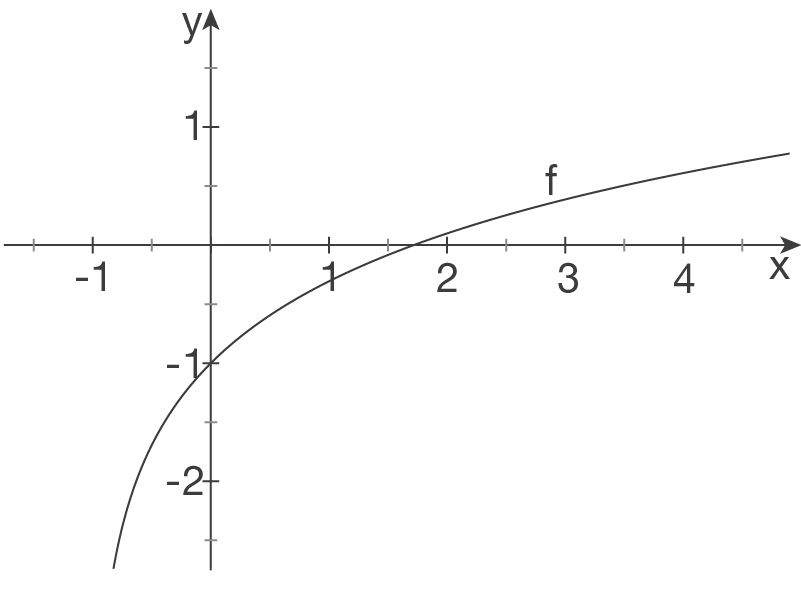
d)
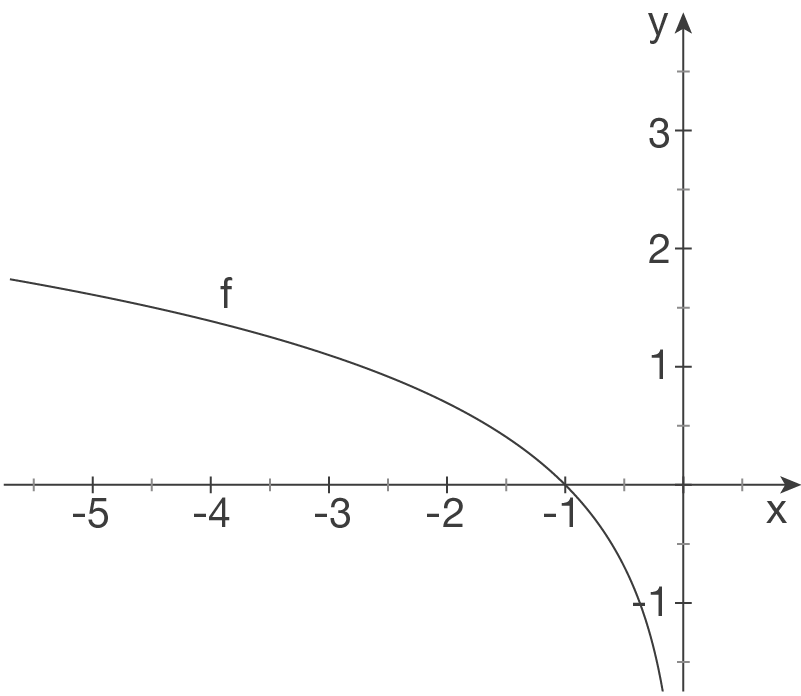
e)
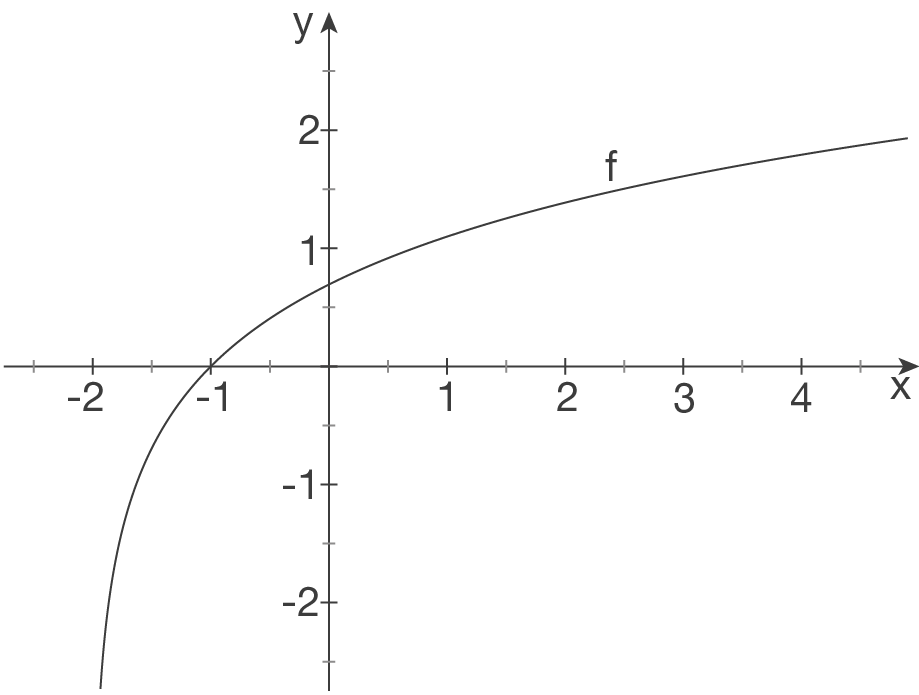
f)
3.
a)
b)
c)
d)
e)
f)