Gebrochenrationale Funktionen
Gebrochenrationale Funktionen besitzen ganzrationale Funktionen im Zähler sowie im Nenner, sind also Funktionen der Form:
Um solche Funktionen zu zeichnen, gehe wie folgt vor:
- bestimme die Nullstellen des Zählers und Nenners
- falls eine Nullstelle
des Zählers und Nenners zusammenfällt, gibt es zwei Möglichkeiten
ist eine hebbare Definitionslücke, d.h. die Funktion ist an dieser Stelle nicht definiert, aber die Funktion kann an dieser Stelle einfach weitergezeichnet werden
- der untere Term der Funktion konvergiert bei
schneller gegen
. Zeichne an dieser Stelle eine senkrechte Asymptote ein
- die restlichen Nullstellen des unteren Term sind ebenfalls senkrechte Asymptoten. Zeichne diese ebenso ein
- zwischen diesen Asymptoten gibt es mindestens ein Maximum, Minimum oder Sattelpunkt. Finde das heraus indem du mithilfe der Quotientenregel die Nullstellen der ersten Ableitung betrachtest und mit der zweiten Ableitung, über Maximum, Minimum oder Sattelpunkt entscheidest
- finde heraus, wie sich die Funktion links und rechts von den Asymptoten verhält, indem du die Funktion von links und rechts gegen die Asymptote annäherst
- zeichne die Teilgraphen zwischen den Asymptoten ein
- um den Bereich vor der ersten und letzten Asymptote zu bestimmen, bestimme die waagrechte Asymptote, indem du die Funktion
gegen
bzw.
laufen lässt
1.
Skizziere die Schaubilder folgender Funktionen und bestimme die Gleichung der Asymptote.




a)
b)
c)
d)
2.
Skizziere das Schaubild der Funktion und beschreibe, wie es aus dem Schaubild der Funktion  bzw.
bzw.  hervorgeht.
hervorgeht.




a)
b)
c)
d)
3.
Verschiebe das Schaubild der angegebenen Funktion wie gefordert und gib die Funktionsgleichung der neuen Funktion an.
 Verschiebung um 2 LE in positive x-Richtung („nach rechts“) und um 1 LE in positive y-Richtung („nach oben“)
Verschiebung um 2 LE in positive x-Richtung („nach rechts“) und um 1 LE in positive y-Richtung („nach oben“)
 Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 2 LE in positive y-Richtung („nach oben“)
Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 2 LE in positive y-Richtung („nach oben“)
 Verschiebung um 1 LE in negative x-Richtung („nach links“) und anschließende Spiegelung an der y-Achse
Verschiebung um 1 LE in negative x-Richtung („nach links“) und anschließende Spiegelung an der y-Achse
 Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Skizze
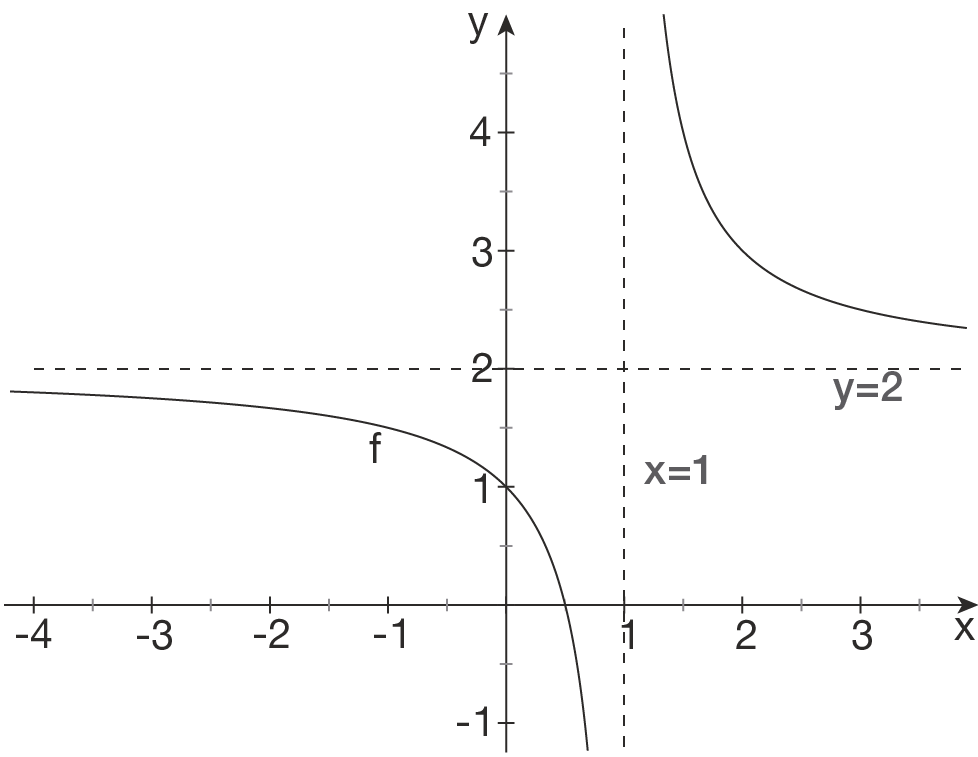
Senkrechte Asymptote - Nennernullstelle
Die Gleichung der senkrechten Asymptote lautet
Waagerechte Asymptote - Grenzwert bestimmen
Die Gleichung der waagerechten Asymptote lautet
b)
Skizze
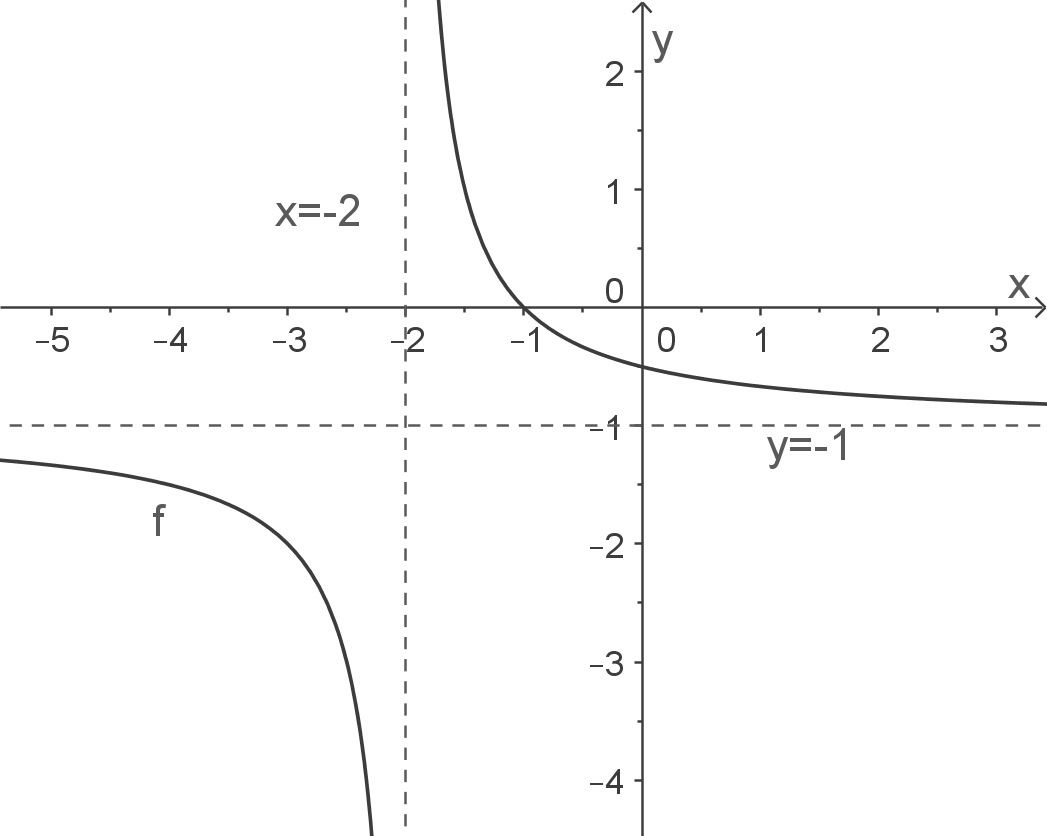
Senkrechte Asymptote - Nennernullstelle
Die Gleichung der senkrechten Asymptote lautet
Waagerechte Asymptote - Grenzwert bestimmen
Die Gleichung der waagerechten Asymptote lautet
c)
Skizze
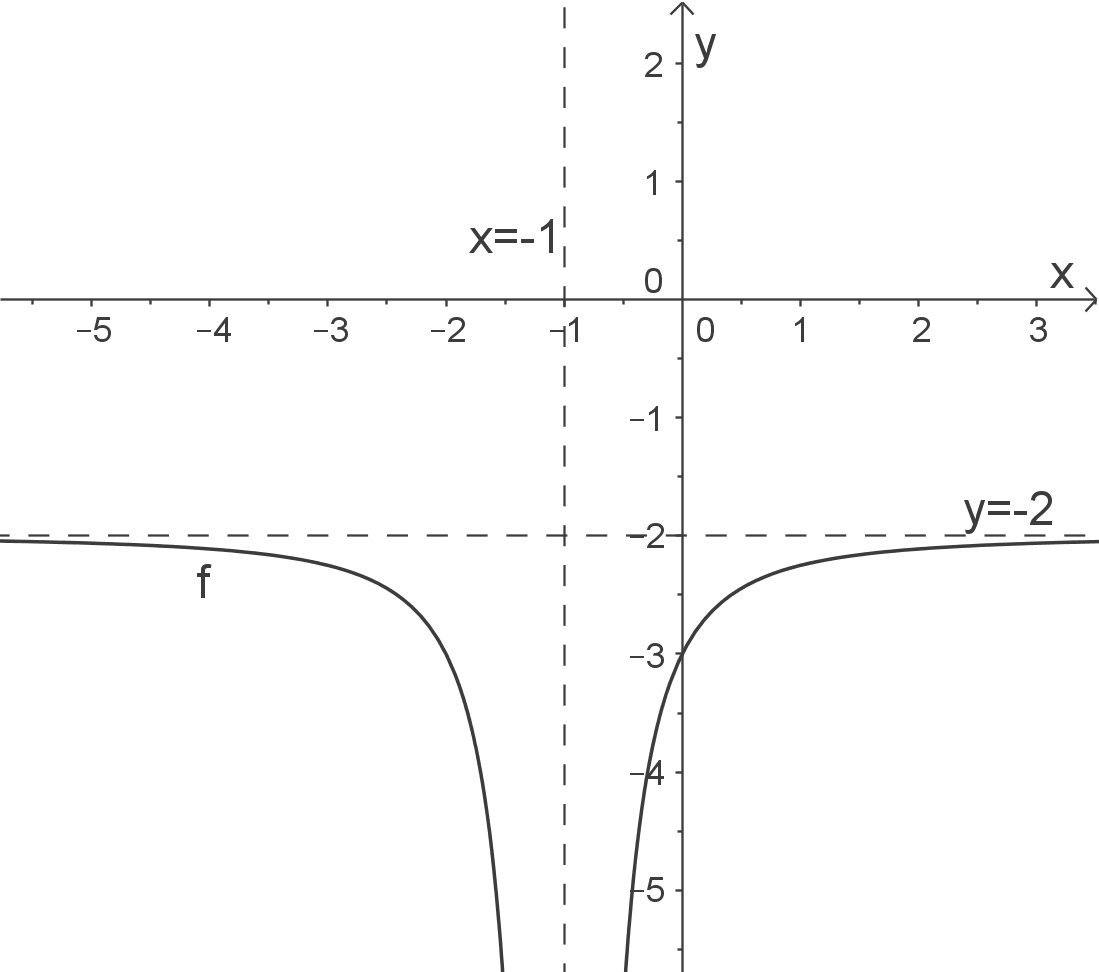
Senkrechte Asymptote - Nennernullstelle
Die Gleichung der senkrechten Asymptote lautet
Waagerechte Asymptote - Grenzwert bestimmen
Die Gleichung der waagerechten Asymptote lautet
d)
Skizze
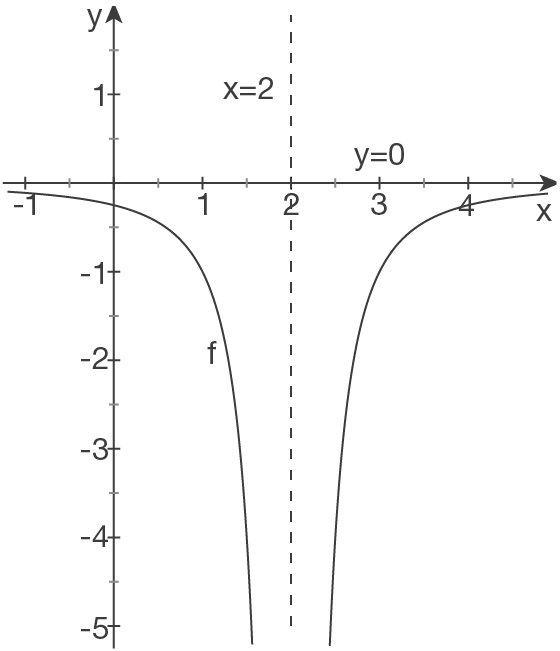
Waagerechte Asymptote - Grenzwert bestimmen
Die Gleichung der waagerechten Asymptote lautet
2.
a)
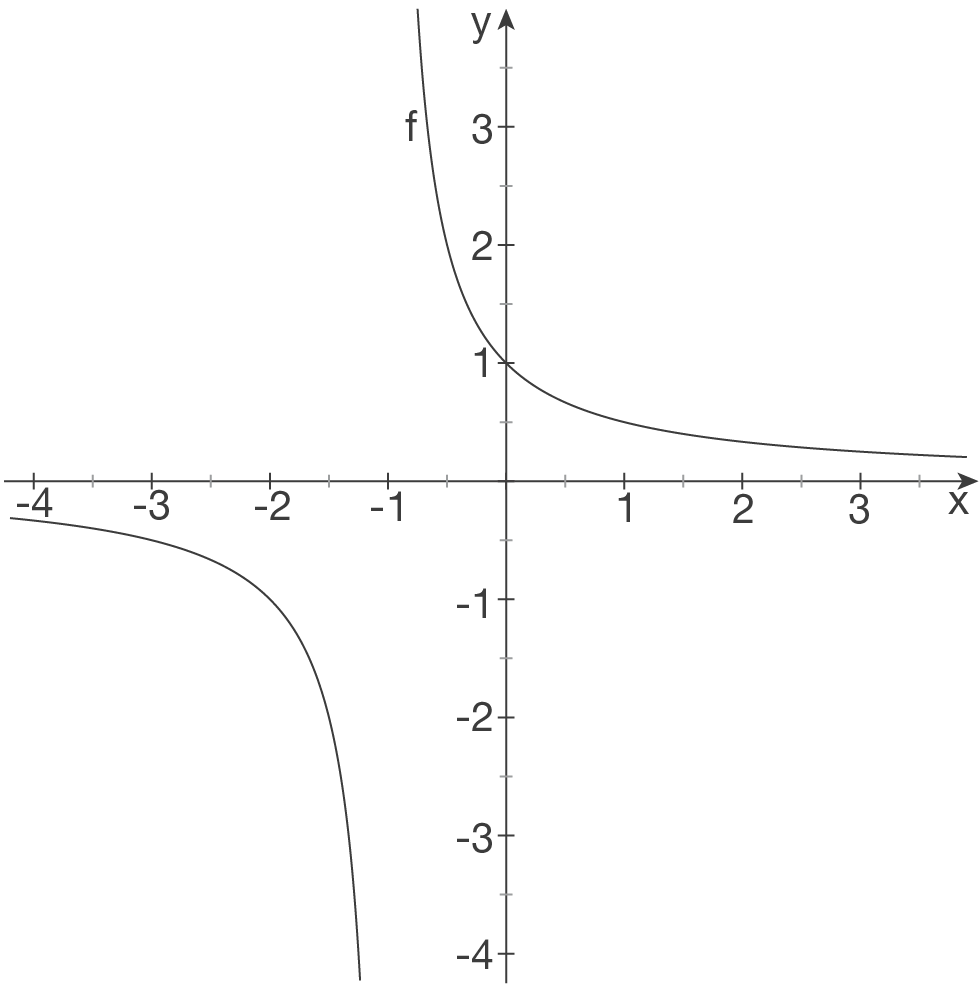
b)
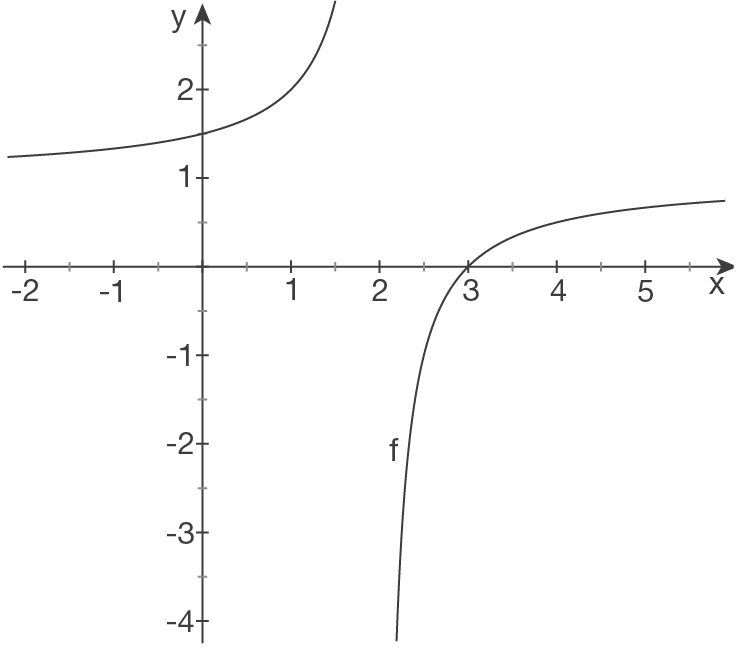
c)
Skizze
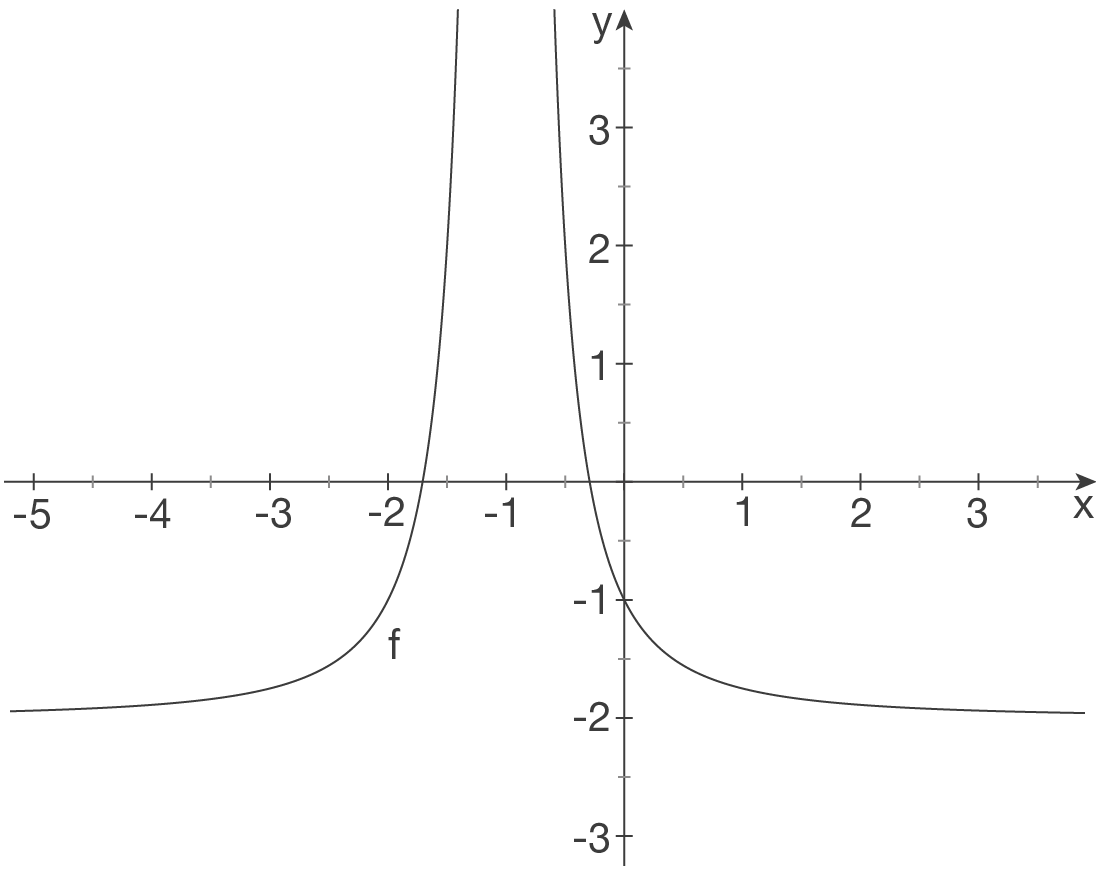 Schaubild herleiten
Schaubild von
Schaubild herleiten
Schaubild von  um 1 LE in negative
um 1 LE in negative  -Richtung („nach links“) und um 2 LE in negative
-Richtung („nach links“) und um 2 LE in negative  -Richtung („nach unten“) verschoben.
-Richtung („nach unten“) verschoben.

d)
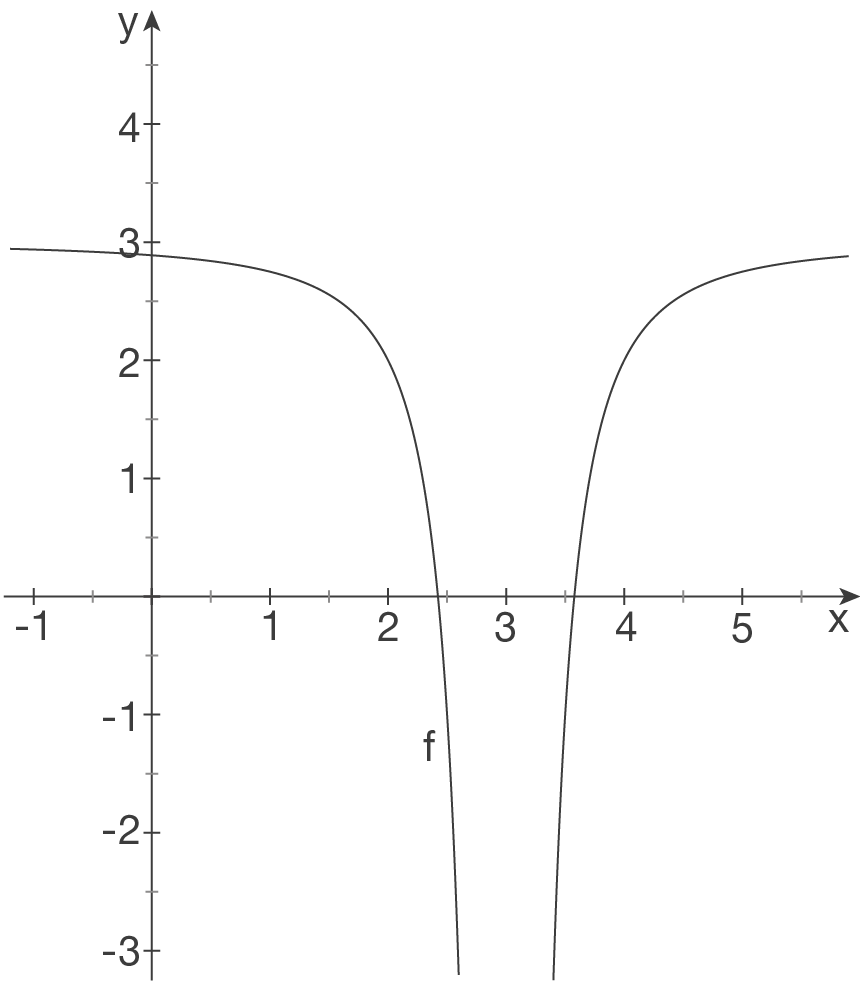
3.
a)
b)
c)
d)