Verflechtungsdiagramm | Gozintograph
Ein Verflechtungsdiagramm (Gozintograph) ist eine alternative Darstellung der Input-Output Tabelle. Dabei werden die einzelnen Zellen der Input-Output Tabelle durch Pfeile dargestellt. Ähnlich einem Übergangsgraphen werden die Pfeile beschriftet, aber nicht mit Wahrscheinlichkeiten, sondern mit Stückzahlen.
Aufgabe: Konstruiere dazu ein Verflechtungsdiagramm.
Lösung:
Wir haben 2 Abteilungen und einen Markt. Somit zeichnen wir diese Bausteine unseres Diagramms ein. Dabei verwenden wir die Kreise für Abteilungen und Kästen für den Markt.
Jetzt wollen wir die Verflechtungen dieser Bausteine einbauen. Diese werden durch die Pfeile dargestellt. Den Inhalt der zugehörigen Zellen tragen wir über die Pfeile ein.
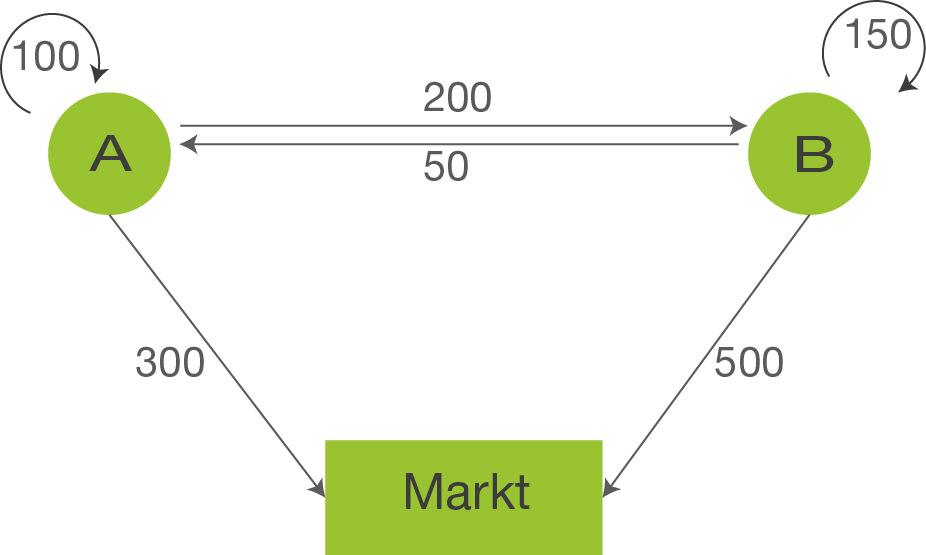
Wir beginnen mit dem Eigenbedarf der Abteilung A und erhalten einen Pfeil der von A auf A zeigt, den zugehörigen Wert lesen wir der Input-Output Tabelle ab und erhalten 100. Analog erhalten wir den Eigenbedarf der Abteilung B, der 150 beträgt.
Weiter gibt die Abteilung A an die Abteilung B 200 Einheiten ab, und Abteilung B an die Abteilung A 50 Einheiten. Schließlich kommen 300 Einheiten von der Abteilung A und 500 Einheiten von der Abteilung B an den Markt, so entstehen die Pfeile von der jeweiligen Abteilung an den Markt. Insgesamt erhalten wir folgendes Verflechtungsdiagramm:
Beispiel
Gegeben ist eine Input-Output Tabelle:| Output\Input | Abteilung A | Abteilung B |
|---|---|---|
| Abteilung A | 100 | 200 |
| Abteilung B | 50 | 150 |
Vollständige Lösung anzeigen
1.
In einem Unternehmen sind die Abteilungen A, B und C nach dem Leontief-Modell miteinander verflochten. Alle Lieferungen untereinander, sowie an den Markt sind in Geldeinheiten angegeben. Die Verflechtung wird dabei durch folgende Input-Output-Tabelle dargestellt.
| Input Output | Abteilung |
Abteilung |
| Abteilung |
320 | 60 |
| Abteilung |
30 | 150 |
| Abteilung |
40 | 200 |
a)
Zeichne das Verflechtungsdiagramm zu der Input-Output-Tabelle und gib Produktions- und Marktabgabevektor an.
b)
Interpretiere das Verflechtungsdiagramm im Sachzusammenhang.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Verflechtungsdiagramm zeichnen
Ein Verflechtungsdiagramm ist die graphische Darstellung einer Input-Output-Tabelle. Daher stellt es ebenfalls die einzelnen Abteilungen und deren Verflechtungen dar. In den Zeilen einer Input-Output-Tabelle kannst du ablesen, wie die Produktionseinheiten der jeweiligen Abteilung verwendet werden, das heißt, wie viele Produktionseinheiten an die jeweils anderen Abteilungen und den Markt abgegeben werden und wie viele als Eigenbedarf zur weiteren Produktion in der eigenen Abteilung behalten werden.
In einem Verflechtungsdiagramm wird dies durch Pfeile dargestellt, die mit der Menge der abgegebenen Produktionseinheiten an die jeweilige andere Abteilung beschriftet sind.
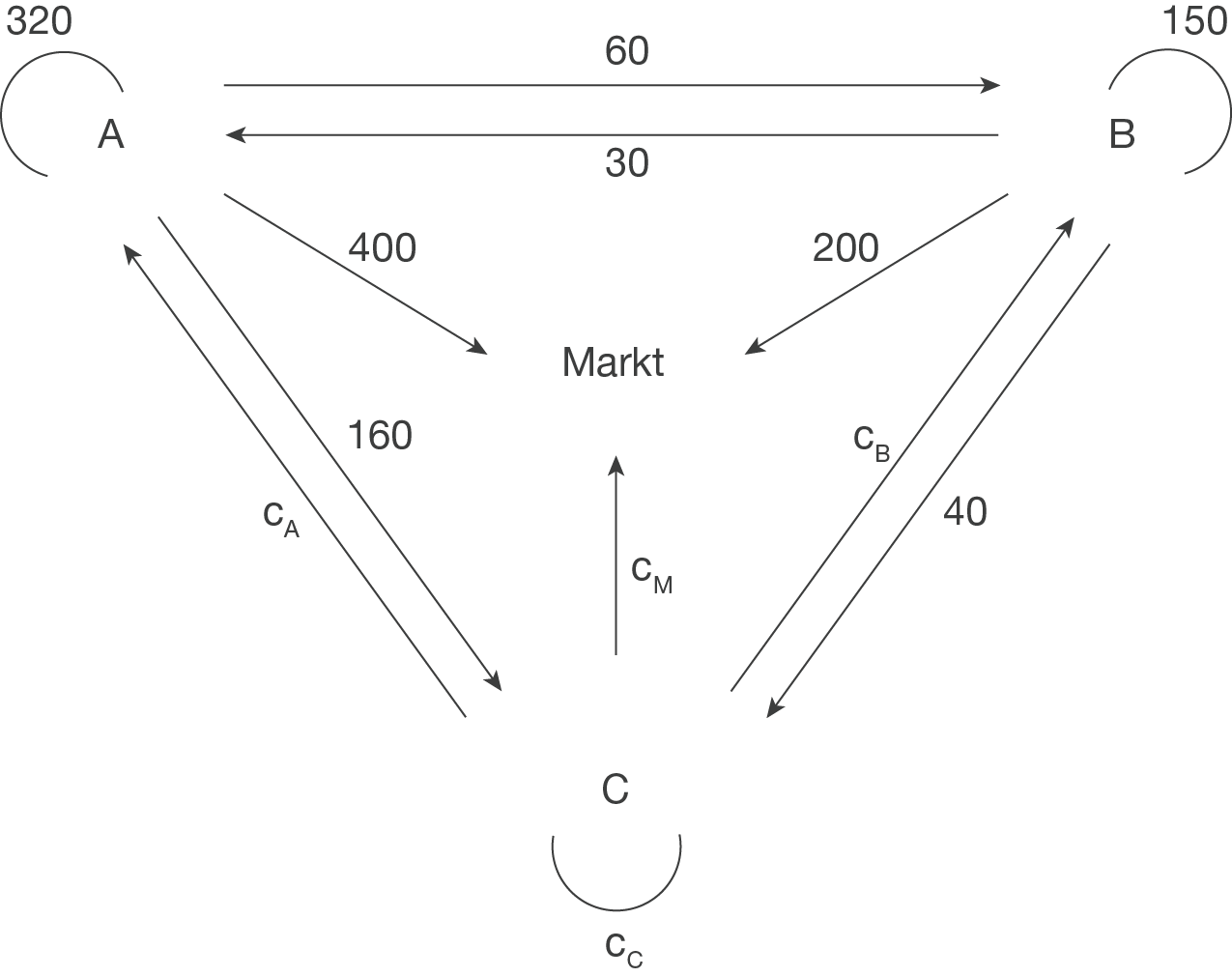
Ein Verflechtungsdiagramm hat folgende Form:
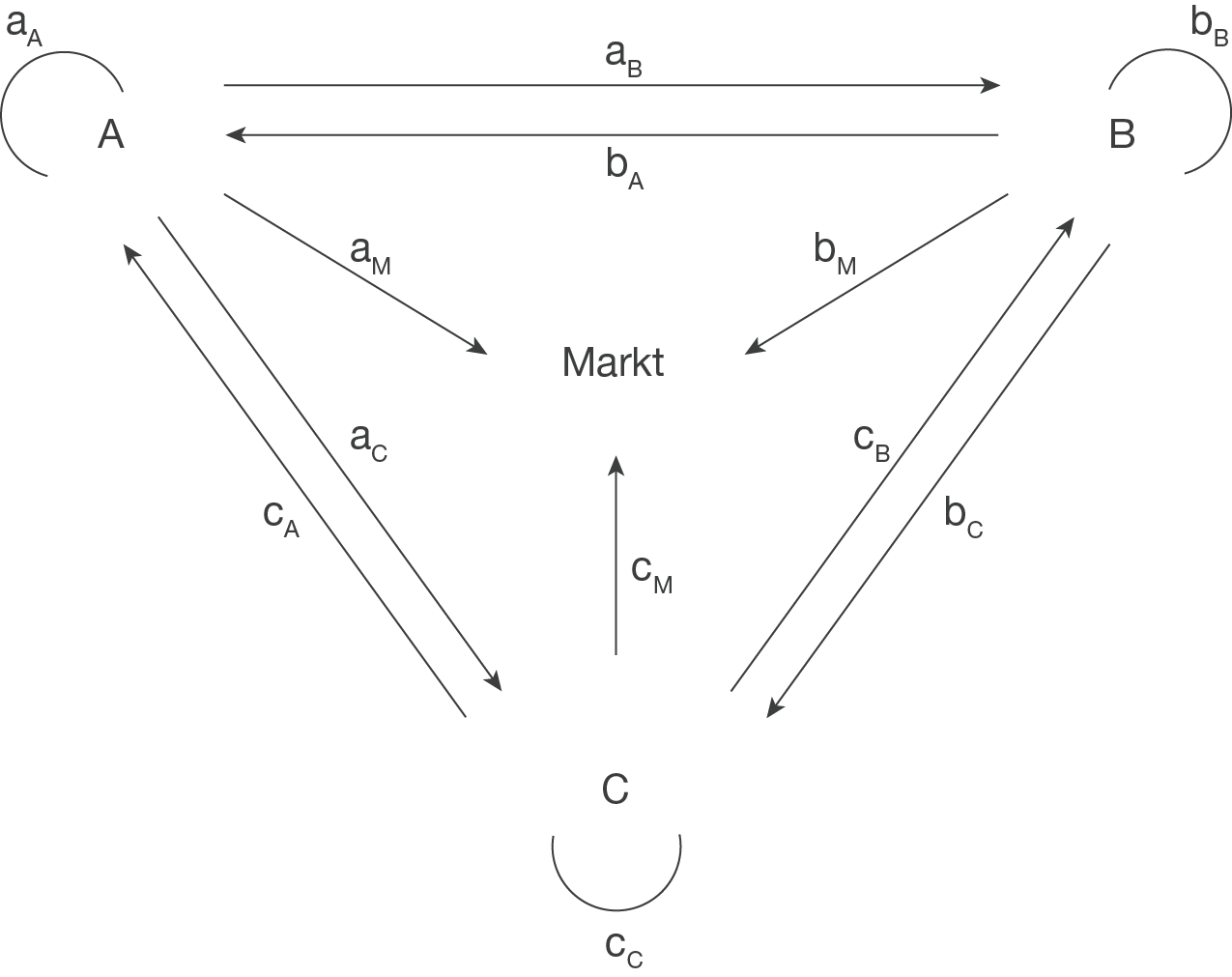Dabei bezeichnet beispielsweise 
die Menge der Produktionseinheiten, die Abteilung A an Abteilung C abgibt.
Du siehst, dass die Abteilungen bereits eingetragen sind. Du musst nun also noch die Beschriftungen der Pfeile aus der Tabelle ablesen.
1. Schritt: Abteilung A
Wir beginnen hier nun mit den Pfeilen die von Abteilung A abgehen, also allen Produktionseinheiten, die Abteilung A abgibt bzw. selbst behält. Wir benötigen also die erste Zeile der Tabelle.
Daraus kannst du ablesen, dass Abteilung A 320 Einheiten selbst behält, 60 Einheiten an Abteilung B, 160 Einheiten an Abteilung C und 400 Einheiten an den Markt abgibt. Daraus ergibt sich:
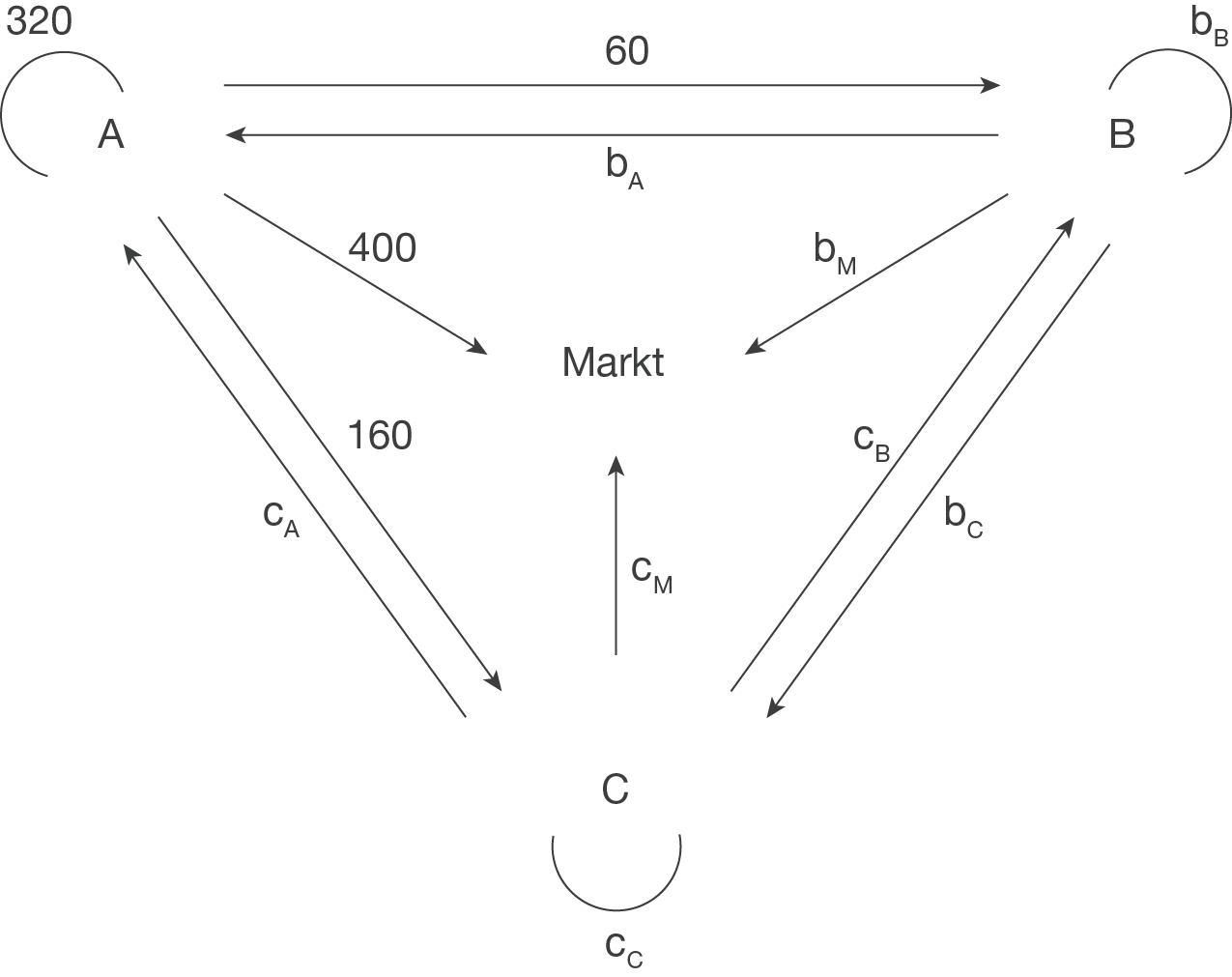2. Schritt: Abteilung B
Aus der zweiten Zeile der Tabelle kannst du ablesen, wie viele Produktionseinheiten Abteilung B abgibt. Daraus ergibt sich dann:
3. Schritt: Abteilung C
Lies hier die Abgaben der Abteilung C aus der dritten Zeile ab:
Marktabgabevektor bestimmen
Der Marktabgabevektor gibt an, wie viele Produktionseinheiten die einzelnen Abteilungen jeweils an den Markt abgeben. Seine Einträge sind also genau die Einträge der letzten Spalte in der Tabelle bzw. alle Pfeile, die im Verflechtungsdiagramm zu „Markt“ zeigen.
Daher hat er folgende Form:
Die benötigten Werte kennst du bereits, daher ergibt sich der Marktabgabevektor mit:
Produktionsvektor
Der Produktionsvektor, gibt an, wie viele Produktionseinheiten in jeder Abteilung insgesamt produziert werden.
Er hat demnach folgende Form:
In unserem Fall ergibt sich also der folgende Produktionsvektor:
=
b)
Verflechtungsdiagramm im Sachzusammenhang interpretieren
Du sollst erklären, welchen Sachverhalt das Verflechtungsdiagramm darstellt. In Aufgabenteil a) haben wir dies bereits im Ansatz getan. Du weißt daher, wofür die einzelnen Pfeile stehen und was sie im Sachzusammenhang bedeuten. Wir gehen bei der Interpretation nun wieder nacheinander jede der Abteilungen A, B und C durch.
Abteilung A:
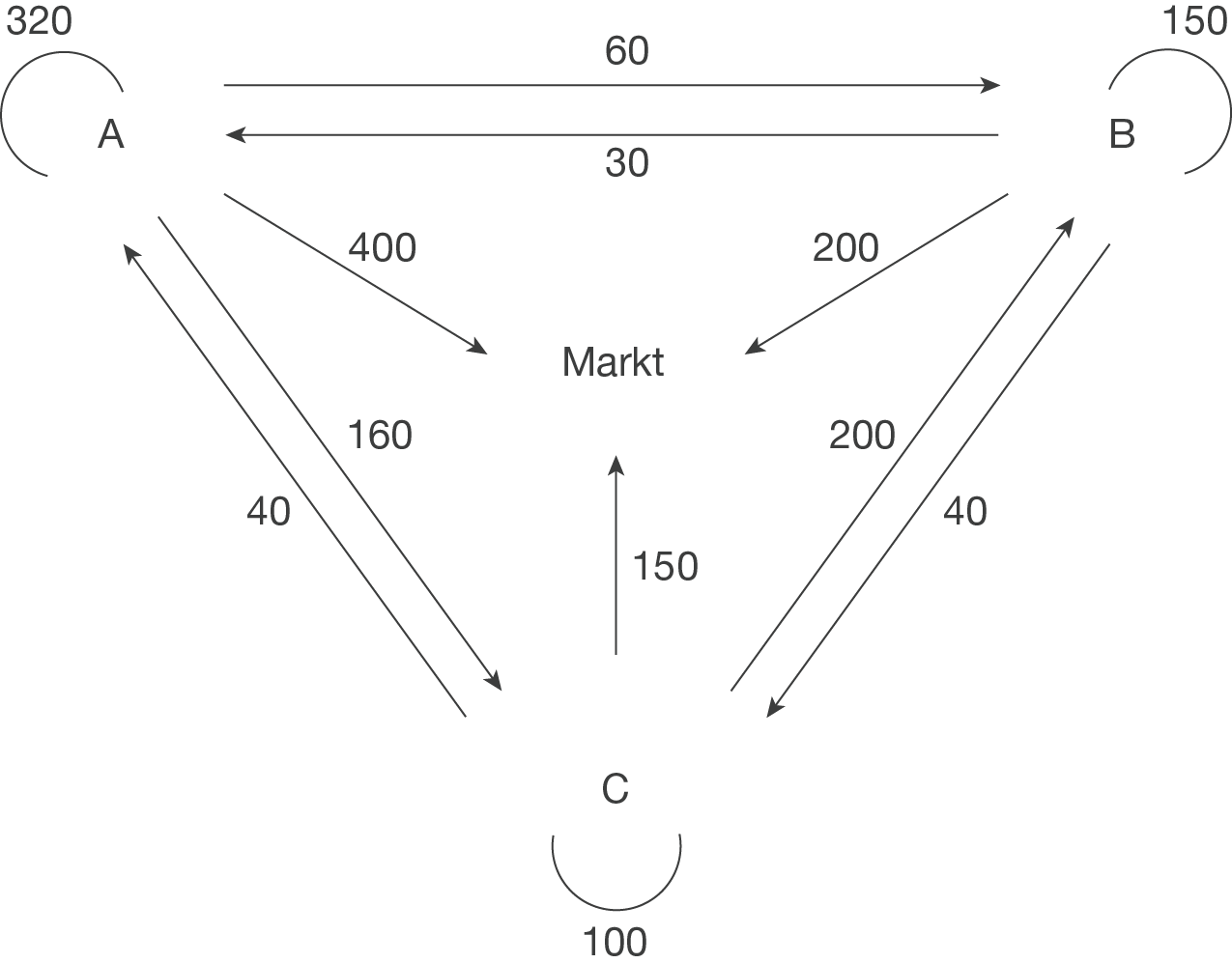
Aus dem Verflechtungsdiagramm kannst du ablesen, dass die Abteilung A des Unternehmens 320 Geldeinheiten (GE) für den Eigenbedarf behält, 60 GE an Abteilung B und 160 GE an Abteilung C abgibt. Außerdem gehen 400 GE in den Markt. Insgesamt produziert Abteilung A also 940 GE.
Abteilung B:
Abteilung B gibt 30 GE an Abteilung A ab und behält 150 GE zum Eigenbedarf. Außerdem gibt Abteilung B 40 GE an Abteilung C und 200 GE an den Markt ab. Die Abteilung B produziert also insgesamt 420 GE.