Übergangsmatrix

Die Einträge einer Übergangsmatrix geben die Wahrscheinlichkeiten eines Übergangs von einem Zustand zu einem anderen Zustand an.

Die Zeilen und Spalten der Übergangsmatrix werden beschriftet, die Spalten geben den Ausgangszustand an und die Zeilen den Zustand nach dem Übergang.

Die Einträge der Diagonalen geben die Wahrscheinlichkeit an, dass kein Übergang in einen anderen Zustand stattfindet.

Die Summer der Spalteneinträge ist immer $1$ .

$a_{11}+a_{21}+a_{31} = 1$

$a_{12}+a_{22}+a_{32} = 1$

$a_{13}+a_{23}+a_{33} = 1$

Vollständige Tabelle anzeigen

Beispiel

Der Markt von Tablet-PCs wird im wesentlichen von drei Herstellern A, S und M beherrscht.

Nach einem Jahr bleiben $65\%$ der Kunden von A dem Hersteller treu, $15\%$ der Kunden wechseln zum Hersteller M und $20\%$ wechseln zum Hersteller S.

Dagegen bleiben $40\%$ dem Hersteller S treu, $20\%$ wechseln zu M und $40\%$ wechseln zum Hersteller A.

Dem Hersteller M bleiben $50\%$ treu, $30\%$ wechseln zum Hersteller A und $20\%$ wechseln zum Hersteller S.

Bilde die Übergangsmatrix M.

		von:	$A$	$S$	$M$
	$A$		$\begin{pmatrix}0,65&0,4&0,3\\[2pt]0,2&0,4&0,2\\[2pt]0,15&0,2&0,5\end{pmatrix}$
nach:	$S$	$M=$
	$M$

Stelle die im Text beschriebenen Übergänge in einer Übergangsmatrix dar.

Ein Reisebüro bietet Reisen per Bahn, per Schiff und per Flug an. Über die letzten Jahre hinweg konnte das Reisebüro folgende Erfahrungswerte ermitteln:

Von den Reisenden, die per Flug gereist sind, wählen $\small{80\%}$ auch bei ihrer nächsten Reise das Flugzeug. $\small{20\%}$ steigen auf die Bahn um.

Von den Reisenden, die per Bahn gereist sind, wählen $\small{50\%}$ bei ihrer nächsten Reise wieder die Bahn, $\small{30\%}$ steigen auf das Flugzeug und $\small{20\%}$ steigen auf das Schiff um.

Von den Reisenden, die per Schiff gereist sind, wählen $\small{60\%}$ wieder das Schiff. Die anderen $\small{40\%}$ steigen bei ihrer nächsten Reise auf das Flugzeug um.

Ein Fortbildungsangebot besteht aus drei unterschiedlichen Seminaren, die die Teilnehmer nacheinander besuchen und auch bestehen müssen. Wenn ein Teilnehmer ein Seminar nicht besteht, so darf er es einmal wiederholen; besteht er es ein zweites Mal nicht, so muss er die Fortbildung abbrechen.

Darüber hinaus gibt es auch Teilnehmer, die die Fortbildung aus Zeitgründen oder anderen persönlichen Motiven abbrechen bzw. auf einen späteren Zeitpunkt verschieben.

Über die letzten Jahre ließen sich folgende Erfahrungswerte ermitteln:

Von den Teilnehmern an Seminar 1 nehmen im Anschluss $\small{80\%}$ an Seminar 2 Teil und $\small{10\%}$ müssen Seminar 1 wiederholen. Die anderen scheiden aus dem Programm aus.

Von den Teilnehmern an Seminar 2 nehmen im Anschluss $\small{70\%}$ an Seminar 3 Teil; $\small{15\%}$ müssen Seminar 2 wiederholen. Die restlichen scheiden aus dem Programm aus.

Von den Teilnehmern an Seminar 3 schließlich bestehen $\small{90\%}$ . $\small{5\%}$ müssen Seminar 3 wiederholen, die restlichen $\small{5\%}$ scheiden aus dem Programm aus.

Eine Kontaktbörse im Internet bietet kostenpflichtige Mitgliedschaften für 3 Monate, 6 Monate und 12 Monate an. Nach Ablauf der Mitgliedschaft können die Nutzer sich für eine weitere Mitgliedschaft auf 3, 6 oder 12 Monate entscheiden, oder das Angebot verlassen.

Im Rahmen einer Werbekampagne bietet die Kontaktbörse für die bestehenden Nutzer die Möglichkeit an, neue Nutzer für eine Mitgliedschaft auf 3, 6, oder 12 Monate zu werben.

Die Unternehmensleitung geht von folgendem Kundenverhalten aus:

Von den Nutzern, die eine Mitgliedschaft auf 3 Monate gebucht haben, entscheiden sich im Anschluss $\small{50\%}$ für eine weitere Mitgliedschaft auf 3 Monate und $\small{20\%}$ entscheiden sich für eine Mitgliedschaft auf 6 Monate. Außerdem werben $\small{10\%}$ dieser Nutzer je ein Mitglied für eine Mitgliedschaft auf 3 Monate.

Von den Nutzern, die eine Mitgliedschaft auf 6 Monate gebucht haben, entscheiden sich im Anschluss $\small{10\%}$ für eine Mitgliedschaft auf 3 Monate, $\small{50\%}$ für eine weitere Mitgliedschaft auf 6 Monate und $\small{10\%}$ entscheiden sich für eine Mitgliedschaft auf 12 Monate. Außerdem werben $\small{20\%}$ dieser Nutzer je ein Mitglied für eine Mitgliedschaft auf 3 Monate und $\small{15\%}$ dieser Nutzer je ein Mitglied für eine Mitgliedschaft auf 6 Monate an.

Von den Nutzern, die eine Mitgliedschaft auf 12 Monate gebucht haben, entscheiden sich im Anschluss $\small{80\%}$ für weitere Mitgliedschaft auf 12 Monate. Außerdem werben $\small{30\%}$ dieser Nutzer je ein Mitglied für eine Mitgliedschaft auf 6 Monate und $\small{5\%}$ dieser Nutzer je ein Mitglied für eine Mitgliedschaft auf 12 Monate an.

In der Kantine einer Firma werden täglich drei Gerichte angeboten: Essen 1 (E1), Essen 2 (E2), sowie ein vegetarisches Menü (V).

Einige Stammkunden wählen am nächsten Mittag jeweils das gleiche Gericht, andere entscheiden sich für ein anderes. Das Wahlverhalten der Stammkunden der Kantine ist in folgendem Übergangsgraphen (Übergangsdiagramm) dargestellt:

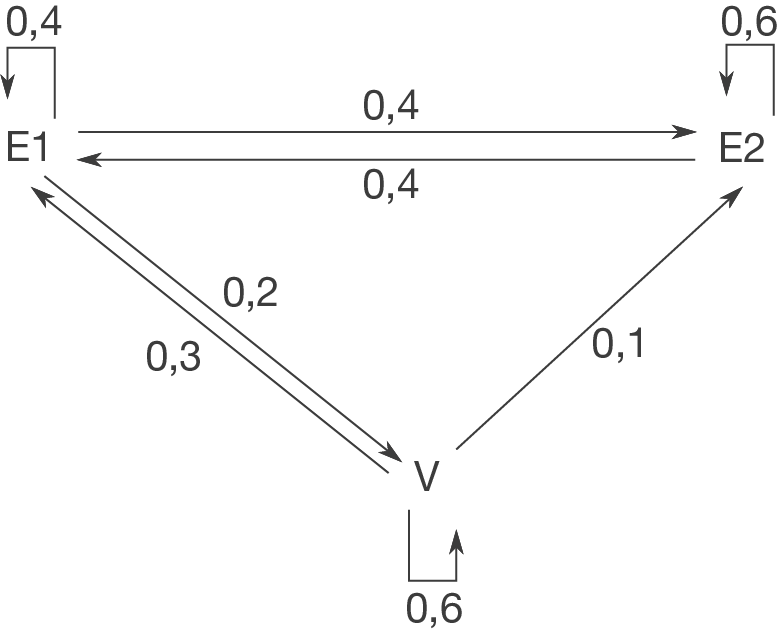Diagramm mit Pfeilen und Werten zur Darstellung von Beziehungen zwischen E1, E2 und V.

Stelle aus dem Übergangsgraphen eine Übergangsmatrix auf. Wie verändert sich diese, wenn $\small{40\%}$ der Leute die das Essen $E1$ gewählt haben vegetarisch essen? Die Anzahl der Stammkunden bleibt konstant.

Eine Firma hat die drei Produktionsstandorte $A$ , $B$ und $C$ . Je nach Bedarf werden die Mitarbeiter in den unterschiedlichen Werken eingesetzt.

Dies beschreibt die folgende Matrix:

		von:	$A$	$B$	$C$
	$A$		$\begin{pmatrix}0,1&0,2&0,7\\[2pt]0,8&0,5&0,2\\[2pt]0,1&0,3&0,1\end{pmatrix}$
nach:	$B$	$M=$
	$C$

Beschreibe was der Eintrag in der zweiten Spalte, dritte Zeile aussagt.

Inwiefern unterscheidet sich folgende Matrix von der in Teiaufgabe a)? Beachte dabei die Summe der Spalteneinträge.

		von:	$A$	$B$	$C$
	$A$		$\begin{pmatrix}0&0&0,4\\[2pt]0,75&0&0\\[2pt]0,8&0,8&0,8\end{pmatrix}$
nach:	$B$	$M=$
	$C$

In einem Reisebüro wird analysiert, wieviele Kunden einen Urlaub in einem Hotel $H$ , einer Ferienwohnung $F$ oder in einer Pension $P$ buchen. Im Jahr $2012$ konnte folgende Übergangsmatrix ermittelt werden:

		von:	$H$	$F$	$P$
	$H$		$\begin{pmatrix}0,75&0,2&0,57\\[2pt]0,1&0,6&0,28\\[2pt]0,15&0,2&0,15\end{pmatrix}$
nach:	$F$	$A=$
	$P$

Im folgenden Jahr hast du eine veränderte Matrix gegeben:

		von:	$H$	$F$	$P$
	$H$		$\begin{pmatrix}0,8&0,2&0,6\\[2pt]0,1&0,6&0,3\\[2pt]0,1&0,2&0,1\end{pmatrix}$
nach:	$F$	$B=$
	$P$

Gib drei Veränderungen der Verteilung gegenüber dem Vorjahr an.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Wir kürzen die Bahn mit $B$ , das Schiff mit $S$ und den Flug mit $F$ ab. Um die Übergangsmatrix zu bestimmen, kannst du den Übergangsgraph zur Hilfe nehmen. Tipp: Wenn du das Aufgabenblatt zu dem Thema Übergangsgraphen bearbeitet hast, hast du die Übergangsgraphen in Aufgabe 2b) schon gebildet.

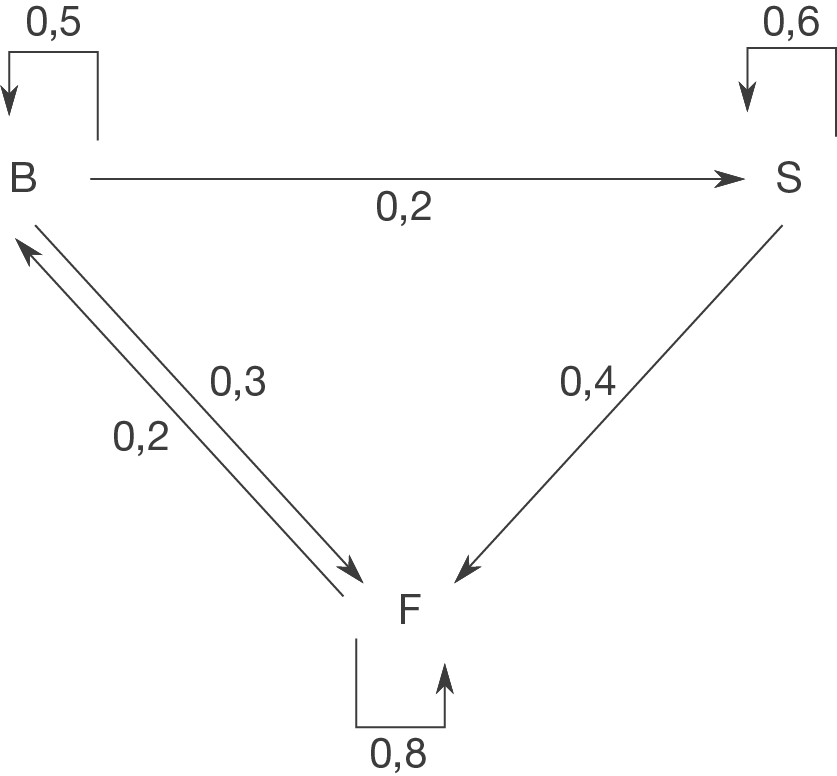Diagramm mit Pfeilen und Zahlen, das verschiedene Kräfte und ihre Richtungen darstellt.

Die Übergangsmatrix lautet demnach:

		von:	$B$	$S$	$F$
	$B$		$\begin{pmatrix}0,5&0&0,2\\[2pt]0,2&0,6&0\\[2pt]0,3&0,4&0,8\end{pmatrix}$
nach:	$S$	$A=$
	$F$

Wir kürzen die drei Seminare mit $S1$ , $S2$ und $S3$ ab. Um die Übergangsmatrix zu bestimmen, kannst du den Übergangsgraph zur Hilfe nehmen. Tipp: Wenn du das Aufgabenblatt zu dem Thema Übergangsgraphen bearbeitet hast, hast du die Übergangsgraphen in Aufgabe 2c) schon gebildet.

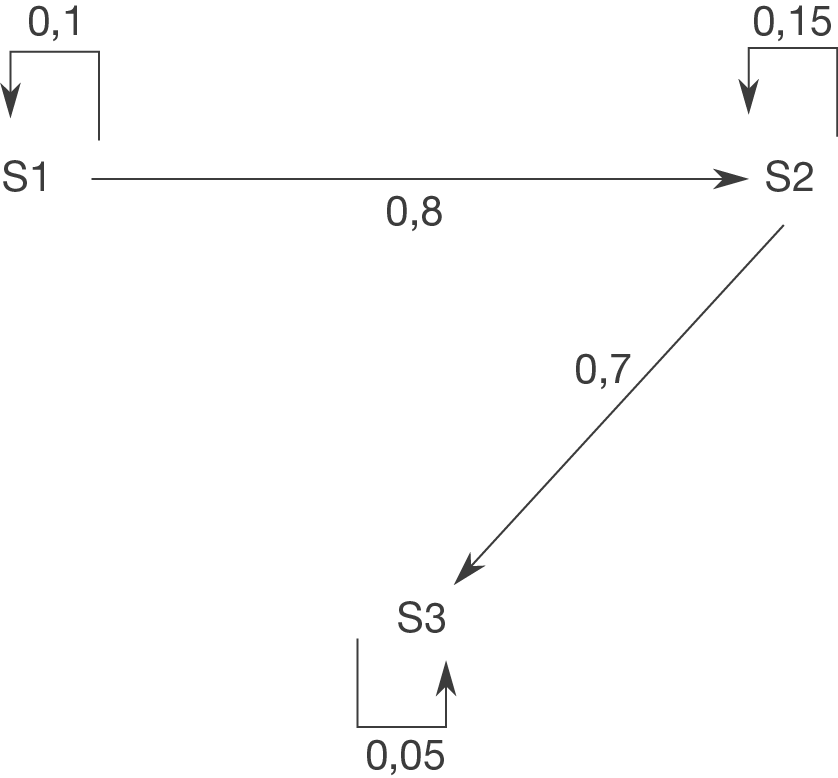Diagramm mit Zuständen S1, S2 und S3 sowie Übergangswahrscheinlichkeiten zwischen den Zuständen.

Die Übergangsmatrix lautet demnach:

		von:	$S1$	$S2$	$S3$
	$S1$		$\begin{pmatrix}0,1&0&0\\[2pt]0,8&0,15&0\\[2pt]0&0,7&0,05\end{pmatrix}$
nach:	$S2$	$A=$
	$S3$

Wir kürzen die drei Laufzeiten mit $M3$ , $M6$ und $M12$ ab. Um die Übergangsmatrix zu bestimmen, kannst du den Übergangsgraph zur Hilfe nehmen. Tipp: Wenn du das Aufgabenblatt zu dem Thema Übergangsgraphen bearbeitet hast, hast du die Übergangsgraphen in Aufgabe 2d) schon gebildet.

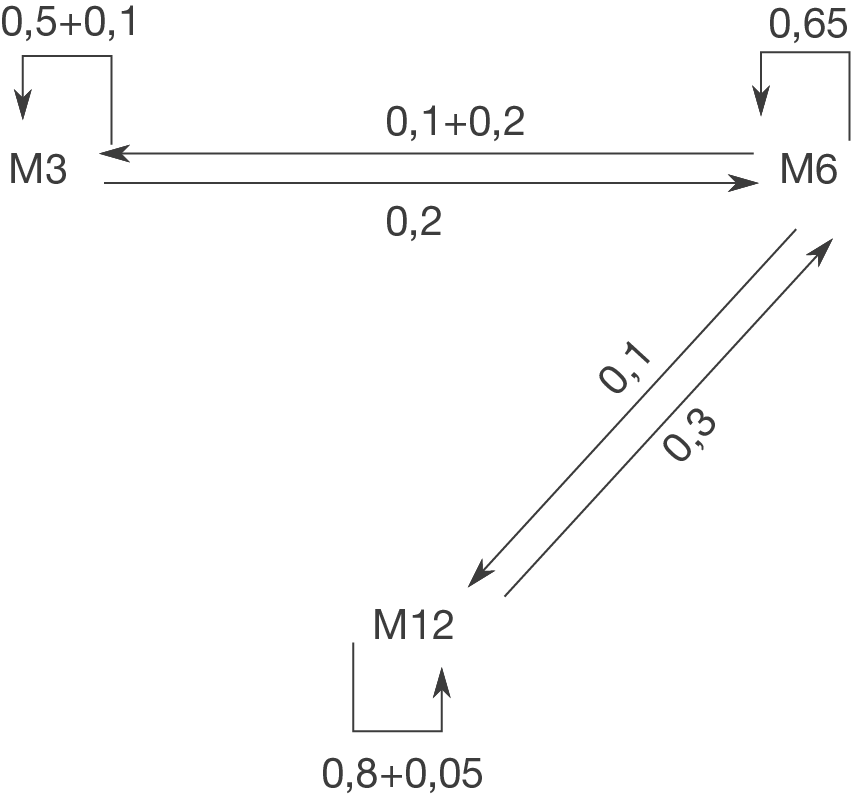
Diagramm mit verschiedenen Werten und Verbindungen zwischen M3, M6 und M12.

Die Übergangsmatrix lautet demnach:

		von:	$M3$	$M6$	$M12$
	$M3$		$\begin{pmatrix}0,6&0,3&0\\[2pt]0,2&0,65&0,3\\[2pt]0&0,1&0,85\end{pmatrix}$
nach:	$M6$	$A=$
	$M12$

Die Übergangsmatrix lautet:

		von:	$E1$	$E2$	$V$
	$E1$		$\begin{pmatrix}0,4&0,4&0,3\\[2pt]0,4&0,6&0,1\\[2pt]0,2&0&0,6\end{pmatrix}$
nach:	$E2$	$A=$
	$V$

Wählen nun $\small{40\%}$ der Stammkunden, die das Essen $E1$ gewählt haben, das vegetarische Essen, so ändert sich der Übergang von $E1$ nach $V$ . Da die Anzahl der Stammkunden gleich bleibt, wählen dementsprechend weniger Menschen wieder das Essen $E1$ . Bisher haben $\small{40\%}$ der Gäste wiederholt das Essen $E1$ gewählt. $\small{40\%}$ von $\small{0,4}$ entsprechen $\small{0,16}$ . Das heißt, es essen nur noch $\small{24\%}$ der Stammkunden wiederholt das Essen $E1$ . Dementsprechend erhöht sich die Zahl bei dem Übergang von Essen $E1$ zu dem vegetarischen Essen $V$ um $\small{0,16}$ .

Die Übergangsmatrix lautet dann:

		von:	$E1$	$E2$	$V$
	$E1$		$\begin{pmatrix}0,24&0,4&0,3\\[2pt]0,4&0,6&0,1\\[2pt]0,36&0&0,6\end{pmatrix}$
nach:	$E2$	$A=$
	$V$

Der Eintrag in der zweiten Spalte, dritte Zeile beschreibt den Übergang von Werk $B$ zu Werk $C$ . Er beträgt $\small{0,3}$ . Das bedeutet, dass $\small{30\%}$ der Mitarbeiter von dem Werk $B$ zu dem Werk $C$ wechseln.

Der Unterschied zwischen den zwei Matrizen besteht darin, dass die Summe der Spalteneinträge bei der Teilaufgabe a) immer $\small{1}$ ergibt und bei Aufgabe b) nicht.

Beträgt die Summe $\small{1}$ heißt das, dass die Summe der Mitarbeiter immer gleich bleibt. Es werden also keine Mitarbeiter eingestellt oder entlassen. Ist die Summe $\small{\lt 1}$ fallen Mitarbeiter weg, zum Beispiel durch Entlassungen. Wenn die Summe $\small{\gt 1}$ ist, kommen Mitarbeiter hinzu. Die Firma stellt dann also Mitarbeiter ein.

Vergleichst du die Zahlen der beiden Matrizen kannst du folgende fett markierten Veränderungen feststellen.

		von:	$H$	$F$	$P$
	$H$		$\begin{pmatrix}\boldsymbol{0,8}&0,2&\boldsymbol{0,6}\\[2pt]0,1&0,6&\boldsymbol{0,3}\\[2pt]\boldsymbol{0,1}&0,2&\boldsymbol{0,1}\end{pmatrix}$
nach:	$F$	$B=$
	$P$

Der Eintrag in der ersten Spalte, erste Zeile gibt an, dass sich dieses Jahr $\small{5\%}$ mehr Kunden erneut für einen Hotelurlaub entscheiden.

Der Eintrag in der ersten Spalte dritte Zeile zeigt allerdings, dass nun $\small{5\%}$ weniger der Kunden statt einem Hotelurlaub einen Urlaub in einer Pension buchen.

Eine dritte Veränderung siehst du in der dritten Spalte, erst Zeile. Hier siehst du, dass $\small{3\%}$ der Kunden, die eine Pension gebucht haben, dieses Jahr ein Hotel buchen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?


		von:	$A$	$B$	$C$
	$A$		$\begin{pmatrix}a_{11}&a_{12}&a_{13}\\[2pt] a_{21}&a_{22}&a_{23}\\[2pt]a_{31}&a_{32}&a_{33}\end{pmatrix}$
nach:	$B$	$M=$
	$C$
$a_{11}+a_{21}+a_{31} = 1$
$a_{12}+a_{22}+a_{32} = 1$
$a_{13}+a_{23}+a_{33} = 1$